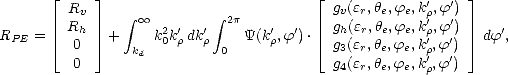
Bien que l’intégrale des coefficients bistatiques donnée en (4.104) et (4.108) soit une solution moins coûteuse en temps de calcul qu’une solution rigoureuse des équations de Maxwell, car elle est issue d’une méthode d’approximation, elle n’en reste pas moins très lourde numériquement. Johnson et Zhang ([45 ]) ont proposé une réécriture de (4.104) et (4.108) qui a l’avantage d’une part d’accélérer considérablement le calcul et d’améliorer la précision, et d’autre part de permettre de mieux apréhender l’influence relative des différentes longueurs d’onde du spectre des vagues dans le processus de diffusion. Le détail du calcule est explicité dans [45], je ne donne dans cette section que les grandes lignes de ce calcul et les résultats importants. En premier lieu, les expressions (4.104) et (4.108) sont rassemblées sous une intégrale unique et RPE s’exprime désormais sous la forme
 | (4.137) |
où les fonctions gv,gh,g3 et g4 sont données par 4.133. Les coefficients de reflexion Ri et Rc donnés en
(4.104) et (4.108) sont très proches en valeur absolue et sont de signe opposé. Ri est positif (augmente la
reflectivité) et Rc est négative. La somme 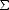 R = Ri + Rc, qui caractérise l’effet total de la diffusion,
résulte donc de la différence
R = Ri + Rc, qui caractérise l’effet total de la diffusion,
résulte donc de la différence  R = |Ri|-|Rc| où |Ri|
R = |Ri|-|Rc| où |Ri|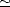 |Rc|. La différence |Ri|-|Rc| va ainsi être faible
devant |Ri | et |Rc|, c’est à dire
|Rc|. La différence |Ri|-|Rc| va ainsi être faible
devant |Ri | et |Rc|, c’est à dire

Ainsi, fixer une précision relative donnée sur l’intégrale numérique de  R est plus efficace que de fixer
cette même précision relative sur les deux intégrales de Ri et Rc effectuée séparement avant de faire la
différence |Ri | -|Rc|.
R est plus efficace que de fixer
cette même précision relative sur les deux intégrales de Ri et Rc effectuée séparement avant de faire la
différence |Ri | -|Rc|.
En developpant les fonctions gv,gh,g3 et g4 en série de fourier de l’angle  ', on peut démontrer ([45]
que R PE s’exprime sous la forme d’une série de Fourier
', on peut démontrer ([45]
que R PE s’exprime sous la forme d’une série de Fourier
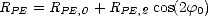 | (4.140) |
où R PE,0 est la réflectivité omnidirectionnelle et RPE,2 est l’amplitude de la variation azimutale de la réflectivité. Ces coefficient sont donnés par les relations suivantes
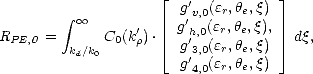 | (4.141) |
et
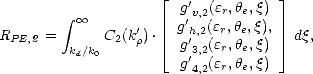 | (4.142) |
où 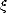 = k
= k '/k0, est le rapport entre la longueur d’onde d’une vague et la longueur d’onde du
radiomètre, C0 (k
'/k0, est le rapport entre la longueur d’onde d’une vague et la longueur d’onde du
radiomètre, C0 (k ') et C2(k
') et C2(k ') sont respectivement le spectre de courbure (C(k
') sont respectivement le spectre de courbure (C(k ',
', ')) omnidirectionnel et
l’amplitude de sa variation azimutale. Ainsi, la composante omnidirectionnelle de la reflectivité des
petites échelles (RPE,0) est obtenue en intégrant sur les échelles comprises entre kd et l’infini le
spectre de courbure omnidirectionnel pondéré par la fonction g'x,0 (où x = v,h,3 ou 4 selon la
polarisation). De même, l’amplitude de la composante azimutale de la reflectivité des petites
échelles (R PE,2 ) est obtenue en intégrant sur les échelles comprises entre kd et l’infini la seconde
harmonique du spectre de courbure pondérée par la fonction g'x,2 (où x = v,h,3 ou 4 selon la
polarisation).
')) omnidirectionnel et
l’amplitude de sa variation azimutale. Ainsi, la composante omnidirectionnelle de la reflectivité des
petites échelles (RPE,0) est obtenue en intégrant sur les échelles comprises entre kd et l’infini le
spectre de courbure omnidirectionnel pondéré par la fonction g'x,0 (où x = v,h,3 ou 4 selon la
polarisation). De même, l’amplitude de la composante azimutale de la reflectivité des petites
échelles (R PE,2 ) est obtenue en intégrant sur les échelles comprises entre kd et l’infini la seconde
harmonique du spectre de courbure pondérée par la fonction g'x,2 (où x = v,h,3 ou 4 selon la
polarisation).
Les fonctions de poids g'x,0,, sont illustrées sur les figures 4.22, 4.23 et 4.24 respectivement pour
des incidence de 0o, 30o et 60o. On peut déduire de ces figures qu’au nadir (figure 4.22),
la réflectivité d’une surface rugueuse (PE) est essentiellement affectée par les vagues dont
la longueur d’onde est de l’ordre de  0. Lorsque l’incidence augmente (figures 4.22, 4.23 et
4.24), la gamme des longueurs d’ondes affectant sensiblement la réflectivité s’élargie autour de
0. Lorsque l’incidence augmente (figures 4.22, 4.23 et
4.24), la gamme des longueurs d’ondes affectant sensiblement la réflectivité s’élargie autour de
 0 .
0 .
|
|
|
|