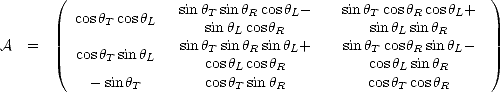) et d’azimuth (
) et d’azimuth ( ) pour chaque mesure
de T b . On peut ainsi estimer la Tb théorique à partir du modèle d’émissivité (voir chapitre
4).
) pour chaque mesure
de T b . On peut ainsi estimer la Tb théorique à partir du modèle d’émissivité (voir chapitre
4).
|
|
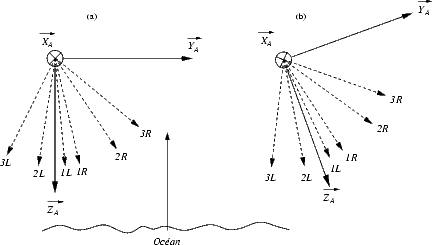
La direction de visée des antennes par rapport à la surface de la mer est illustrée sur la figure 7.13 dans le cas d’un avion en position horizontale (a) et dans le cas d’un avion incliné (b). Sur la figure, l’avion n’est incliné que dans le plan (O;
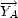 ;
;
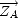 )
mais il peut bien sûr subir une rotation dans n’importe quel plan. On va calculer
)
mais il peut bien sûr subir une rotation dans n’importe quel plan. On va calculer  et
et  à partir de
à partir de  A
et
A
et  A , qui sont les coordonnées de l’antenne dans le repère de l’avion, et des coordonnées
d’attitude de l’avion qui sont l’angle de roulis (
A , qui sont les coordonnées de l’antenne dans le repère de l’avion, et des coordonnées
d’attitude de l’avion qui sont l’angle de roulis ( R), de tangage (
R), de tangage ( T) et de lacet (
T) et de lacet ( L). Par
convention (la convention RTL), le changement de repère entre un avion en position horizontale et
un avion incliné s’effectue en appliquant successivement et dans l’ordre les trois rotations
suivantes:
L). Par
convention (la convention RTL), le changement de repère entre un avion en position horizontale et
un avion incliné s’effectue en appliquant successivement et dans l’ordre les trois rotations
suivantes:
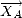 ,
qui transforme les axes
,
qui transforme les axes
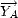 et
et
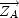 en
en
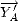 et
et
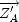 ;
;
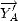 ,
qui transforme les axes
,
qui transforme les axes
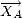 et
et
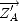 en
en
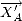 et
et
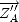 ;
;
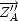 ,
qui transforme les axes
,
qui transforme les axes
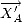 et
et
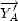 en
en
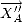 et
et
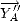 .
.
On va écrire les matrices de ces trois rotations. Les rotations sont définies dans le sens trigonométrique autour des trois axes d’un repère orthonormé. L’axe
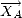 représente l’axe longitudinal de l’avion dans la direction de vol, l’axe
représente l’axe longitudinal de l’avion dans la direction de vol, l’axe
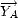 est transversal à l’avion
(le long des ailes) et l’axe
est transversal à l’avion
(le long des ailes) et l’axe
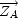 est l’aplomb, dirigé vers le bas de sorte qu’un tangage de signe positif lève le nez de l’avion au dessus de
l’horizon (voir figure 7.5).
est l’aplomb, dirigé vers le bas de sorte qu’un tangage de signe positif lève le nez de l’avion au dessus de
l’horizon (voir figure 7.5).
On écrit la matrice AR, rotation de roulis autour de
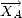 ,
,
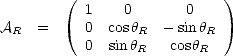
Ainsi, un vecteur quelconque,
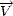 , qui
subit une rotation d’angle
, qui
subit une rotation d’angle  R autour de
R autour de
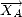 s’écrira
s’écrira
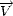 ' =
AR .
' =
AR .
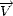 dans la
base (
dans la
base (
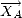 ,
,
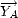 ,
,
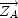 ). On a de même la matrice
AT rotation autour de
). On a de même la matrice
AT rotation autour de
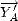 ,
,
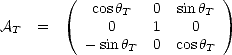
et la matrice AL rotation autour de
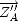 ,
,
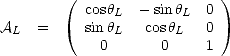
On utilise la convention RTL, qui impose d’appliquer dans l’ordre la rotation  R de roulis (autour de
R de roulis (autour de
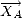 ), la rotation
), la rotation  T de tangage
(autour de
T de tangage
(autour de
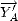 ) et enfin la rotation
) et enfin la rotation
 L de lacet (autour de
L de lacet (autour de
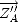 ).
).
On détermine ainsi la matrice A = AL ×AT ×AR,