Next: 3.2 Instrumentation
Up: 3. Le théorème de
Previous: 3. Le théorème de
Quelque soit la géométrie du réseau d'antenne d'un
radiomètre imageur à synthèse d'ouverture, le dispositif
élémentaire est formé par un couple d'antennes dont la
corrélation des signaux va fournir une mesure du degré de
cohérence spatiale à la fréquence angulaire déterminée par
la distance entre les antennes. La démonstration suivante,
qui dans un premier temps ne fait pas intervenir les
caractéristiques instrumentales, permet d'établir, pour ce
couple d'antenne, le théorème de VAN CITTERT-ZERNIKE reliant la visibilité 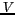 à la distribution
spatiale d'intensité
à la distribution
spatiale d'intensité  .
.
Le champ électromagnétique résultant de la présence d'une
distribution de charge alternative 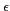 placée en
placée en
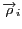 est mesurée par une antenne placée
en
est mesurée par une antenne placée
en
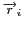 (voir Fig. 3.1). Sous les
hypothèses suivantes :
(voir Fig. 3.1). Sous les
hypothèses suivantes :
- la polarisation du champ est ignorée : le champ
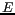 est considéré comme une quantité scalaire (cette
supposition n'est pas nécessaire mais rend la démonstration
plus claire),
est considéré comme une quantité scalaire (cette
supposition n'est pas nécessaire mais rend la démonstration
plus claire),
- le champ résulte uniquement d'une distribution
surfacique de charges,
- le principe de Huygens est appliqué
(l'amplitude du champ varie en
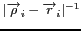 et
sa phase dépend du chemin parcouru de la source à la réception),
et
sa phase dépend du chemin parcouru de la source à la réception),
le champ 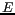 mesuré en
mesuré en
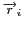 est de la forme :
est de la forme :
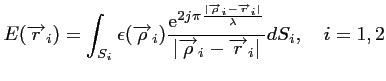 |
(3.1) |
La corrélation des champs mesurés en
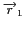 et
et
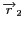 est alors :
est alors :
La source est supposée spatialement incohérente, ce qui
implique que
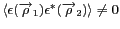 uniquement pour
uniquement pour
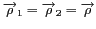 , soit :
, soit :
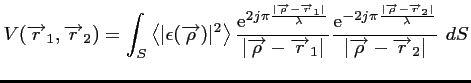 |
(3.4) |
La géométrie du dispositif étudié, illustré par la figure
![[*]](file:///C|/texutils/l2h/icons/crossref.gif) , permet d'établir les relations suivantes :
, permet d'établir les relations suivantes :
Or, la distance à la source est beaucoup plus grande que la
distance entre les antennes,
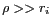 :
:
ce qui conduit à :
et à :
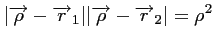 |
(3.9) |
En remarquant que
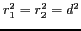 , l'expression 3.8 se simplifie
:
, l'expression 3.8 se simplifie
:
Il reste alors à exprimer les deux produits scalaires :
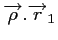 |
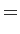 |
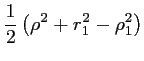 |
(3.11) |
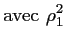 |
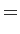 |
![$\displaystyle H^2 \left[1+\frac{(x+d_1/2)^2}{H^2}+\frac{(d_2/2-y)^2}{H^2} \right]$](img400.gif) |
(3.12) |
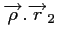 |
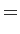 |
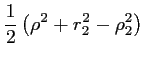 |
(3.13) |
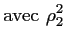 |
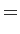 |
![$\displaystyle H^2 \left[1+\frac{(x-d_1/2)^2}{H^2}+\frac{(d_2/2+y)^2}{H^2} \right]$](img404.gif) |
(3.14) |
ce qui conduit à :
Le report des deux résultats 3.17 et 3.9
dans la relation 3.4 conduit à l'expression suivante de
la corrélation des champs reçus par les deux antennes :
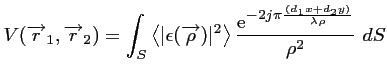 |
(3.17) |
Les définitions suivantes sont introduites :
fréquences spatiales angulaires, ligne de base, cosinus
directeurs
- les quantités
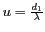 et
et
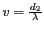 sont des fréquences spatiales
angulaires, avec
sont des fréquences spatiales
angulaires, avec 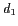 et
et 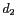 les projections
du vecteur liant les deux antennes sur les axes du
référentiel attaché à l'instrument et
les projections
du vecteur liant les deux antennes sur les axes du
référentiel attaché à l'instrument et 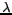 la longueur
d''onde d'observation
la longueur
d''onde d'observation
- le couple 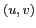 est appelé ligne de
base
est appelé ligne de
base
-
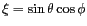 et
et
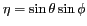 sont appelés cosinus directeurs En introduisant
sont appelés cosinus directeurs En introduisant
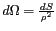 , la relation 3.18
conduit au théorème de VAN CITTERT-ZERNIKEVanC1VanC2Zern
liant la distribution spatiale d'intensité
, la relation 3.18
conduit au théorème de VAN CITTERT-ZERNIKEVanC1VanC2Zern
liant la distribution spatiale d'intensité
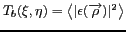 à la
valeur du degré de cohérence spatiale à la fréquence
à la
valeur du degré de cohérence spatiale à la fréquence 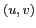 :
:
Ainsi, en négligeant tous les aspects
instrumentaux, la corrélation des signaux reçus par deux
antennes ayant un champ de vue se recouvrant, fournit une
mesure la transformée de Fourier à la fréquence 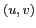 de
la quantité
de
la quantité
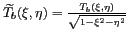 appelée température de brillance modifiée. La section
suivante va montrer comment les caractéristiques
instrumentales vont venir modifier cette expression.
appelée température de brillance modifiée. La section
suivante va montrer comment les caractéristiques
instrumentales vont venir modifier cette expression.
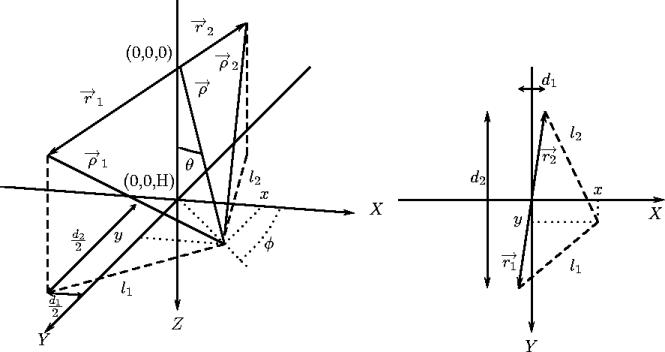
Figure 3.1: Description du référentiel lié
à un couple d'antenne. L'origine est située à mi-distance de
deux antennes placées à l'extrémité des vecteurs
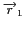 et
et
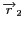 . La projection de
. La projection de
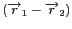 sur l'axe
sur l'axe 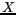 est notée
est notée 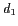 , celle sur l'axe
, celle sur l'axe 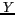 ,
, 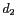 . Les antennes observent une distribution surfacique
. Les antennes observent une distribution surfacique 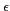 sur le plan
sur le plan 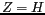 (projection sur ce plan à droite). Les coordonnées d'un
point de ce plan sont notées
(projection sur ce plan à droite). Les coordonnées d'un
point de ce plan sont notées 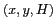 ou
ou
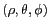 .
.




Next: 3.2 Instrumentation
Up: 3. Le théorème de
Previous: 3. Le théorème de
nous
2005-03-31
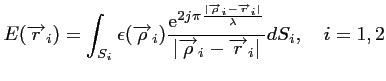
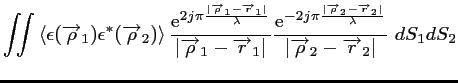
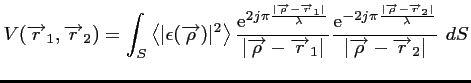
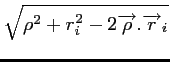
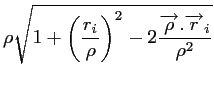
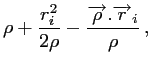
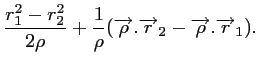
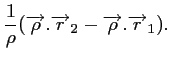
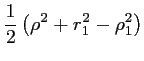
![$\displaystyle H^2 \left[1+\frac{(x+d_1/2)^2}{H^2}+\frac{(d_2/2-y)^2}{H^2} \right]$](img400.gif)
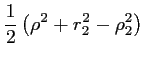
![$\displaystyle H^2 \left[1+\frac{(x-d_1/2)^2}{H^2}+\frac{(d_2/2+y)^2}{H^2} \right]$](img404.gif)
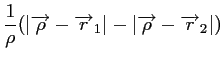
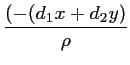
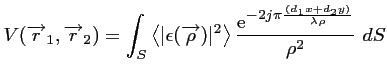
 e
e e
e