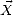 et
et 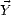 reliés par la matrice A de sorte que
reliés par la matrice A de sorte que
Si l’on a deux vecteurs colonne 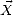 et
et 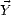 reliés par la matrice A de sorte que
reliés par la matrice A de sorte que
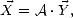 | (N.114) |
alors
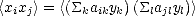 | (N.115) |
où xi et xj sont les éléments respectivement des lignes i et j du vecteur 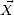 , yk et yl sont les éléments
respectivement des lignes k et l du vecteur
, yk et yl sont les éléments
respectivement des lignes k et l du vecteur 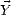 , et aik et ajl sont les éléments respectivement de la ligne i,
colonne k et de la ligne j, colonne l de la matrice A. On a alors
, et aik et ajl sont les éléments respectivement de la ligne i,
colonne k et de la ligne j, colonne l de la matrice A. On a alors
![<xixj> = <SkSlaikajlykyl> (N.116)
= SkSlaikajl<ykyl> (N.117)
= A[<y y>]At, (N.118)
k l](plan_html981x.gif)
d’où, si C est la matrice de covariance des x et 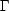 est la matrice de covariance des y,
est la matrice de covariance des y,
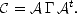 | (N.119) |