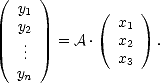
Soit le système linéaire
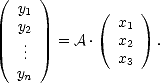 | (O.120) |
où les y1 , y2 , ..., yn sont les mesures, qui sont des variables aléatoires indépendantes et normalisées de sorte que toutes les variances soient égales à 1. Les inconnues sont x1, x2 et x3. Pour résoudre le système,
 12,
12,  22,
22,  32 et ses trois vecteurs propres normés
32 et ses trois vecteurs propres normés
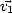 ,
, 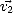 ,
, 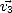 ,
,
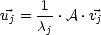
On déduit la matrice U (34 lignes x 3 colonnes), constituée des trois vecteurs colonnes 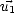 ,
, 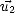 ,
, 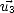 , et
la matrice V (3 lignes x 3 colonnes), constituée des trois vecteurs colonnes
, et
la matrice V (3 lignes x 3 colonnes), constituée des trois vecteurs colonnes 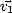 ,
,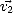 ,
,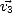 . On a
alors
. On a
alors
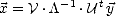 | (O.121) |
où
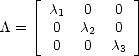 | (O.122) |
et donc
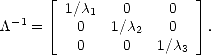 | (O.123) |
Pour calculer l’erreur sur la 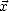 , on écrit
, on écrit
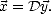 | (O.124) |
On a alors, d’après (N.119), la matrice de covariance de 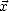 suivante
suivante
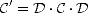
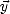 et Id est la matrice identité. On a, d’après (O.121),
et Id est la matrice identité. On a, d’après (O.121),
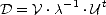
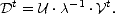
Comme U . Ut = Id, on obtient
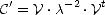
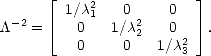 | (O.125) |