La résolution spatiale est une contrainte forte pour la mesure de la SSS et surtout pour la mesure de l’humidité des sols. Elle doit être de l’ordre de 100 km pour que la mesure de la SSS soit utile aux océanographes (voir les recommendation GODAE dans la section 1.2).
La résolution spatiale d’une antenne réelle, de taille fixée, est d’autant plus dégradée que sa fréquence
 0 est basse. En effet, la résolution angulaire
0 est basse. En effet, la résolution angulaire 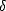
 d’une antenne (cette résolution est liée à la figure de
diffraction de l’ouverture de l’antenne) est donnée par
d’une antenne (cette résolution est liée à la figure de
diffraction de l’ouverture de l’antenne) est donnée par
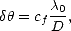
 0 = c/
0 = c/ 0 est la longueur d’onde de l’antenne, D est sa taille et cf est un coefficient qui dépend de la
forme de l’antenne ([48, 90]). La résolution au sol
0 est la longueur d’onde de l’antenne, D est sa taille et cf est un coefficient qui dépend de la
forme de l’antenne ([48, 90]). La résolution au sol 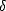 x se déduit de
x se déduit de 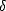
 , pour une visée au nadir,
par
, pour une visée au nadir,
par
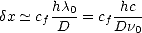
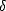
 est petit de sorte que sin
est petit de sorte que sin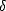

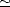
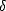
 et que la courbure de la Terre soit
négligeable. On a vu dans la section 2.2, que la sensibilité de la Tbmer à la SSS est d’autant plus forte que
la fréquence est basse. Mais plus
et que la courbure de la Terre soit
négligeable. On a vu dans la section 2.2, que la sensibilité de la Tbmer à la SSS est d’autant plus forte que
la fréquence est basse. Mais plus  0 est basse, à taille d’antenne fixée, plus la résolution est
médiocre. La taille d’une antenne est un problème important à la fréquence de 1.41 GHz (i.e.
0 est basse, à taille d’antenne fixée, plus la résolution est
médiocre. La taille d’une antenne est un problème important à la fréquence de 1.41 GHz (i.e.
 0 = 0.21 m). À cette fréquence, une résolution spatiale de 30 km à une altitude h = 750 km
nécessiterait une taille d’antenne de plus de 5 m. Une telle antenne serait difficilement déployable
dans l’espace. C’est pour résoudre ce problème que MIRAS utilise la technique de synthèse
d’ouverture.
0 = 0.21 m). À cette fréquence, une résolution spatiale de 30 km à une altitude h = 750 km
nécessiterait une taille d’antenne de plus de 5 m. Une telle antenne serait difficilement déployable
dans l’espace. C’est pour résoudre ce problème que MIRAS utilise la technique de synthèse
d’ouverture.
Une antenne à synthèse d’ouverture est constituée d’un réseau d’antennes élémentaires, dont les mesures sont combinées de manière cohérente par interférométrie (i.e. en prenant en compte la phase relative des différents signaux mesurés, [48, 90]). La résolution angulaire de l’antenne à synthèse d’ouverture ainsi obtenue atteint celle qu’aurait une antenne à ouverture réelle dont la taille serait égale à la distance maximale entre deux antennes élémentaires. En d’autres termes, alors que dans les conditions précédemment citées une antenne réelle devait mesurer 5 m pour obtenir une résolution spatiale de 30 km, une antenne à synthèse d’ouverture atteint la même résolution à partir de deux antennes élémentaires distantes de 5 m. Une telle antenne est donc plus facile a deployer dans l’espace car les antennes élémentaires peuvent être très petites. MIRAS sera equipé de trois bras d’une longueur de 4 m, disposés en forme de Y, composés chacun de trois sections pliables aisément embarquable dans une fusée. Une fois dans l’espace, les bras se déplieront comme cela est illustré par exemple sur la figure 3.3. Les antennes élémentaires n’étant pas alignées, MIRAS sera un interféromètre à deux dimensions (le premier a être utilisé depuis l’espace) produisant des images de la surface de la Terre. Chacun des bras du Y porte 18 antennes élementaires (6 par section), et 18 antennes élémentaires supplémentaires sont disposées sur le support (hub) des bras (voir la figure 3.2).
La contrepartie de la diminuation de la taille de l’antenne, apportée par la technique de la synthèse
d’ouverture, est que la précision (ou résolution) radiométrique sera d’autant plus dégradée que la
surface collectrice réelle de l’antenne sera petite. La précision radiométrique d’une mesure
élémentaire de MIRAS ( T) est donnée approximativement par (note technique, Waldteufel
(1999))
T) est donnée approximativement par (note technique, Waldteufel
(1999))
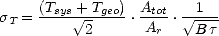 | (3.1) |
où
 r2 est la surface du disque (de rayon r = 4 m) contenant les antennes élémentaires de
l’instrument,
r2 est la surface du disque (de rayon r = 4 m) contenant les antennes élémentaires de
l’instrument,
 est le temps d’integration de la mesure (s).
est le temps d’integration de la mesure (s).Ar est donné par l’expression
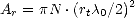 | (3.2) |
où N est le nombre d’antennes élémentaires et (rt 0/2)2 est la surface d’une antenne élémentaire, avec
rt = 0.88 et
0/2)2 est la surface d’une antenne élémentaire, avec
rt = 0.88 et  0 = 0.21 m. S’il on fixe N = 72, B = 19 MHz,
0 = 0.21 m. S’il on fixe N = 72, B = 19 MHz,  = 1.5 s pour chaque polarisation, on obtient
une précision radiométrique de l’ordre du Kelvin (0.8 à 1.14 K pour Tgeo variant de 50 K à 150 K). Cette
estimation s’applique aux visées proches de l’axe de l’antenne ; sur les marges du FOV, elle peut être
détériorée par un facteur allant jusqu’à 2.5, par suite de l’effet du diagramme de rayonnement des
antennes élémentaires de l’interféromètre.
= 1.5 s pour chaque polarisation, on obtient
une précision radiométrique de l’ordre du Kelvin (0.8 à 1.14 K pour Tgeo variant de 50 K à 150 K). Cette
estimation s’applique aux visées proches de l’axe de l’antenne ; sur les marges du FOV, elle peut être
détériorée par un facteur allant jusqu’à 2.5, par suite de l’effet du diagramme de rayonnement des
antennes élémentaires de l’interféromètre.