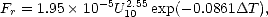
 T
([60 ]). Je vais décrire dans cette section deux modèles que j’ai utilisés pour estimer l’effet
de l’écume sur Tbmer en bande L. Plusieurs modèles ont été proposés, essentiellement par
Monahan et ses collaborateurs, indiquant une variation de Fr avec U selon une loi de puissance,
dont la puissance varie de 2.5 à 3.5. Le taux de couverture déduit du modèle proposé par
Monahan et O’Muircheartaigh ([62]), qui relie Fr au vent à 10 mètres de hauteur U10 et à
T
([60 ]). Je vais décrire dans cette section deux modèles que j’ai utilisés pour estimer l’effet
de l’écume sur Tbmer en bande L. Plusieurs modèles ont été proposés, essentiellement par
Monahan et ses collaborateurs, indiquant une variation de Fr avec U selon une loi de puissance,
dont la puissance varie de 2.5 à 3.5. Le taux de couverture déduit du modèle proposé par
Monahan et O’Muircheartaigh ([62]), qui relie Fr au vent à 10 mètres de hauteur U10 et à  T
par
T
par
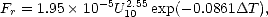 | (4.145) |
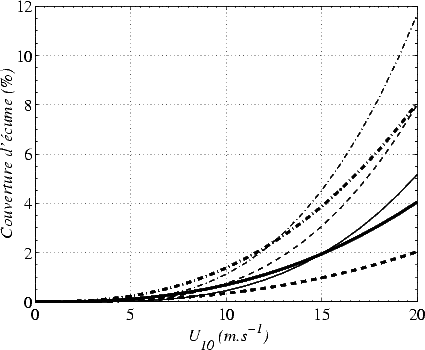
est illustré sur la figure 4.25.
|
|
Pour qu’il y ait formation d’écume sur la surface océanique, il faut qu’il y ait un vent supérieur à un
certain seuil. Munk ([64]) a estimé ce vent minimum UB (pour vent de Beaufort) comme étant de 7
m.s-1 . Monahan et O’Muircheartaigh ont montré, à partir d’un large ensemble de photographies,
provenant de cinq campagnes effectuées dans des régions où règnent des conditions géophysiques
variées9 ,
qu’en réalité UB dépend de  T et de la SST.
T et de la SST.
Pour les atmosphères très stables (i.e.  T = 8oC), UB est effectivement de l’ordre de
7 m.s-1 alors que pour les atmosphères instables (i.e.
T = 8oC), UB est effectivement de l’ordre de
7 m.s-1 alors que pour les atmosphères instables (i.e.  T = -4oC) UB est de l’ordre de 2
m.s-1 . Il y a donc une forte variabilité de UB (ainsi que de Fr) avec
T = -4oC) UB est de l’ordre de 2
m.s-1 . Il y a donc une forte variabilité de UB (ainsi que de Fr) avec  T; cependant, une
large majorité des 305 observations utilisées par Monahan et O’Muircheartaigh indique une
atmosphère neutre, voir une atmosphère légèrement instable (i.e. -2oC<
T; cependant, une
large majorité des 305 observations utilisées par Monahan et O’Muircheartaigh indique une
atmosphère neutre, voir une atmosphère légèrement instable (i.e. -2oC<  T < 0oC ) ([62]),
les cas où
T < 0oC ) ([62]),
les cas où  T > 0oC ou
T > 0oC ou  T < -2oC étant peu fréquents. La stabilité mesurée pendant la
campagne WISE 2000 (voir la figure 7.29) est en accord avec ces observations indiquant un
T < -2oC étant peu fréquents. La stabilité mesurée pendant la
campagne WISE 2000 (voir la figure 7.29) est en accord avec ces observations indiquant un
 T moyen de l’ordre de -1oC et un écart type de l’ordre de 1oC. Bien que l’ensemble de ces
observations ne soit pas statistiquement représentatif de l’océan global, il donne un ordre de
grandeur de la variabilité de
T moyen de l’ordre de -1oC et un écart type de l’ordre de 1oC. Bien que l’ensemble de ces
observations ne soit pas statistiquement représentatif de l’océan global, il donne un ordre de
grandeur de la variabilité de  T qui est faible. Je vais desormais supposer que l’atmosphère est
neutre.
T qui est faible. Je vais desormais supposer que l’atmosphère est
neutre.
Pour une atmosphère neutre (i.e.  T = 0oC), UB et Fr varient sensiblement avec la SST. UB varie de
3.4 m.s-1 à 2.7 m.s-1 pour une SST variant de 0oC à 30oC ([62]). La variation de Fr avec la SST est
illustrée sur la figure 4.25 d’après le modèle de Monahan et Lu [60]. Ce modèle fait la distinction entre
deux types d’écume (voir aussi [17]):
T = 0oC), UB et Fr varient sensiblement avec la SST. UB varie de
3.4 m.s-1 à 2.7 m.s-1 pour une SST variant de 0oC à 30oC ([62]). La variation de Fr avec la SST est
illustrée sur la figure 4.25 d’après le modèle de Monahan et Lu [60]. Ce modèle fait la distinction entre
deux types d’écume (voir aussi [17]):
L’écume de type A a une étendue spatiale plus faible que celle de type B, elle va plus profondement dans la mer (jusqu’à 50 cm contre quelques centimètres pour le type B), elle existe moins longtemps (de l’ordre de la seconde contre quelques minutes/heures pour le type B), ses bulles sont plus grandes et elle contient plus d’eau ([75, 60, 17]). D’après le modèle de Monahan et Lu, le taux de couverture d’écume de type A est donné par
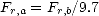 | (4.146) |
et celui de type B par
![[ ]
Fr,b = 5.21 ×10- 4 .(U (gn)-1/3 -75.9)3](plan_html365x.gif) | (4.147) |
avec g l’accélération de la pesanteur et  la viscosité cinématique de l’eau de mer donnée
par
la viscosité cinématique de l’eau de mer donnée
par
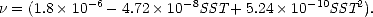 | (4.148) |
Bien que le taux d’écume tracé sur la figure 4.25 soit le taux d’écume total, qui prend en compte les deux types d’écume, il est probable que ces deux types d’écume interagissent différemment avec les ondes EM ([66 , 60 ]) et que le taux total surestime la portion de l’écume qui influence sensiblement Tbmer.
Il existe d’autres modèles de couverture d’écume ([100, 61]) prédisant des résultats supérieurs à ceux présentés ici, particulièrement pour les vents forts ([6]). Pourtant, quel que soit le modèle utilisé, le taux de couverture d’écume est faible (moins de 5%) pour des vents inférieurs à 15 m.s-1, et même très faible (moins de 1%) pour des vents inférieurs au vent moyen (U = 8 m.s-1) à la surface du globe. Ce taux varie exponentiellement avec le vent et cette variation est très sensible à la SST et à la stabilité (je supposerai que la stabilité est nulle par la suite).
Les deux modèles de couverture d’écume sont relativement proches et ne diffèrent que de quelques pourcents, surtout pour des vents modérés. L’importance de ces quelques pourcents d’écart entre les modèles pour l’incertitude sur l’effet de l’écume (qui a été étudiée par Boutin et al., [6]), de même que l’influence de la couverture d’écume sur Tbmer, vont dépendre de l’émissivité de l’écume. Les modèles de couverture d’écume discutés dans cette section ont été établis pour une mer pleinement développée. Il ne sont probablement pas applicables près des côtes où le taux d’écume décroît à cause du fetch limité, d’après les observations radiométriques de Webster et al. ([94]). J’ai comparé le modèle de Monahan et Lu avec des mesures de taux de couverture effectuées dans une zone de fetch limité (voir la section 7.3). Le taux de couverture mesuré était sensiblement plus faible que celui prédit par le modèle.