|
|
|

|
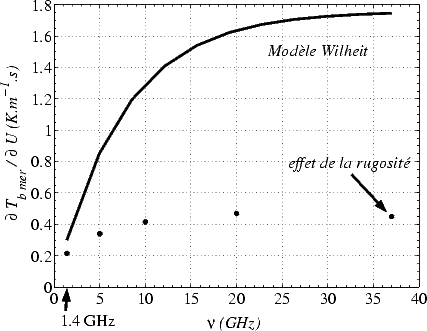
La figure 4.26 illustre la variation avec la fréquence de l’influence de l’écume sur Tbmer d’après le
modèle proposé par Wilheit ([97]) et pour une SST de 20oC. Ce modèle a été dérivé empiriquement pour
ajuster des mesures radiométriques à 1.42 GHz, 4.99 GHz, 10.69 GHz, 19.35 GHz, 31.4 GHz et 37 GHz
([94 ]). L’accroissement d’émissivité de la surface océanique  e en fonction du vent U et de la fréquence
e en fonction du vent U et de la fréquence  est donné par la loi
est donné par la loi
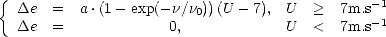 | (4.149) |
Le problème avec l’approche de Wilheit est de séparer les différents effets du vent sur Tbmer, c’est à dire de séparer les effets dûs à l’écume d’une part et ceux dûs à la rugosité de la surface océanique d’autre part. Pour Wilheit (ainsi que pour Nordberg et al., [66] et Stogryn, [84]) l’effet de la rugosité sur Tbmer est supposé être nul au nadir, ce qui le conduit à conclure que l’incrément de Tbmer avec le vent au nadir est dû uniquement (ou essentiellement) à l’écume. Cette hypothèse repose sur les résultats du modèle d’émissivité de la mer proposé par Stogryn ([83]) qui utilise une approche d’optique géométrique telle que celle décrite dans la section 4.4 et qui, par conséquent, ne prédit aucune influence de la rugosité de surface sur Tbmer au nadir. J’ai reporté sur la figure 4.26 la contribution de la rugosité à l’influence du vent sur Tbmer, que j’ai estimée avec un modèle d’émissivité à deux-échelles (modèle de spectre DV2) pour différentes fréquences. S’il est vrai qu’à haute fréquence le signal est essentiellement dû à l’écume, en bande L la contribution majeure provient de la rugosité. Par conséquent, l’effet de l’écume est certainement très surévalué par le modèle de Wilheit. Une fois retiré l’effet de la rugosité sur le signal, l’effet de l’écume serait de 0.1 K.m-1.s ; il est possible que cet effet residuel soit lié à des imprécisions de mesure sur les données utilisées par Wilheit et/ou à sous-estimation de l’amplitude du spectre, dans le modèle que j’ai utilisé, qui reviendrait à sous-estimer l’effet de la rugosité (voir les comparaisons avec des mesures dans la section 7.3).
Pour évaluer Tbec. en bande L, j’ai utilisé, comme dans [102], le modèle d’émissivité de l’écume de
Stogryn ([84 ]) bien que celui-ci n’ait été validé qu’entre 13.4 GHz et 37 GHz. Le modèle de Stogryn est un
modèle empirique de température de brillance basé sur des mesures de Tb. Des lois reliant Tb à
la fréquence  et à l’angle d’incidence
et à l’angle d’incidence  sont déduites par regression sur les mesures. On a
ainsi
sont déduites par regression sur les mesures. On a
ainsi
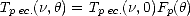 | (4.150) |
où p = v ou h est respectivement pour les V- et H-pol,
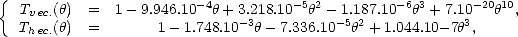
et
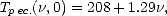 | (4.151) |
avec  en radians et
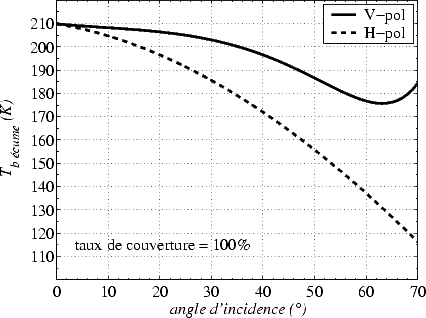
en radians et  en GHz. La température de brillance de l’écume en bande L prédite par le
modèle de Stogryn est illustrée sur la figure 4.27. Elle est très supérieure à Tbmer (qui est de l’ordre de
100 au nadir, voir la section 4.6) et même si l’écume représente une petite fraction de surface océanique,
son effet sur T bmer risque d’être sensible.
en GHz. La température de brillance de l’écume en bande L prédite par le
modèle de Stogryn est illustrée sur la figure 4.27. Elle est très supérieure à Tbmer (qui est de l’ordre de
100 au nadir, voir la section 4.6) et même si l’écume représente une petite fraction de surface océanique,
son effet sur T bmer risque d’être sensible.
|
|
Outre le problème lié au fait que le modèle de Stogryn soit développé pour des fréquences sensiblement plus élevées que 1.41 GHz, ce modèle suppose que l’écume a une épaisseur infinie. Or on conçoit que l’interaction d’une onde EM avec le milieu écume va dépendre sensiblement de l’épaisseur de ce milieu, du moins tant que cette épaisseur est inférieure à l’épaisseur de peau. Droppleman ([25]) a montré que plus la longueur d’onde est grande devant l’épaisseur d’écume, plus l’émissivité de l’écume est faible. De plus, Tbec.prédite par le modèle de Stogryn ne dépend ni de la SST ni de la fraction d’air contenue dans l’écume.
J’ai comparé le modèle de Droppleman ([25]), qui propose une relation pour la constante diélectrique de l’écume basée sur un modèle de mélange air-eau, au modèle de Stogryn. La constante diélectrique de l’écume est donnée par
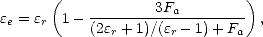 | (4.152) |
où Fa est la fraction de volume d’air dans un volume d’écume. La fraction d’air dans l’écume de type
B est de l’ordre de 90% (celle dans l’écume de type A est beaucoup plus faible, de l’ordre de 50
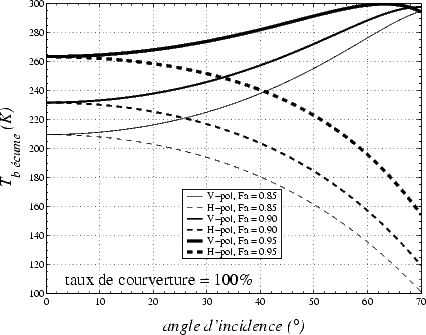
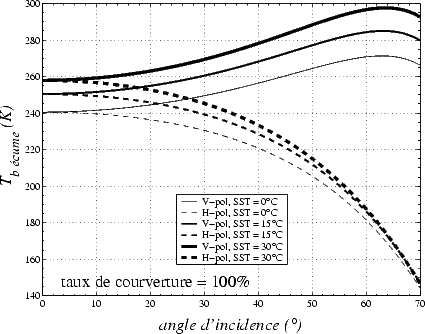
%). La figure 4.28 illustre Tbec. prédite par le modèle de Droppleman pour différentes Fa et
la figure 4.29 T bec. pour différentes SST. Plus la fraction d’air est importante, plus Tbec.
est grande. On remarque que la variation de Tbec. avec  en polarisation verticale est très
différente entre les modèles de Droppleman et de Stogryn, mais comparable en H-pol pour
Fa = 0.85.
en polarisation verticale est très
différente entre les modèles de Droppleman et de Stogryn, mais comparable en H-pol pour
Fa = 0.85.
|
|
|
|
Si l’on prend en compte l’épaisseur de la couche d’écume relativement à la longueur d’onde, il est probable que l’influence de l’écume soit plus faible en bande L qu’à plus haute fréquence où l’effet de l’écume est très sensible. Boutin et al. ([6]) ont estimé, à partir du modèle de Droppleman, Tbec. au nadir pour des épaisseurs d’écume de 1 cm et de 2 cm à respectivement 209 K et 233 K ( à SST = 15o C et Fa = 0.95), ce qui est respectivement inférieur de 41 K et 17 K à Tbec. pour une épaisseur infinie. Par conséquent, les valeurs illustrées sur les figures 4.28 et 4.29 majorent T bec. en bande L. L’effet de l’écume sur Tbmer est discuté dans les sections 4.6 et 7.3.