
 , la même brillance que la mer. Un corps noir est
un objet qui absorbe tout le rayonnement incident à sa surface, et par conséquent dont la
réflectivité est nulle. Sa brillance spectrale B
, la même brillance que la mer. Un corps noir est
un objet qui absorbe tout le rayonnement incident à sa surface, et par conséquent dont la
réflectivité est nulle. Sa brillance spectrale B cn (i.e. la brillance par unité de fréquence, en
Wsr-1 m-2 Hz -1) à la fréquence
cn (i.e. la brillance par unité de fréquence, en
Wsr-1 m-2 Hz -1) à la fréquence  lorsqu’il est à la température T est donnée par la loi de
Planck
lorsqu’il est à la température T est donnée par la loi de
Planck
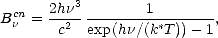 | (2.11) |
où c = 2.997925 × 108 m.s-1 est la vitesse de la lumière dans le vide, h 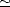 6.62 × 10-34 est la constante
de Planck et k*
6.62 × 10-34 est la constante
de Planck et k* 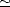 1.38 × 10-23JK-1 est la constante de Boltzmann. Dans le domaine de fréquences qui
nous intéresse, h
1.38 × 10-23JK-1 est la constante de Boltzmann. Dans le domaine de fréquences qui
nous intéresse, h « kT, aussi on utilise l’approximation basses fréquences de Rayleigh-Jeans qui
conduit à l’expression suivante pour la brillance d’un corps noir dans une bande de fréquence
« kT, aussi on utilise l’approximation basses fréquences de Rayleigh-Jeans qui
conduit à l’expression suivante pour la brillance d’un corps noir dans une bande de fréquence


|
|
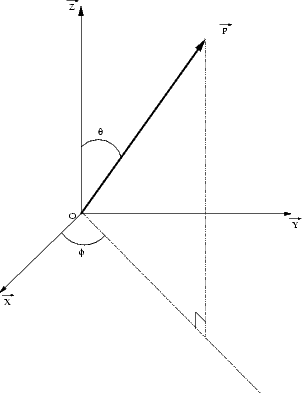
La brillance de la mer n’est pas isotrope et sa variation avec la direction ( ,
, ) (voir la figure 2.1
pour la définition des angles) va dépendre de la structure de la surface de la mer. Ainsi, la
brillance de la mer dans une bande de fréquence
) (voir la figure 2.1
pour la définition des angles) va dépendre de la structure de la surface de la mer. Ainsi, la
brillance de la mer dans une bande de fréquence 
 et dans la direction (
et dans la direction ( ,
, ) est donnée
par
) est donnée
par
On a ainsi la définition de la Tb d’après (2.13) et (2.14) qui conduisent à
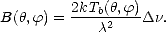 | (2.15) |
Un corps noir (dont la Tb est par définition sa température physique) à l’équilibre thermodynamique est le corps qui émet le plus d’énergie ; la Tb d’un milieu est donc au plus égale à sa température physique (la SST pour le cas de la surface océanique). On définit alors l’émissivité e du milieu comme le rapport entre la brillance du milieu et celle d’un corps noir à la même température que le milieu. On déduit ainsi de (2.15) que l’émissivité de l’océan vaut
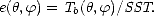 | (2.16) |
Une grande partie de ma thèse a porté sur la modélisation de la température de brillance de la mer en
fonction de plusieurs paramètres géophysiques (voir chapitre 4). Cependant, un radiomètre ne mesure pas
directement la Tb d’une cible, mais une température d’antenne (TA), qui est définie comme la
température à laquelle une résistance délivrerait au récepteur de sortie une puissance de bruit thermique
identique à celle délivrée par l’antenne. Pour relier la TA à la Tb, on va distinguer deux étapes dans les
processus qui conduisent de la puissance émise par la mer à la puissance mesurée par l’antenne
(voir figure 2.2). Le premier processus à considérer est que plusieurs sources émettent vers
l’instrument à partir de directions ( a,
a, a) différentes, et que l’océan n’est que l’une d’entre
elles (voir chapitre 6). Ces différents rayonnements vont traverser un milieu susceptible de
les modifier, l’atmosphère terrestre, avant d’atteindre l’antenne. À l’entrée de l’antenne, on
a donc pour toutes les directions (
a) différentes, et que l’océan n’est que l’une d’entre
elles (voir chapitre 6). Ces différents rayonnements vont traverser un milieu susceptible de
les modifier, l’atmosphère terrestre, avant d’atteindre l’antenne. À l’entrée de l’antenne, on
a donc pour toutes les directions ( a,
a, a) des ”températures apparentes”, TAp(
a) des ”températures apparentes”, TAp( a,
a, a), qui
vont toutes contribuer plus ou moins à la TA. Le deuxième processus à considérer est que
l’antenne est directive, c’est à dire que la fraction de puissance arrivant à l’antenne qui va être
captée puis transformée en puissance de sortie dépend de la direction (
a), qui
vont toutes contribuer plus ou moins à la TA. Le deuxième processus à considérer est que
l’antenne est directive, c’est à dire que la fraction de puissance arrivant à l’antenne qui va être
captée puis transformée en puissance de sortie dépend de la direction ( a,
a, a) d’où provient le
rayonnement.
a) d’où provient le
rayonnement.
Seule une fraction de l’énergie arrivant dans la direction ( a,
a, a) est captée par l’antenne à cause des
interférences destructives liées à la forme du capteur. De plus, de l’énergie va se dissiper dans le milieu à
pertes que constitue l’antenne. La répartition angulaire de la puissance captée (Pc) par l’antenne (i.e.
sans prendre en compte les pertes) définit le diagramme d’antenne normalisé Fn(
a) est captée par l’antenne à cause des
interférences destructives liées à la forme du capteur. De plus, de l’énergie va se dissiper dans le milieu à
pertes que constitue l’antenne. La répartition angulaire de la puissance captée (Pc) par l’antenne (i.e.
sans prendre en compte les pertes) définit le diagramme d’antenne normalisé Fn( a,
a, a). Il s’agit de la
puissance captée Pc(
a). Il s’agit de la
puissance captée Pc( a,
a, a) normalisée à la Pc maximale parmi toutes les directions. On en déduit la
directivité (D), qui traduit la Pc(
a) normalisée à la Pc maximale parmi toutes les directions. On en déduit la
directivité (D), qui traduit la Pc( a,
a, a) normalisée à la Pc moyenne sur toutes les directions.
Ainsi,
a) normalisée à la Pc moyenne sur toutes les directions.
Ainsi,
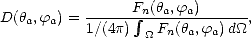
où d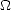 = sin
= sin  d
d d
d est l’angle solide élémentaire. Pour une antenne idéale sans pertes, on a
alors
est l’angle solide élémentaire. Pour une antenne idéale sans pertes, on a
alors
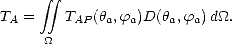 | (2.17) |
Ainsi, la TA résulte de la somme des TAP pondérées par la directivité de l’antenne dans toutes les directions. En réalité, une antenne présente toujours des pertes par dissipation thermique et l’on définit le gain de l’antenne G comme
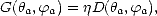 | (2.18) |
où 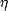 a est l’efficacité de l’antenne définie comme le rapport entre la puissance captée et la puissance en
sortie de l’antenne.
a est l’efficacité de l’antenne définie comme le rapport entre la puissance captée et la puissance en
sortie de l’antenne.