
 ) de l’eau de mer caractérise
ses propriétés diélectriques et dépend, à une fréquence donnée, de la salinité et de la température de l’eau.
C’est en mesurant les propriétés diéléctriques de l’océan que l’on va retrouver la salinité. Pour mesurer à
distance ces propriétés diélectriques, on va mesurer l’énergie rayonnée (i.e. l’énergie électromagnétique
(EM) émise) par la mer.
) de l’eau de mer caractérise
ses propriétés diélectriques et dépend, à une fréquence donnée, de la salinité et de la température de l’eau.
C’est en mesurant les propriétés diéléctriques de l’océan que l’on va retrouver la salinité. Pour mesurer à
distance ces propriétés diélectriques, on va mesurer l’énergie rayonnée (i.e. l’énergie électromagnétique
(EM) émise) par la mer.
En faisant l’hypothèse que l’océan est à l’équilibre thermodynamique, il s’établit un équilibre entre les processus radiatifs d’absorption et d’émission à une température donnée. Comme l’énergie absorbée par l’eau de mer dépend de sa permittivité, on peut estimer cette dernière à partir de l’énergie rayonnée par l’océan, et ainsi estimer la salinité.
La propagation d’une onde EM dans un milieu à pertes (i.e. dont la conductivité  n’est pas nulle)
dépend de la permittivité complexe
n’est pas nulle)
dépend de la permittivité complexe  c (ou constante diélectrique) du milieu
c (ou constante diélectrique) du milieu
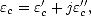 | (2.1) |
où  c ' et
c ' et  c '' sont respectivement les parties réelles et imaginaires de
c '' sont respectivement les parties réelles et imaginaires de  c. Les champs électrique et
magnétiques d’une onde EM satisfaisant les équations de Maxwell (voir l’annexe A) s’écrivent
c. Les champs électrique et
magnétiques d’une onde EM satisfaisant les équations de Maxwell (voir l’annexe A) s’écrivent
![E(r) = E(0).exp[j(wt ± k.r)] (2.2)
H(r) = H(0).exp[j(wt ± k.r)] (2.3)](plan_html18x.gif)
où 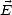 (0) et
(0) et 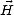 (0) sont des vecteurs constants,
(0) sont des vecteurs constants,  est la pulsation de l’onde EM, t est le
temps,
est la pulsation de l’onde EM, t est le
temps, 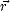 est le vecteur de déplacement et
est le vecteur de déplacement et 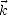 est le vecteur d’onde dont la norme k est définie
par
est le vecteur d’onde dont la norme k est définie
par
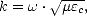 | (2.4) |
où 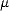 est la perméabilité magnétique du milieu. On définit la permittivité relative
est la perméabilité magnétique du milieu. On définit la permittivité relative  r du milieu
comme
r du milieu
comme
où  0 est la permittivité du vide, et l’on suppose que la perméabilité de l’eau de mer est celle du vide,
c’est à dire que la perméabilité relative
0 est la permittivité du vide, et l’on suppose que la perméabilité de l’eau de mer est celle du vide,
c’est à dire que la perméabilité relative 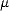 r vaut 1 (voir l’annexe C). On en déduit l’indice de réfraction
(voir l’annexe D) complexe
r vaut 1 (voir l’annexe C). On en déduit l’indice de réfraction
(voir l’annexe D) complexe
où n' est la partie réelle de l’indice de réfraction, qui va déterminer le déphasage de l’onde lors de la propagation dans le milieu et n'' est sa partie imaginaire, qui va déterminer l’atténuation de l’onde (voir l’annexe E). On déduit de (2.7) et (2.8) et de l’annexe F que
On voit ainsi, d’après (2.10), que les parties réelles et imaginaires de  r vont contribuer à l’atténuation
de l’onde EM par le milieu. Dans le cas qui nous intéresse, le milieu à perte est l’eau de mer dont
l’absorptivité va dépendre de sa permittivité. En utilisant le modèle de permittivité de [47] (voir section
4.2) à la fréquence de 1.4 GHz (voir la section 2.2), à SST = 18oC et SSS = 35psu, on détermine
r vont contribuer à l’atténuation
de l’onde EM par le milieu. Dans le cas qui nous intéresse, le milieu à perte est l’eau de mer dont
l’absorptivité va dépendre de sa permittivité. En utilisant le modèle de permittivité de [47] (voir section
4.2) à la fréquence de 1.4 GHz (voir la section 2.2), à SST = 18oC et SSS = 35psu, on détermine
 c = 72.6 - j64.6 et une épaisseur de peau
c = 72.6 - j64.6 et une épaisseur de peau 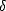 = 9.3 mm (
= 9.3 mm (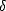 est de l’ordre du centimètre pour les
températures et salinités rencontrées à la surface de l’océan, il peut atteindre la dizaine de centimètres
pour l’eau douce).
est de l’ordre du centimètre pour les
températures et salinités rencontrées à la surface de l’océan, il peut atteindre la dizaine de centimètres
pour l’eau douce).