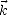 est le long d’un vecteur unitaire
est le long d’un vecteur unitaire 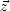 quelconque (i.e.
quelconque (i.e. 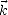 = k
= k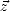 ), la phase est donnée par
), la phase est donnée par
Pour un champ électrique satisfaisant (A.8) et dont le vecteur d’onde 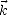 est le long d’un vecteur unitaire
est le long d’un vecteur unitaire 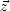 quelconque (i.e.
quelconque (i.e. 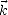 = k
= k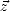 ), la phase est donnée par
), la phase est donnée par
En imposant que la phase  soit constante, on trouve qu’à un instant donné t, tous les points
appartenant au plan orthogonal au vecteur d’onde
soit constante, on trouve qu’à un instant donné t, tous les points
appartenant au plan orthogonal au vecteur d’onde 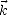 (i.e. en z=constante) ont la même phase. C’est ce qui
caractérise une onde plane. On remarque que la phase se propage au cours du temps le long de
(i.e. en z=constante) ont la même phase. C’est ce qui
caractérise une onde plane. On remarque que la phase se propage au cours du temps le long de 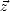 ,
donc que l’onde se propage le long de
,
donc que l’onde se propage le long de 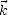 . S’il on suppose que l’onde se propage selon les z
croissants2 ,
on a
. S’il on suppose que l’onde se propage selon les z
croissants2 ,
on a
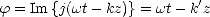 | (E.35) |
où k' est la partie réelle du nombre d’onde. On alors définit la vitesse de phase comme la vitesse vp de propagation du plan de phase constante et on a
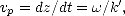 | (E.36) |
soit, d’après (A.10) et (D.32),
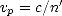 | (E.37) |
où n' est la partie réelle de n. D’après (A.8), l’atténuation du champ électrique est exponentielle et
dépend du coefficient 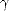 = Re
= Re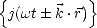 . Si, comme précédemment, le vecteur d’onde est le long de
. Si, comme précédemment, le vecteur d’onde est le long de 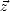 ,
on a
,
on a
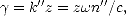 | (E.38) |
où k'' est la partie imaginaire de k et n'' la partie imaginaire de n. L’atténuation de l’onde augmente
avec la distance z. On en déduit l’épaisseur de peau 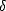 = c/(
= c/( n''), définie comme la distance pour laquelle
l’onde est atténuée d’un facteur 1/e.
n''), définie comme la distance pour laquelle
l’onde est atténuée d’un facteur 1/e.