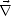 ×à (A.2) et l’on
obtient
×à (A.2) et l’on
obtient
Pour déterminer l’expression du champ électrique, on applique l’opérateur 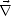 ×à (A.2) et l’on
obtient
×à (A.2) et l’on
obtient
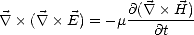 | (A.5) |
En utilisant la propriété
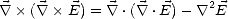 | (A.6) |
où 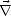 . est l’opérateur divergence ou gradient selon qu’il est appliqué respectivement à un champ
vectoriel ou scalaire et en supposant que le milieu est homogène et vide de charges libres, de sorte que
(A.4) est vérifiée on obtient l’équation homogène en champ électrique
. est l’opérateur divergence ou gradient selon qu’il est appliqué respectivement à un champ
vectoriel ou scalaire et en supposant que le milieu est homogène et vide de charges libres, de sorte que
(A.4) est vérifiée on obtient l’équation homogène en champ électrique
![[ ]
2 @2E @E
\~/ E = m e@t2-+ s-@t .](plan_html733x.gif) | (A.7) |
On a alors comme solution satisfaisant l’équation homogène (A.7), l’expression complexe du champ électrique
![E(r,t) = E(0).exp[j(wt ± k.r)]](plan_html734x.gif) | (A.8) |
où 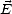 (0) est un vecteur constant,
(0) est un vecteur constant,  est la pulsation du champ électrique, t est le temps et
est la pulsation du champ électrique, t est le temps et 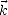 est le
vecteur d’onde dont la norme k (i.e. le nombre d’onde) est définie par
est le
vecteur d’onde dont la norme k (i.e. le nombre d’onde) est définie par
où l’on a défini la constante diélectrique du milieu par
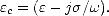 | (A.11) |
On notera que la permittivité  c, et par conséquent le nombre d’onde, d’un milieu à pertes par conduction
est complexe à cause du terme en j
c, et par conséquent le nombre d’onde, d’un milieu à pertes par conduction
est complexe à cause du terme en j /
/ . On vera dans la section G que
. On vera dans la section G que  peut aussi être
complexe, traduisant des pertes liée au mécanismes de polarisation du milieu. On parle alors de
constante diélectrique. On peut déduire de même des equations de Maxwell (A.1) et (A.2)
que
peut aussi être
complexe, traduisant des pertes liée au mécanismes de polarisation du milieu. On parle alors de
constante diélectrique. On peut déduire de même des equations de Maxwell (A.1) et (A.2)
que
![H(r, t) = H(0).exp[j(wt± k.r)].](plan_html739x.gif) | (A.12) |
On dérive les champs électrique et magnétique réels des solutions complexes (A.8) et (A.12) à partir des relations