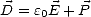
Dans un diélectrique, on écrit l’induction électrique
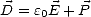 | (G.40) |
où 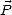 est le vecteur polarisation qui traduit l’influence du champ électrique sur les constituants du
milieu. Ce phénomène est lié au déplacement des charges positives et négatives et permet au milieu
d’emmagasiner de l’énergie, fournie par le champ électrique. Il existe plusieurs types de polarisations
possibles dans un milieu, comme les polarisations par charge d’espace (accumulations de charges),
dipolaire (orientation des molécules polaires avec le champ électrique), ionique (séparation des ions
positifs et négatifs de la molécule) ou électronique (déplacement du nuage électronique par rapport au
noyau). La polarisabilité par charge d’espace varie avec la fréquence dans le domaine des basses
fréquences, les polarisabilité ionique et électronique variant respectivement dans les infrarouges et les
ultraviolets. C’est la polarisabilité dipolaire, ou polarisation d’orientation, qui varie dans le domaine des
ondes hyperfréquences et que je vais décrire dans ce qui suit.
est le vecteur polarisation qui traduit l’influence du champ électrique sur les constituants du
milieu. Ce phénomène est lié au déplacement des charges positives et négatives et permet au milieu
d’emmagasiner de l’énergie, fournie par le champ électrique. Il existe plusieurs types de polarisations
possibles dans un milieu, comme les polarisations par charge d’espace (accumulations de charges),
dipolaire (orientation des molécules polaires avec le champ électrique), ionique (séparation des ions
positifs et négatifs de la molécule) ou électronique (déplacement du nuage électronique par rapport au
noyau). La polarisabilité par charge d’espace varie avec la fréquence dans le domaine des basses
fréquences, les polarisabilité ionique et électronique variant respectivement dans les infrarouges et les
ultraviolets. C’est la polarisabilité dipolaire, ou polarisation d’orientation, qui varie dans le domaine des
ondes hyperfréquences et que je vais décrire dans ce qui suit.
Une molécule asymmétrique, comme par exemple la molécule d’eau, va présenter un dipôle permanent même en l’absence de champ extérieur. On parle alors de molécule polaire. Sans champ électrique extérieur, les molécules sont organisées de sorte que le moment dipolaire global soit nul. Lors de l’application d’un champ électrique extérieur, les dipôles vont s’orienter le long du champ.
Lors de l’application d’un champ électrique variable, soit le mécanisme de polarisation arrive à suivre
les variations du champ et alors les dipôles sont en phase avec le champ, soit il existe un déphasage entre
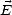 et
et 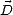 . Lorsque les dipôles sont en phase avec le champ électrique, c’est à dire que
. Lorsque les dipôles sont en phase avec le champ électrique, c’est à dire que 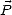 ||
||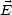 , on
a
, on
a
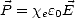 | (G.41) |
soit
où 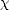 e est la susceptibilité électrique du milieu et
e est la susceptibilité électrique du milieu et  est la permittivité du milieu qui est une grandeur
réelle. Dans le domaine des hyperfréquences, les mécanismes de polarisation qui seront en phase avec le
champ électrique sont les polarisations ionique et électronique pour lesquels le régime est similaire au
régime statique. Par contre, l’orientation des molécules polaires (i.e. la polarisation dipolaire) va subir un
temps de relaxation par rapport à
est la permittivité du milieu qui est une grandeur
réelle. Dans le domaine des hyperfréquences, les mécanismes de polarisation qui seront en phase avec le
champ électrique sont les polarisations ionique et électronique pour lesquels le régime est similaire au
régime statique. Par contre, l’orientation des molécules polaires (i.e. la polarisation dipolaire) va subir un
temps de relaxation par rapport à 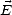 à cause des forces engendrées par les interactions entre les molécules
qui s’opposent à la rotation. Dans ce cas,
à cause des forces engendrées par les interactions entre les molécules
qui s’opposent à la rotation. Dans ce cas,  dans l’expression (G.44) n’est plus réel et sa partie
imaginaire traduit le déphasage entre
dans l’expression (G.44) n’est plus réel et sa partie
imaginaire traduit le déphasage entre 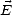 et
et 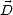 . On exprime alors l’induction électrique sous la
forme
. On exprime alors l’induction électrique sous la
forme
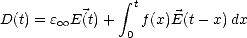 | (G.45) |
où 
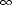 est une constante réelle qui résulte des mécanismes de polarisation en phase avec
est une constante réelle qui résulte des mécanismes de polarisation en phase avec 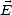 , et
f(x)
, et
f(x)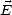 (t - x) est la contribution du champ
(t - x) est la contribution du champ 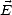 à l’instant t - x.
à l’instant t - x.
Si le champ 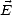 est de la forme (A.8), (G.45) devient
est de la forme (A.8), (G.45) devient
![integral t
D(t) = e oo E(t) + E(0).exp [j(wtħ k.r)] f(x)exp[- jwx]dx (G.46)
0
= e(w)E(t) (G.47)](plan_html822x.gif)
et on a
![integral t
e(w) = e oo + f(x)exp [- jwx]dx.
0](plan_html823x.gif) | (G.48) |
Si l’on suppose que t est grand et que la fonction f(x) tend vers 0 à t = 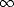 , alors l’intégrale est la
tranformée de Fourier de f(x). Si l’on suppose que la décroissance de l’influence du champ électrique est
une loi exponentielle avec un temps de relaxation
, alors l’intégrale est la
tranformée de Fourier de f(x). Si l’on suppose que la décroissance de l’influence du champ électrique est
une loi exponentielle avec un temps de relaxation  r, de sorte que f(x) = f0 exp[ -t/
r, de sorte que f(x) = f0 exp[ -t/ ], et que l’on pose
comme limite basse et haute fréquence
], et que l’on pose
comme limite basse et haute fréquence

alors on obtient la loi de Debye [18] suivante
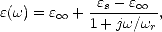 | (G.51) |
où  r = 1/
r = 1/ .
.