![[ ( ) ( )]
f(t) = a0+ S oo a cos 2pn t- + b sin 2pn t- ,
2 n=1 n P n P](plan_html826x.gif)
Toute fonction réelle périodique f(t) de période P peut se décomposer sous la forme:
![[ ( ) ( )]
f(t) = a0+ S oo a cos 2pn t- + b sin 2pn t- ,
2 n=1 n P n P](plan_html826x.gif) | (H.52) |
où a0 , an et bn sont des réels, les coefficients de Fourier. Ils sont donnés par
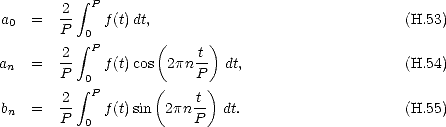
On peut remarquer que le premier terme de la série, a0/2, représente la valeur moyenne de
f(t) sur une période. Pour le cas du spectre de mer, on pose t =  0, P = 2
0, P = 2 et on dérive de
(H.52)
et on dérive de
(H.52)
![Y(k, f0) = Y0(k,f0)+ S oo n=1 [Yn(k,f0) cos(nf0) +Y*nsin(nf0)],](plan_html828x.gif) | (H.56) |
où
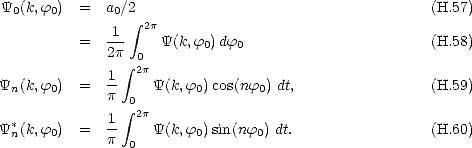
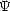 (k,
(k,  0 ) étant symmétrique par rapport à la direction du vent, donc en
0 ) étant symmétrique par rapport à la direction du vent, donc en  0, elle est décomposé
uniquement sur une base de fonctions paires, c’est à dire sur les cos
0, elle est décomposé
uniquement sur une base de fonctions paires, c’est à dire sur les cos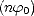 . On en déduit
. On en déduit 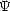 n*(k,
n*(k, 0) = 0
quelque soit n.
0) = 0
quelque soit n.