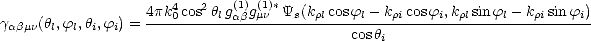
Les coefficients de diffusion bistatique d’ordre un, utilisés dans (4.108), sont donnés par ([105]) en nombre d’onde ou par ([102]) comme suit:
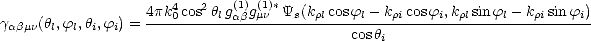 | (I.61) |
où
![[ V~ ------2-- V~ ------2--- ]
g(1)(h,f,h,f ) = 2-coshi(er(--1)-ersin-hlsinhi---e)r(--sin--hl-er--sin--hicos()fl--fi)-,
vvllii er cos hl + V~ er- sin2hl ercoshi + V~ er - sin2hi](plan_html832x.gif) | (I.62) |
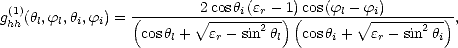 | (I.63) |
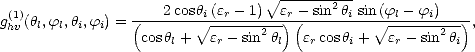 | (I.64) |
et
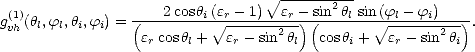 | (I.65) |
 s est le spectre de puissance des petites échelles de vague (voir section 4.3.1), k
s est le spectre de puissance des petites échelles de vague (voir section 4.3.1), k l = k0 sin
l = k0 sin l et
k
l et
k i = k0 sin
i = k0 sin  i .
i .
Les coefficients de diffusion bistatique d’ordre deux, utilisés dans (4.104), sont donnés par ([105]) en nombre d’onde ou par ([102]) comme suit:
et
avec  = k
= k '/k0.
'/k0.