|
|
La structure de la surface de la mer peut être considérée comme le résultat d’un processus aléatoire dans le sens où il n’est pas possible de prédire une partie du profil de la surface à partir de la connaissance du profil d’une autre partie de cette surface (de même qu’il n’est pas possible de prédire le profil de cette surface à un instant donné à partir de la connaissance du profil à un instant antérieur). On va donc décrire cette surface par ses propriétés statistiques.
|

|
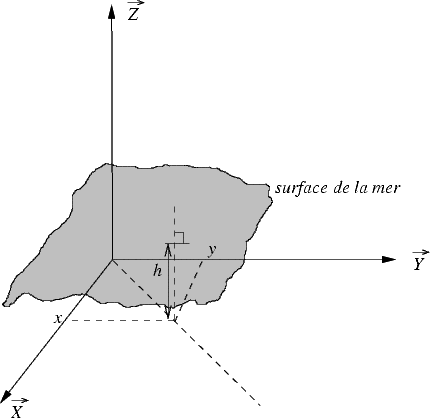
La première caractéristique que l’on va définir est la hauteur h(x,y,t) de la surface de la mer par
rapport à une surface de référence, où h est une variable aléatoire à trois dimensions (3D) (voir la figure
4.6). Je vais séparer les variations spatiales des variations temporelles, en sachant qu’elles sont reliées
par la physique du milieu et par l’équation de dispersion donnée en (4.32). Les variations
spatiales de la hauteur sont définies par une variable aléatoire à deux dimensions (2D) h(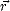 ),
où
),
où 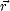 = x
= x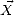 + y
+ y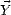 . On associe à h une distribution statistique p(h), où p(h)dh détermine la
probabilité de n’importe quel point situé en
. On associe à h une distribution statistique p(h), où p(h)dh détermine la
probabilité de n’importe quel point situé en 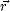 d’être à une hauteur comprise entre h et h + dh par
rapport à la surface de référence. La surface moyenne (spatialement) de la mer est choisie
comme surface de référence, de sorte que le moment d’ordre un (i.e. la moyenne) de h soit
nul:
d’être à une hauteur comprise entre h et h + dh par
rapport à la surface de référence. La surface moyenne (spatialement) de la mer est choisie
comme surface de référence, de sorte que le moment d’ordre un (i.e. la moyenne) de h soit
nul:
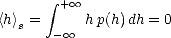 | (4.16) |
où l’opérateur 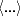 s désigne une moyenne spatiale. Ainsi, la somme de la profondeur des creux et de la
hauteur des bosses se compense.
s désigne une moyenne spatiale. Ainsi, la somme de la profondeur des creux et de la
hauteur des bosses se compense.
On a alors
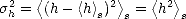 | (4.17) |
où  h est l’écart type des hauteurs, et
h est l’écart type des hauteurs, et  h2 est la variance des hauteurs, qui est égale ici à la puissance
du signal h(
h2 est la variance des hauteurs, qui est égale ici à la puissance
du signal h(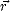 ). L’écart type des hauteurs
). L’écart type des hauteurs  h est la moyenne quadratique de l’écart entre la surface de la
mer et la surface de référence. À l’aide des paramètres précédemments définis (la distribution des
hauteurs p(h) et la variance des hauteurs
h est la moyenne quadratique de l’écart entre la surface de la
mer et la surface de référence. À l’aide des paramètres précédemments définis (la distribution des
hauteurs p(h) et la variance des hauteurs  h2), on ne définit pas complètemment la statistique du profil
de la surface car on se limite à la dimension verticale. Or une variation de hauteur h donnée peut se faire
sur une échelle de longueur (i.e. une distance horizontale
h2), on ne définit pas complètemment la statistique du profil
de la surface car on se limite à la dimension verticale. Or une variation de hauteur h donnée peut se faire
sur une échelle de longueur (i.e. une distance horizontale 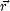 ) plus ou moins grande. Pour plusieurs surfaces
ayant les mêmes p(h) et
) plus ou moins grande. Pour plusieurs surfaces
ayant les mêmes p(h) et  h, on peut obtenir des profils très différents à cause d’échelles de
longueurs différentes ([67]). Pour discerner ces différents profils, il faut prendre en compte la
corrélation horizontale 2D de h(
h, on peut obtenir des profils très différents à cause d’échelles de
longueurs différentes ([67]). Pour discerner ces différents profils, il faut prendre en compte la
corrélation horizontale 2D de h(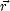 ) sur une distance
) sur une distance 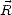 , définie par la fonction d’autocorrélation
2D
, définie par la fonction d’autocorrélation
2D
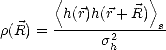 | (4.18) |
ou encore par la fonction d’autocovariance 2D définie comme 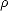 0(
0(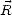 ) =
) =  h2
h2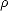 (
(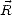 ), qui est égale à la
fonction d’autocorrélation non normalisée et dont l’unité est le m2. À partir de la fonction
d’autocovariance 2D, on définit le spectre de puissance 2D (en m4) de la surface océanique
comme
), qui est égale à la
fonction d’autocorrélation non normalisée et dont l’unité est le m2. À partir de la fonction
d’autocovariance 2D, on définit le spectre de puissance 2D (en m4) de la surface océanique
comme
![[ ]
Y(k) = TF r0(R)](plan_html162x.gif) | (4.19) |
où TF est la transformée de Fourier, et 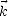 = kx
= kx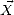 + ky
+ ky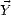 est le vecteur d’onde en rad.m-1. Le spectre
de puissance
est le vecteur d’onde en rad.m-1. Le spectre
de puissance 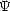 contient les informations à la fois sur la hauteur de la surface et sur le taux de variation
des hauteurs avec
contient les informations à la fois sur la hauteur de la surface et sur le taux de variation
des hauteurs avec 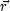 (c’est à dire sur les pentes de la surface).
(c’est à dire sur les pentes de la surface).