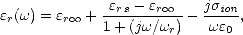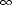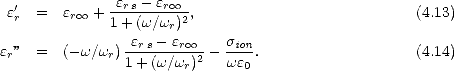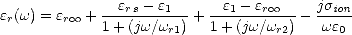Les modèles existants de constante diélectrique relative pour l’eau de mer reposent sur une
approche semi-empirique:  r est relié à la fréquence électromagnétique
r est relié à la fréquence électromagnétique  par une fonction
paramétrique dont les paramètres sont ajustés sur des mesures de constante diélectrique à différentes
températures et salinités (i.e. les paramètres dépendent de la température et de la salinité). La
fonction paramétrique est l’équation de relaxation, proposée par Debye ([18] pour les molécules
polaires, voir l’annexe G) à partir d’hypothèse physiques. On déduit de (2.5), (A.11) et (G.51),
l’équation à un temps de relaxation pour la constante diélectrique relative de l’eau de mer
suivante:
par une fonction
paramétrique dont les paramètres sont ajustés sur des mesures de constante diélectrique à différentes
températures et salinités (i.e. les paramètres dépendent de la température et de la salinité). La
fonction paramétrique est l’équation de relaxation, proposée par Debye ([18] pour les molécules
polaires, voir l’annexe G) à partir d’hypothèse physiques. On déduit de (2.5), (A.11) et (G.51),
l’équation à un temps de relaxation pour la constante diélectrique relative de l’eau de mer
suivante:
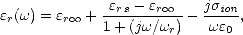 | (4.12) |
où  r s =
r s =  s /
s / 0 est la permittivité statique relative (i.e.
0 est la permittivité statique relative (i.e.  r pour
r pour 
 0),
0),  r
r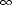 =
= 
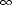 /
/ 0 est la
permittivité relative à haute fréquence,
0 est la
permittivité relative à haute fréquence,  = 2
= 2
 est la pulsation de l’onde,
est la pulsation de l’onde,  r est la pulsation de
relaxation,
r est la pulsation de
relaxation,  ion est la conductivité ionique de l’eau de mer (Sm-1) et
ion est la conductivité ionique de l’eau de mer (Sm-1) et  0 est la permittivité du vide.
La permittivité relative est composée d’une partie réelle (
0 est la permittivité du vide.
La permittivité relative est composée d’une partie réelle ( r') et imaginaire (
r') et imaginaire ( r”) données
par
r”) données
par
Le premier terme de  r” dans (4.14) traduit l’atténuation de l’onde par le phénomène de
polarisation dipolaire (voir l’annexe G), alors que le deuxième terme traduit les pertes par
conduction. On verra par la suite qu’en bande L, le terme de pertes par conduction l’emporte sur
celui dû à la polarisation dipolaire. Les paramètres
r” dans (4.14) traduit l’atténuation de l’onde par le phénomène de
polarisation dipolaire (voir l’annexe G), alors que le deuxième terme traduit les pertes par
conduction. On verra par la suite qu’en bande L, le terme de pertes par conduction l’emporte sur
celui dû à la polarisation dipolaire. Les paramètres  rs,
rs,  r
r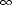 ,
,  r, et
r, et  ion dépendent de la
température et de la salinité. Il est supposé dans tous les modèles que
ion dépendent de la
température et de la salinité. Il est supposé dans tous les modèles que  ion est indépendant de la
fréquence, ainsi que de la pression puisque l’on s’intéresse à la conductivité de l’eau de mer de
surface.
ion est indépendant de la
fréquence, ainsi que de la pression puisque l’on s’intéresse à la conductivité de l’eau de mer de
surface.
Il existe très peu de mesures de la permittivité de l’eau de mer naturelle, particulièrement à 1.4
GHz ou aux basses radiofréquences en général. Comme la permittivité d’un solution NaCl
diffère notablement de celle de l’eau de mer [32], je ne traiterai que des modèles basés sur
des mesures effectuées avec, au moins en partie, des échantillons d’eau de mer naturelle. Les
premières mesures ont été effectuées dans les années 70 par Ho et Hall ([37]) et Ho et al.
([38 ]) respectivement aux fréquence de 2.653 GHz et 1.43 GHz, sur des échantillons d’eau
de mer et de solution NaCl. La précision annoncée sur les mesures en bande L est de 0.2%
et 0.4% respectivement sur les parties réelles et imaginaires de  r. Cependant, [47], qui ont
basé leur modèle de
r. Cependant, [47], qui ont
basé leur modèle de  r sur ces mesures (cité comme le modèle KS par la suite), ont mis en
évidence l’existence d’un biais sur
r sur ces mesures (cité comme le modèle KS par la suite), ont mis en
évidence l’existence d’un biais sur  r' mesuré par Ho et al.. La précision annoncée paraît donc
optimiste. De plus, peu de mesures ont été effectuées dans l’intervalle de salinité 30-40 psu, qui
concerne l’essentiel de la surface des océans, la plupart ayant été effectuée entre 4 et 30 psu.
Plus récemment, [32] ont proposé un modèle (modèle EL) basé sur des mesures faites à des
fréquences comprises entre 3 et 20 GHz, ainsi qu’aux fréquences 23.8, 36.5 et 89 GHz avec
une précision absolue annoncée de 1%. Cependant, [85] a déterminé que la simplicité des
régressions utilisées pour
r' mesuré par Ho et al.. La précision annoncée paraît donc
optimiste. De plus, peu de mesures ont été effectuées dans l’intervalle de salinité 30-40 psu, qui
concerne l’essentiel de la surface des océans, la plupart ayant été effectuée entre 4 et 30 psu.
Plus récemment, [32] ont proposé un modèle (modèle EL) basé sur des mesures faites à des
fréquences comprises entre 3 et 20 GHz, ainsi qu’aux fréquences 23.8, 36.5 et 89 GHz avec
une précision absolue annoncée de 1%. Cependant, [85] a déterminé que la simplicité des
régressions utilisées pour  ion dans le modèle EL était inadaptée pour déterminer
ion dans le modèle EL était inadaptée pour déterminer  r aux basses
fréquences et entrainaît des écarts sensibles entre
r aux basses
fréquences et entrainaît des écarts sensibles entre  ion prédits et mesurés. Il a évalué cet écart à
8% pour une salinité de 20 psu et une température de -2oC, ce qui est très supérieur à la
précision de 1% annoncée sur la mesure de conductivité. [86] ont proposé un modèle (modèle
ST95) basé sur des mesures faites à des fréquences comprises entre 7 GHz et 14 GHz, et [85] a
proposé un modèle (modèle ST97) reposant sur les mesures de [86] et de [32]. Le modèle ST97
conserve la paramétrisation de
ion prédits et mesurés. Il a évalué cet écart à
8% pour une salinité de 20 psu et une température de -2oC, ce qui est très supérieur à la
précision de 1% annoncée sur la mesure de conductivité. [86] ont proposé un modèle (modèle
ST95) basé sur des mesures faites à des fréquences comprises entre 7 GHz et 14 GHz, et [85] a
proposé un modèle (modèle ST97) reposant sur les mesures de [86] et de [32]. Le modèle ST97
conserve la paramétrisation de  ion déterminée pour le modèle ST95, de même que les équations
déterminant les paramètres de la loi de Debye pour de l’eau douce. Il est à noter que les
modèles ST95 et ST97 reposent sur une équation de Debye à deux pulsations de relaxation de la
forme
ion déterminée pour le modèle ST95, de même que les équations
déterminant les paramètres de la loi de Debye pour de l’eau douce. Il est à noter que les
modèles ST95 et ST97 reposent sur une équation de Debye à deux pulsations de relaxation de la
forme
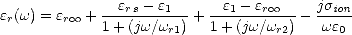 | (4.15) |
où  1 est une permittivité intermédiaire, et
1 est une permittivité intermédiaire, et  r1 et
r1 et  r2 sont les deux pulsations de relaxation. Une telle
équation à deux pulsations de relaxation s’avère nécessaire pour des études sur des larges gammes de
fréquence. Cependant, comme
r2 sont les deux pulsations de relaxation. Une telle
équation à deux pulsations de relaxation s’avère nécessaire pour des études sur des larges gammes de
fréquence. Cependant, comme  r2 = 1000 rad.s-1 dans les modèles ST95 et ST97, ce qui
correspond à une fréquence de 160 GHz environ, on peut se ramener aux basses fréquences à une
relation de la forme de (4.12). Enfin, très récemment [4] ont proposé un nouveau modèle
développé spécifiquement pour la bande L. Je n’en traiterai que succintement dans la partie
5.1, pour ce qui concerne la Tb prédite avec ce modèle, car aucune référence n’est encore
disponible. D’autre part, des mesures sont en cours à l’université de Washington, toujours en bande
L.
r2 = 1000 rad.s-1 dans les modèles ST95 et ST97, ce qui
correspond à une fréquence de 160 GHz environ, on peut se ramener aux basses fréquences à une
relation de la forme de (4.12). Enfin, très récemment [4] ont proposé un nouveau modèle
développé spécifiquement pour la bande L. Je n’en traiterai que succintement dans la partie
5.1, pour ce qui concerne la Tb prédite avec ce modèle, car aucune référence n’est encore
disponible. D’autre part, des mesures sont en cours à l’université de Washington, toujours en bande
L.
Il est difficile de déterminer a priori quel est le modèle susceptible d’être le plus fiable en bande L. Le
modèle KS repose sur les seules mesures (jusqu’à très récemment) effectuées en bande L, mais
celles-ci sont en faible nombre et peu fiables (à cause de la précision mise en défaut par [47] et
de l’utilisation de solution de NaCl). Les modèles EL, ST95 et ST97 ont été développés à
plus haute fréquence que 1.4 GHz et, bien que (4.12) nous permette de déterminer  r en
bande L, il est probable que la précision annoncée pour ces modèles sera dégradée en bande
L. De plus, le modèle EL a été développé pour des salinités supérieures à 20 psu (ce qui se
traduit par exemple par le fait que
r en
bande L, il est probable que la précision annoncée pour ces modèles sera dégradée en bande
L. De plus, le modèle EL a été développé pour des salinités supérieures à 20 psu (ce qui se
traduit par exemple par le fait que  ion prédite par ce modèle pour de l’eau douce n’est pas
nulle) et l’imprécision sur
ion prédite par ce modèle pour de l’eau douce n’est pas
nulle) et l’imprécision sur  ion ([85]) est critique pour l’estimation de la SSS. C’est pour ces
raisons que j’ai évalué les différences entre les différents modèles en terme de
ion ([85]) est critique pour l’estimation de la SSS. C’est pour ces
raisons que j’ai évalué les différences entre les différents modèles en terme de  r et surtout
l’incertitude induite par ces différences sur la Tbmer (ce sujet sera discuté dans la section
5.1).
r et surtout
l’incertitude induite par ces différences sur la Tbmer (ce sujet sera discuté dans la section
5.1).
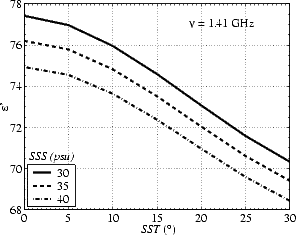
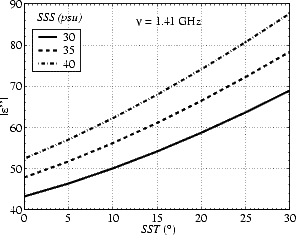
La constante diélectrique à 1.41 GHz, calculée à partir du modèle KS, est reportée sur les figures 4.4.a
(partie réelle) et 4.4.b (valeur absolue de la partie imaginaire) pour différentes SST et SSS. On constate
que  r '' est beaucoup plus sensible à la SST et à la SSS que
r '' est beaucoup plus sensible à la SST et à la SSS que  r'. En effet, quand la SSS varie de 30 à
40 psu,
r'. En effet, quand la SSS varie de 30 à
40 psu,  r '' varie de +23% et
r '' varie de +23% et  r' de -3%. De même, quand la SST varie de 0 à 30oC,
r' de -3%. De même, quand la SST varie de 0 à 30oC,  r''
varie de +60% et
r''
varie de +60% et  r' de -10%. La différence entres les constantes diélectriques prédites par
les différents modèles est reportée et discutée dans la section 2 de l’article en annexe P. La
différence est la plus grande entre les modèles KS et EL ; le modèle KS prédit des
r' de -10%. La différence entres les constantes diélectriques prédites par
les différents modèles est reportée et discutée dans la section 2 de l’article en annexe P. La
différence est la plus grande entre les modèles KS et EL ; le modèle KS prédit des  r' et
r' et  r''
systématiquement plus grands de 0% à environ 4.5% selon la SST que ceux prédits par le modèle
EL. Cette différence entre les modèles varie plus faiblement avec la SSS, indiquant un relatif
accord des modèles sur l’influence de la salinité. Les modèles ST97 et ST95 prédisent des
résultats peu différents entre eux, et compris entre les prédictions du modèle KS et du modèle
EL.
r''
systématiquement plus grands de 0% à environ 4.5% selon la SST que ceux prédits par le modèle
EL. Cette différence entre les modèles varie plus faiblement avec la SSS, indiquant un relatif
accord des modèles sur l’influence de la salinité. Les modèles ST97 et ST95 prédisent des
résultats peu différents entre eux, et compris entre les prédictions du modèle KS et du modèle
EL.
Dans le modèle simple exposé dans la section 2.3, la Tb de la mer (Tbmer) est directement relié aux
coefficients de réflexion de Fresnel, donnés par (2.23). Bien que ce modèle soit insuffisant pour décrire tous
les processus impliqués dans l’émissivité de la surface de la mer, on verra dans la section 5.1 que
l’essentiel du signal en salinité et en température est dû aux coefficients donnés en (2.23), et
donc que ce modèle rend compte relativement bien de la variation de Tbmer avec la SSS et la
SST.
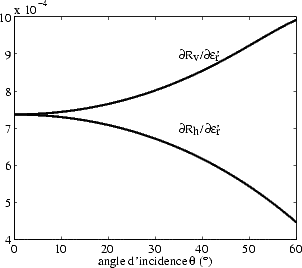
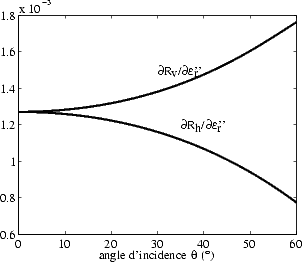
La sensibilité des coefficients de Fresnel aux parties réelles et imaginaires de  r est reportée sur la
figure 4.5. Les coefficients de reflexion sont plus sensibles à
r est reportée sur la
figure 4.5. Les coefficients de reflexion sont plus sensibles à  r'' qu’à
r'' qu’à  r'. On a vu par ailleurs que
r'. On a vu par ailleurs que  r'' est
beaucoup plus sensible à la SST et à la SSS que
r'' est
beaucoup plus sensible à la SST et à la SSS que  r'. D’autre part, le terme j
r'. D’autre part, le terme j ion/(
ion/(
 0) représente de 75%
(pour les faibles SST) à 95% (pour les fortes SST) de la valeur de
0) représente de 75%
(pour les faibles SST) à 95% (pour les fortes SST) de la valeur de  r''à 1.4 GHz. En effet, quand la
température augmente, la viscosité de l’eau de mer diminue et ainsi la conductivité ionique augmente,
contrairement à la polarisation dipolaire qui diminue. C’est la sensibilité de
r''à 1.4 GHz. En effet, quand la
température augmente, la viscosité de l’eau de mer diminue et ainsi la conductivité ionique augmente,
contrairement à la polarisation dipolaire qui diminue. C’est la sensibilité de  ion à la SSS qui détermine
principalement la sensibilité de
ion à la SSS qui détermine
principalement la sensibilité de  r à la SSS, et par conséquent celle des coefficients Rv et
Rh .
r à la SSS, et par conséquent celle des coefficients Rv et
Rh .
Quand la fréquence augmente, la sensibilité de  r''à
r''à  ion diminue et c’est alors la nature polaire des
molécules constituant l’eau de mer qui est à l’origine de l’absorption des ondes EM (phénomène de
polarisation par orientation dipolaire). L’atténuation par polarisation dipolaire est liée au retard
d’orientation des molécules polaires par rapport au champ électrique (voir l’annexe G). Le temps de
relaxation de l’eau de mer, qui traduit ce retard d’orientation des molécules, correspond à une fréquence
de relaxation variant de 10 GHz à 23 GHz entre 0oC et 30oC. Ainsi, à 1.4 GHz qui est une fréquence
beaucoup plus basse que la fréquence de relaxation, les molécules suivent relativement bien le champ
électrique ce qui explique que l’atténuation par polarisation dipolaire soit plus faible qu’à plus haute
fréquence.
ion diminue et c’est alors la nature polaire des
molécules constituant l’eau de mer qui est à l’origine de l’absorption des ondes EM (phénomène de
polarisation par orientation dipolaire). L’atténuation par polarisation dipolaire est liée au retard
d’orientation des molécules polaires par rapport au champ électrique (voir l’annexe G). Le temps de
relaxation de l’eau de mer, qui traduit ce retard d’orientation des molécules, correspond à une fréquence
de relaxation variant de 10 GHz à 23 GHz entre 0oC et 30oC. Ainsi, à 1.4 GHz qui est une fréquence
beaucoup plus basse que la fréquence de relaxation, les molécules suivent relativement bien le champ
électrique ce qui explique que l’atténuation par polarisation dipolaire soit plus faible qu’à plus haute
fréquence.
| | 0o C | 15oC | 30oC |
|
|
|
| | 30 psu | 2.52 | 3.74 | 5.09 |
| 35 psu | 2.91 | 4.29 | 5.83 |
| 40 psu | 3.29 | 4.84 | 6.57 |
|
|
|
| | |
| TAB. 4.1: | Conductivité ionique de l’eau de mer en fonction de la température et de la salinité,
d’après [47 ] |
|
La conductivité  ion dérivée du modèle KS ([47]) est reportée dans le tableau 4.1 pour différentes
températures et salinités. Elle est de 4.29 Sm-1 à 15oC et 35 psu et augmente quasi-linéairement avec la
salinité et la température, pour des salinités comprises entre 30 psu et 40 psu et des températures
comprises entre 0oC et 30oC. Les modèles ST95 et ST97 prédisent des conductivités similaires à celles
prédites par le modèle KS (i.e. elle diffèrent d’au plus 0.4%) dans la gamme 30-40 psu, alors que le modèle
EL prédit un
ion dérivée du modèle KS ([47]) est reportée dans le tableau 4.1 pour différentes
températures et salinités. Elle est de 4.29 Sm-1 à 15oC et 35 psu et augmente quasi-linéairement avec la
salinité et la température, pour des salinités comprises entre 30 psu et 40 psu et des températures
comprises entre 0oC et 30oC. Les modèles ST95 et ST97 prédisent des conductivités similaires à celles
prédites par le modèle KS (i.e. elle diffèrent d’au plus 0.4%) dans la gamme 30-40 psu, alors que le modèle
EL prédit un  ion systématiquement inférieur à celui prédit par le modèle KS, d’environ 2-4% (voir la
discussion précédente sur la paramétrisation de
ion systématiquement inférieur à celui prédit par le modèle KS, d’environ 2-4% (voir la
discussion précédente sur la paramétrisation de  ion par le modèle EL). Par conséquent, comme on peut
le constater sur les figures de l’annexe P (section 2),
ion par le modèle EL). Par conséquent, comme on peut
le constater sur les figures de l’annexe P (section 2),  '' diffère très peu (la différence est de
l’ordre de 0.35%) entre les modèle KS et ST95 pour les SST élevées auxquelles
'' diffère très peu (la différence est de
l’ordre de 0.35%) entre les modèle KS et ST95 pour les SST élevées auxquelles  ion prévaut,
alors que la différence entre les modèle KS et EL est de 2%. Cependant, les modèles ST97 et
ST95 prédisent un
ion prévaut,
alors que la différence entre les modèle KS et EL est de 2%. Cependant, les modèles ST97 et
ST95 prédisent un  ion sensiblement différent (i.e. différence ¿ 1%) de celui prédit par le
modèle KS pour des salinités inférieures à 6 psu. De telles salinités ne concernent pas la mission
SMOS.
ion sensiblement différent (i.e. différence ¿ 1%) de celui prédit par le
modèle KS pour des salinités inférieures à 6 psu. De telles salinités ne concernent pas la mission
SMOS.
 r est relié à la fréquence électromagnétique
r est relié à la fréquence électromagnétique  par une fonction
paramétrique dont les paramètres sont ajustés sur des mesures de constante diélectrique à différentes
températures et salinités (i.e. les paramètres dépendent de la température et de la salinité). La
fonction paramétrique est l’équation de relaxation, proposée par Debye ([18] pour les molécules
polaires, voir l’annexe G) à partir d’hypothèse physiques. On déduit de (2.5), (A.11) et (G.51),
l’équation à un temps de relaxation pour la constante diélectrique relative de l’eau de mer
suivante:
par une fonction
paramétrique dont les paramètres sont ajustés sur des mesures de constante diélectrique à différentes
températures et salinités (i.e. les paramètres dépendent de la température et de la salinité). La
fonction paramétrique est l’équation de relaxation, proposée par Debye ([18] pour les molécules
polaires, voir l’annexe G) à partir d’hypothèse physiques. On déduit de (2.5), (A.11) et (G.51),
l’équation à un temps de relaxation pour la constante diélectrique relative de l’eau de mer
suivante: