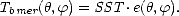
D’après (2.16), la Tb de l’océan (Tbmer) est reliée à l’émissivité par
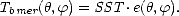 | (2.19) |
À l’équilibre thermodynamique, l’émissivité est égale à l’absorptivité a qui représente la fraction de puissance incidente à la surface de la mer qui est absorbée. On a donc

où R est le coefficient de réflexion de la surface.
La première difficulté pour estimer la SSS à partir d’un radiomètre, est de passer de la mesure de TA à
une estimation de la Tb de l’océan. Pour cela il faut corriger des effets du diagramme d’antenne, de la
contribution des autres sources et de la traversée de l’atmosphère (voir chapitre 6 et 7.2).
Une fois que l’on s’est ramené à une estimation de la Tb de l’océan, il faut inverser celle-ci
en SSS . Un modèle simple pour relier la Tb de l’océan à la SSS consiste à considérer que la
surface de la mer est plane et d’étendue infinie devant la longueur d’onde de l’instrument
 0 . Dans ce cas, la réflexion à la surface est spéculaire et R est le coefficient de réflexion de
Fresnel (R Fr ), qui dépend de l’angle d’incidence
0 . Dans ce cas, la réflexion à la surface est spéculaire et R est le coefficient de réflexion de
Fresnel (R Fr ), qui dépend de l’angle d’incidence  (pas de dépendance azimutale car dans ce
modèle simpliste la surface de la mer est isotrope) et de la permittivité
(pas de dépendance azimutale car dans ce
modèle simpliste la surface de la mer est isotrope) et de la permittivité  de l’eau de mer. On a
ainsi
de l’eau de mer. On a
ainsi
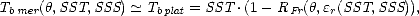 | (2.22) |
où T bplat est la température de brillance d’une surface plane. Les coefficients de reflexion de la surface en polarisations verticale (Rv) et horizontale (Rh) (voir le chapitre 4.1 pour la définition des polarisations d’une onde EM) sont donnés par les coefficients de Fresnel ([90 , 87 ])
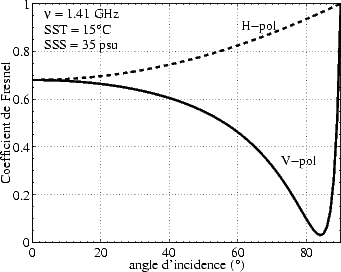
La variation de ces coefficients en fonction de  , pour une SSS et une SST moyennes, à la
fréquence de 1.4 GHz est reporté sur la figure 2.4. La variation du coefficient de réflexion
dépend de la polarisation: Rh est de l’ordre de 0.7 au nadir (i.e. à
, pour une SSS et une SST moyennes, à la
fréquence de 1.4 GHz est reporté sur la figure 2.4. La variation du coefficient de réflexion
dépend de la polarisation: Rh est de l’ordre de 0.7 au nadir (i.e. à  = 0o) et croît avec
= 0o) et croît avec  croissant jusqu’à 1 à
croissant jusqu’à 1 à  = 90o (i.e. incidence rasante) alors que Rv (qui vaut aussi 0.7 au nadir)
décroît avec
= 90o (i.e. incidence rasante) alors que Rv (qui vaut aussi 0.7 au nadir)
décroît avec  croissant jusqu’à un angle
croissant jusqu’à un angle  B
B 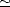 84o. Cet angle
84o. Cet angle  B pour lequel Rv passe par un
minimum proche de 0 est l’angle de Brewster. On peut vérifier à partir de (2.23) que pour
les milieux dont la permittivité est réelle (i.e. milieux sans pertes), à l’angle
B pour lequel Rv passe par un
minimum proche de 0 est l’angle de Brewster. On peut vérifier à partir de (2.23) que pour
les milieux dont la permittivité est réelle (i.e. milieux sans pertes), à l’angle  B, l’onde en
polarisation verticale onde n’est pas réfléchie (i.e. Rv passe par un minimum nul), et donc que le
rayonnent réfléchi est totalement polarisé horizontalement (tan
B, l’onde en
polarisation verticale onde n’est pas réfléchie (i.e. Rv passe par un minimum nul), et donc que le
rayonnent réfléchi est totalement polarisé horizontalement (tan B =
B = 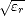 pour un milieu
sans pertes). Aux angles d’incidence supérieurs à
pour un milieu
sans pertes). Aux angles d’incidence supérieurs à  B, Rv croît avec
B, Rv croît avec  jusqu’à 1 à incidence
rasante. Ceci se traduit par une emissivité de l’ordre de 0.3 pour les deux polarisations au
nadir1 ,
qui diminue en polarisation horizontale jusqu’à valoir 0 à incidence rasante, et qui augmente en
polarisation verticale jusqu’à l’angle de Brewster où elle sera proche de 1, avant de chuter vers 0 à
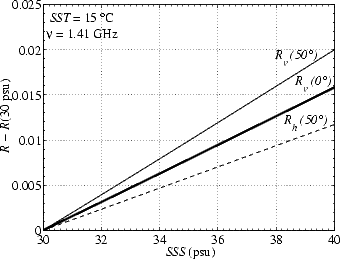
incidence rasante. La figure 2.5 illustre la variation des coefficients de Fresnel avec la SSS pour une SST
de 15o C. On constate qu’elle est relativement faible, de l’ordre de 1.5×10-3 par psu, et qu’elle
augmente en polarisation verticale quand
jusqu’à 1 à incidence
rasante. Ceci se traduit par une emissivité de l’ordre de 0.3 pour les deux polarisations au
nadir1 ,
qui diminue en polarisation horizontale jusqu’à valoir 0 à incidence rasante, et qui augmente en
polarisation verticale jusqu’à l’angle de Brewster où elle sera proche de 1, avant de chuter vers 0 à
incidence rasante. La figure 2.5 illustre la variation des coefficients de Fresnel avec la SSS pour une SST
de 15o C. On constate qu’elle est relativement faible, de l’ordre de 1.5×10-3 par psu, et qu’elle
augmente en polarisation verticale quand  augmente alors qu’elle diminue en polarisation
horizontale. Il faut noter aussi que la sensibilité de Rv et Rh varie avec la SST (non montré) ;
la sensibilité de Tbmer aux différents paramètres géophysiques est détaillée dans la section
4.6.
augmente alors qu’elle diminue en polarisation
horizontale. Il faut noter aussi que la sensibilité de Rv et Rh varie avec la SST (non montré) ;
la sensibilité de Tbmer aux différents paramètres géophysiques est détaillée dans la section
4.6.
|
|
|
|
Pour restituer la SSS à partir de la Tb, il faut connaître précisément la dépendance de  à la SSS et à
la SST en bande L (voir sections 4.2 et 5.1). De plus, même si la relation entre
à la SSS et à
la SST en bande L (voir sections 4.2 et 5.1). De plus, même si la relation entre  r et la SSS et la SST était
parfaitement connue, il resterait une incertitude sur la SSS estimée résultant des incertitudes sur la
mesure de la SST et de la Tb. Il en résulte une incertitude sur la SSS restituée qu’il faut évaluer (voir
section 5.2). Enfin, le modèle décrit par (2.22) est très insuffisant pour estimer la Tb de l’océan car
la surface océanique n’est pas plane et la Tb est sensible à la structure de la surface (voir
section 4.6). Le coefficient R doit donc prendre en compte des paramètres comme le vecteur
vent à la surface de l’océan, la quantité et l’émissivité de l’écume, la présence de houle, etc
...
r et la SSS et la SST était
parfaitement connue, il resterait une incertitude sur la SSS estimée résultant des incertitudes sur la
mesure de la SST et de la Tb. Il en résulte une incertitude sur la SSS restituée qu’il faut évaluer (voir
section 5.2). Enfin, le modèle décrit par (2.22) est très insuffisant pour estimer la Tb de l’océan car
la surface océanique n’est pas plane et la Tb est sensible à la structure de la surface (voir
section 4.6). Le coefficient R doit donc prendre en compte des paramètres comme le vecteur
vent à la surface de l’océan, la quantité et l’émissivité de l’écume, la présence de houle, etc
...
On voit qu’il existe plusieurs sources d’incertitude lors de l’estimation de la SSS à partir de mesures radiométriques. Je traiterai principalement dans cette thèse des questions relatives à la modélisation de la T b de l’océan en bande L. J’exposerai aussi plus succintement les problèmes des sources parasites et de la traversée de l’atmosphère. Concernant le bruit instrumental sur la mesure de la Tbpar SMOS, j’utiliserai les estimation effectuées par P. Waldteufel (voir chapitres 3.1 et 5.2).