L’erreur sur une mesure radiométrique individuelle de MIRAS est supérieure à 1 K, ce qui implique que
l’incertitude sur la SSS inversée à partir d’une mesure individuelle de Tb peut être supérieure
à 5 psu (voir la section 4.6). Une telle incertitude rend les mesures SMOS peu utilisables
pour la plupart des applications, la précision recherchée sur la SSS étant inférieure au psu et
idéalement de 0.1 psu (voir la section 1.2). Pour améliorer la précision sur la SSS, on peut
heureusement améliorer la précision radiométrique de SMOS en combinant plusieurs mesures
indépendantes et moyenner les estimations de SSS sur des échelles spatio-temporelles plus grandes
que celles de la mesure. Une étude concernant l’incertitude sur la SSS restituée à partir des
mesures SMOS est décrite dans l’article reproduit en section 5.2.3. Elle est résumée dans cette
section.
Pour réduire l’erreur radiométrique, on dispose de plusieurs estimations indépendantes de Tbmer en un
point donné. En se déplaçant sur son orbite, MIRAS prendra des images successives de l’océan
décalées spatialement dans la direction de la trace sub-satellite (voir la section 3). Un point de
l’océan va donc se déplacer le long d’une ligne dans le champ de vue de l’instrument, que
j’appelle la ligne de mesure (dwell line, voir la figure 3.7). Le long de cette ligne de mesure, N
mesures du même point de la surface océanique sont effectuées à différents angles d’incidence. N
dépend de l’écart entre la ligne de mesure et la trace sub-satellite, c’est à dire de l’abscisse
sur la figure 3.5. N est d’autant plus grand que l’on est proche de la trace sub-satellite. Ces
N estimations de Tbmer vont ensuite être combinées pour estimer une SSS ”élémentaire”,
c’est à dire une SSS instantanée sur un pixel dont la taille typique est de 40 km. Les sections
5.2.1 et 5.2.2 décrivent la méthode d’inversion, proposée par Jackson ([42], que nous avons
utilisée.
On peut améliorer la précision sur la SSS estimée en effectuant une moyenne spatio-temporelle des
SSSélémentaires (i.e. des SSS instantanée de résolution 40 km). Il s’agit alors de faire le meilleur
compromis entre la précision sur la SSS et la résolution spatio-temporelle. Nous avons effectué une
moyenne sur des pavés de 200 km x 200 km et sur 10 jours, en nous basant sur les recommandations
GODAE (voir le chapitre 1.2).
Pour le calcul d’erreur, nous avons supposé que nous connaissions la SST avec une précision de 1oC et
que la T b était mesurée avec la précision donnée en (3.1). Plusieurs scénarii ont été étudiés concernant
l’erreur sur l’estimation du vent: vent totalement inconnu (erreur infinie), vent moyen sur 10 jours connu
(l’erreur est alors la combinaison de l’erreur de la mesure et de la variabilité temporelle du vent) et vent
instantané connu (erreur de la mesure). L’absence totale de connaissance du vent ou l’utilisation d’un
vent moyen sur 10 jours conduit à des erreurs en SSS aux hautes latitudes respectivement de l’ordre
de 0.15 et de 0.1 psu qui ne sont pas compatibles avec la précision recherchée. Aux hautes
latitudes, où la variabilité temporelle du vent est grande, les SSS inversées en utilisant un vent
instantané sont jusqu’à deux fois plus précises que celles déduites des mesures de vent moyennées
sur 10 jours. Ceci montre l’importance de l’utilisation de données de vent à haute résolution
temporelle dans les zones à forte variabilité temporelle. Par contre, aux basses latitudes, où la
variabilité temporelle du vent est faible, l’utilisation du vent moyen conduit à des précisions
légèrement supérieures à celles obtenues avec le vent instantané. En effet, la diminution de
l’erreur de mesure du vent par moyennage l’emporte sur l’augmentation de l’erreur créée
par la variabilité temporelle. Par ailleurs, nous avons estimé que la variabilité spatiale du
vent à l’échelle de 200 km était négligeable, contrairement à sa variabilité temporelle sur 10
jours.
Nous avons étudié la possibilité de supprimer l’erreur de mesure causée par l’effet Faraday en utilisant
T1 = Tv + Th pour inverser la SSS. Comme on dispose de deux fois moins d’estimations de la Tb en
utilisant T1 à la place de Tv et Th séparemment, l’erreur sur l’estimation de la SSS devrait
être accrue par un facteur 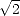 . Ce n’est pas le cas car la sensibilité de T1 à la SSS est de
l’ordre de deux fois plus grande que celles de Tv et de Th. Par conséquent la précision sur
la SSS est peu dégradée lorsque l’on utilise T1, qui a l’avantage d’être insensible à l’effet
Faraday.
. Ce n’est pas le cas car la sensibilité de T1 à la SSS est de
l’ordre de deux fois plus grande que celles de Tv et de Th. Par conséquent la précision sur
la SSS est peu dégradée lorsque l’on utilise T1, qui a l’avantage d’être insensible à l’effet
Faraday.
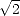 . Ce n’est pas le cas car la sensibilité de T1 à la SSS est de
l’ordre de deux fois plus grande que celles de Tv et de Th. Par conséquent la précision sur
la SSS est peu dégradée lorsque l’on utilise T1, qui a l’avantage d’être insensible à l’effet
Faraday.
. Ce n’est pas le cas car la sensibilité de T1 à la SSS est de
l’ordre de deux fois plus grande que celles de Tv et de Th. Par conséquent la précision sur
la SSS est peu dégradée lorsque l’on utilise T1, qui a l’avantage d’être insensible à l’effet
Faraday.