![[Tb1,Tb2,...,TbN],](plan_html466x.gif)
![[Tb1,Tb2,...,TbN],](plan_html466x.gif) |
du même pixel vu sous N angles d’incidence différents
![[h1,h2,...,hN ],](plan_html467x.gif) |
avec des erreurs de mesure sur Tb (en écart type)
![[sT1,sT2,...,sTN ].](plan_html468x.gif) |
On suppose que l’on a aussi une estimation initiale du paramètre exogène SST, et dans certains des
scénarii de U, que l’on appelle respectivement (SST)0 et (U)0 (ces estimations peuvent provenir de
mesures satellitales ou de modèles météorologiques). Les incertitudes respectives sur ces paramètres
initiaux sont  U et
U et  SST. On cherche alors à déterminer la SSS et son incertitude
SST. On cherche alors à déterminer la SSS et son incertitude  SSS par un processus
itératif. On commence par fixer une estimation initiale de la SSS (dans notre cas (SSS)0 = 34 psu). Nous
n’avons pas observé d’influence notable de (SSS)0 sur le résultat de l’inversion, mais elle influence un
peu la rapidité de convergence du calcul. On obtient à partir du modèle direct d’émissivité
décrit dans le chapitre 4, une estimation initiale des N températures de brillance donnée
par
SSS par un processus
itératif. On commence par fixer une estimation initiale de la SSS (dans notre cas (SSS)0 = 34 psu). Nous
n’avons pas observé d’influence notable de (SSS)0 sur le résultat de l’inversion, mais elle influence un
peu la rapidité de convergence du calcul. On obtient à partir du modèle direct d’émissivité
décrit dans le chapitre 4, une estimation initiale des N températures de brillance donnée
par
![(T ) = f [(SST) ,(U ) ,(SSS) ,h].
bi 0 0 0 0 i](plan_html469x.gif) |
De ces estimations, on dérive les écarts 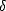 Tbi entre les Tb estimées ((Tbi)0) et les Tb mesurées définis
comme
Tbi entre les Tb estimées ((Tbi)0) et les Tb mesurées définis
comme
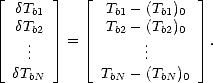 |
En posant 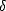 SSS = SSS - (SSS)0,
SSS = SSS - (SSS)0, 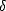 SST = SST - (SST)0 et
SST = SST - (SST)0 et 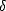 U = U - (U)0, on a
U = U - (U)0, on a
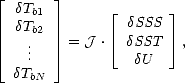 |
où J est la matrice jacobienne au point ![[(SST)0,(U )0,(SSS)0]](plan_html472x.gif) donnée par
donnée par
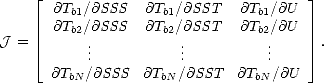 |
En utilisant aussi la SST et U comme des mesures indépendantes au même titre que les Tbi, on obtient les systèmes suivants
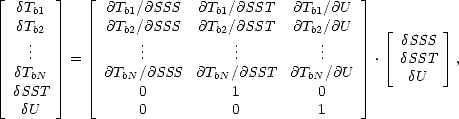 |
que l’on normalise par les écarts types pour le résoudre au sens des moindres carrés. On a alors
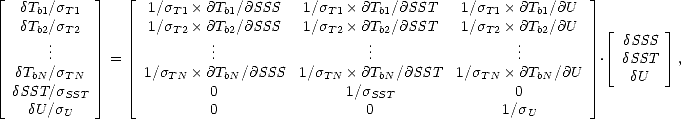 |
que l’on réécrit
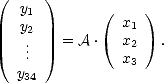 |
À l’état initial, on a y33 = y34 = 0 car SST = (SST)0 et U = (U)0. (SST)0 à la surface du globe est
déduite de la climatologie Reynolds ([76]) (voir la figure 4 de l’article section 5.2.3) et (U)0 est déduit
des mesures satellitales QSCAT illustrées sur la figure 4.38 (bas). L’incertitude sur la SST
est fixée à  SST = 1oC. L’incertitude sur le vent dépend du scénario envisagé (voir l’article
section 5.2.3) ; si l’on dispose de vents instantanés,
SST = 1oC. L’incertitude sur le vent dépend du scénario envisagé (voir l’article
section 5.2.3) ; si l’on dispose de vents instantanés,  U est de 1.5 m.s-1 pour 3 m.s-1 < U < 15
m.s-1 , de 2 m.s-1 pour U < 3 m.s-1 et de 10% de U pour U > 15 m.s-1. Si l’on utilise une
moyenne sur 10 jours et 200x200 km2,
U est de 1.5 m.s-1 pour 3 m.s-1 < U < 15
m.s-1 , de 2 m.s-1 pour U < 3 m.s-1 et de 10% de U pour U > 15 m.s-1. Si l’on utilise une
moyenne sur 10 jours et 200x200 km2,  U est une combinaison de l’erreur précédente et de la
variabilité du vent sur 10 jours, 200x200 km2 deduite de l’écart type des mesures de vents par
le satellite QSCAT (figure 7 de l’article). La matrice A est calculée avec le modèle direct
d’émissivité. On résoud alors le système pour obtenir
U est une combinaison de l’erreur précédente et de la
variabilité du vent sur 10 jours, 200x200 km2 deduite de l’écart type des mesures de vents par
le satellite QSCAT (figure 7 de l’article). La matrice A est calculée avec le modèle direct
d’émissivité. On résoud alors le système pour obtenir 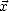 avec la méthode exposée dans l’annexe
O. À partir de
avec la méthode exposée dans l’annexe
O. À partir de 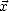 , on réévalue la SSS, la SST et U et on obtient de nouvelles estimations
, on réévalue la SSS, la SST et U et on obtient de nouvelles estimations
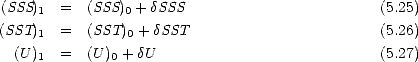
![(Tbi)1 = f [(SST)1,(U )1,(SSS)1,hi].](plan_html480x.gif)
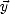 , pour lequel on va chercher un nouvelle solution
, pour lequel on va chercher un nouvelle solution 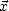 . On itère ainsi jusqu’à ce que la
méthode ait convergée, c’est à dire jusqu’à ce que
. On itère ainsi jusqu’à ce que la
méthode ait convergée, c’est à dire jusqu’à ce que
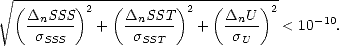 | (5.28) |
où  n X = (X)n - (X)n-1 représente la correction apportée à la variable X à la nième itération sur sa
valeur après la (n - 1)ième itération.
n X = (X)n - (X)n-1 représente la correction apportée à la variable X à la nième itération sur sa
valeur après la (n - 1)ième itération.