
 T dépendant des caractéristiques de l’instrument (voir la section 3.1), et que
l’on cherche à inverser en SSS. On a pour cela, à un angle d’incidence et une polarisation
donnés,
T dépendant des caractéristiques de l’instrument (voir la section 3.1), et que
l’on cherche à inverser en SSS. On a pour cela, à un angle d’incidence et une polarisation
donnés,
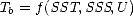 |
où la SST et U sont des variables exogènes estimées avec des incertitudes respectives  SST et
SST et  U et f
est la fonction étudiée dans le chapitre 4. On a alors, dans le cas d’une restitution de la SSS à partir d’une
seule mesure de Tb,
U et f
est la fonction étudiée dans le chapitre 4. On a alors, dans le cas d’une restitution de la SSS à partir d’une
seule mesure de Tb,
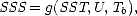 |
où g = f-1 est la fonction inverse de f.
On définit un point (SSS)0 = g((SST)0,(U)0,(Tb)0) autour duquel on va linéariser la fonction g par un développement de Taylor. On détermine ainsi le point SSS = g(SST,U,Tb) par
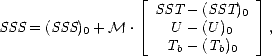 |
d’où
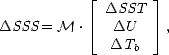 |
où  SSS = SSS - (SSS)0,
SSS = SSS - (SSS)0,  SST = SST - (SST)0,
SST = SST - (SST)0,  U = U - (U)0,
U = U - (U)0,  Tb = Tb - (Tb)0
et
Tb = Tb - (Tb)0
et
![M = [@g/@SST,@g/@U,@g/@Tb]](plan_html461x.gif) |
.
On peut alors déterminer  SSS, l’incertitude sur la SSS inversée, à partir des incertitudes
SSS, l’incertitude sur la SSS inversée, à partir des incertitudes  SST,
SST,  U et
U et
 T . On suppose que la SST, U et Tb sont des variables aléatoires indépendantes, ce qui nous donne la
matrice de covariance suivante
T . On suppose que la SST, U et Tb sont des variables aléatoires indépendantes, ce qui nous donne la
matrice de covariance suivante
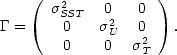 |
On obtient ainsi, d’après l’annexe N,
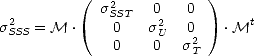 |
soit
![( ) |_ _|
2[ ] s2SST 0 0 @g/@SST
sSSS= @g/@SST @g/@U @g/@Tb . 0 s2U 0 . |_ @g/@U _| .
0 0 s2T @g/@Tb](plan_html464x.gif) |
On a donc l’expression suivante pour l’incertitude sur la SSS inversée à partir de variables aléatoires indépendantes
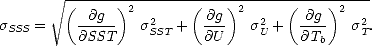 |