J’ai montré dans la section 4 que la rugosité de surface avait un effet important sur Tbmer, et que cet
effet dépend principalement des vagues dont la taille est proche de celle de  0, ainsi que de la variance des
pentes des grandes vagues lorsque
0, ainsi que de la variance des
pentes des grandes vagues lorsque  augmente. J’ai testé plusieurs paramétrisations du spectre des vagues
pour déterminer l’incertitude sur Tbmer due à l’incertitude sur la modélisation de l’état de mer. Le
modèle proposé par Elfouhaily et al. ([31]) est illustré pour plusieurs vents et une mer pleinement
développée (i.e.
augmente. J’ai testé plusieurs paramétrisations du spectre des vagues
pour déterminer l’incertitude sur Tbmer due à l’incertitude sur la modélisation de l’état de mer. Le
modèle proposé par Elfouhaily et al. ([31]) est illustré pour plusieurs vents et une mer pleinement
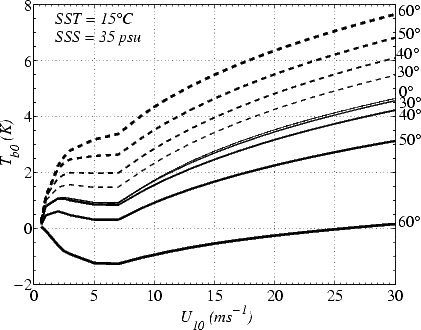
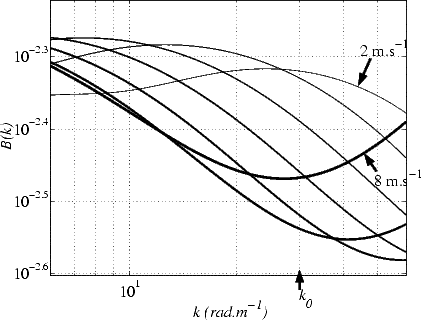
développée (i.e. 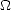 = 0.84) sur la figure 5.1, les figures dans [31] étant tracé pour
= 0.84) sur la figure 5.1, les figures dans [31] étant tracé pour 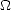 = 1. Les amplitudes
des harmoniques d’ordre zéro et deux du spectre de courbure 2D (respectivement C0(k) et
C2 (k)) sont illustrées pour U10 = 10 m.s-1 et pour les modèles DV, DV2 et ELF sur la figure
5.2. Près de k0 , le modèle ELF s’intercale entre les modèles DV et DV2 pour la composante
omnidirectionnelle. Pour la seconde harmonique, le modèle ELF est au dessus des deux autres dans la
région du k0 . Sur la figure 5.3 est représentée la fonction
= 1. Les amplitudes
des harmoniques d’ordre zéro et deux du spectre de courbure 2D (respectivement C0(k) et
C2 (k)) sont illustrées pour U10 = 10 m.s-1 et pour les modèles DV, DV2 et ELF sur la figure
5.2. Près de k0 , le modèle ELF s’intercale entre les modèles DV et DV2 pour la composante
omnidirectionnelle. Pour la seconde harmonique, le modèle ELF est au dessus des deux autres dans la
région du k0 . Sur la figure 5.3 est représentée la fonction  (k), qui traduit le rapport entre la
seconde harmonique et l’harmonique 0 du spectre. À 21 cm,
(k), qui traduit le rapport entre la
seconde harmonique et l’harmonique 0 du spectre. À 21 cm,  (k) est beaucoup plus forte (de
l’ordre d’un facteur trois) pour le modèle ELF que pour le modèle DV. À cette longueur
d’onde, on note que pour les deux modèles étudiés,
(k) est beaucoup plus forte (de
l’ordre d’un facteur trois) pour le modèle ELF que pour le modèle DV. À cette longueur
d’onde, on note que pour les deux modèles étudiés,  (k) dépend peu du vent et est plus faible
qu’à plus haute fréquence. Ceci signifie que la sensibilité au vent sera la même, en relatif,
que pour l’harmonique 0 et que la variation azimutale sera plus faible qu’à haute fréquence.
Dans les basses fréquences enfin, la valeur de
(k) dépend peu du vent et est plus faible
qu’à plus haute fréquence. Ceci signifie que la sensibilité au vent sera la même, en relatif,
que pour l’harmonique 0 et que la variation azimutale sera plus faible qu’à haute fréquence.
Dans les basses fréquences enfin, la valeur de  (k) (qui détermine la variance des pentes des
grandes vagues) est quasiment nulle pour le modèle DV alors qu’elle très grande pour le modèle
ELF.
(k) (qui détermine la variance des pentes des
grandes vagues) est quasiment nulle pour le modèle DV alors qu’elle très grande pour le modèle
ELF.
La figure 5.4 illustre le Tb,0 déduit du modèle de spectre ELF pour plusieurs incidences. La variation
avec le vent est très différente de celle déduite des modèles DV et DV2 (voir la figure 4.47), à la fois en
amplitude et en forme (voir aussi l’article en annexe Q). Entre 3 m.s-1 et 7 m.s-1, il y a un plateau,
d’autant plus marqué que l’angle d’incidence est faible. Ce plateau s’explique par le fait que pour
les vagues de la dizaine de centimètre à un mètre, l’amplitude du spectre diminue quand le
vent croît de 3 m.s-1 à 7 m.s-1 (voir la figure 5.5). Ainsi, l’influence des petites vagues, qui
est dominante pour les incidences faibles, diminue quand le vent croît dans cette gamme de
vent.
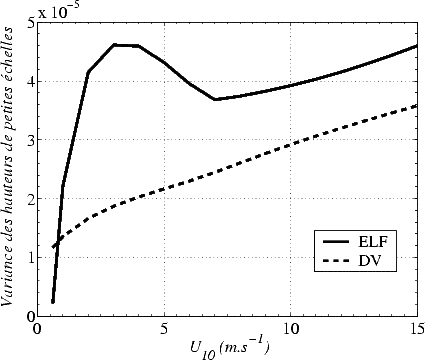
J’ai reporté sur la figure 5.6 la variance des hauteurs des petites vagues pour les spectres ELF et DV,
qui indique qualitativement l’influence des PE sur la Tbmer. On y constate l’inversion de l’effet du vent
sur les petites échelles dans la gamme de vents de 3 m.s-1 à 7 m.s -1 pour le modèle ELF,
alors que le modèle DV varie de manière monotone avec le vent. On peut voir aussi la très
forte sensibilité au vent du modèle ELF dans la gamme des vents faibles, et l’on note que
la sensibilité au vent est comparable pour les deux modèles pour des vents supérieurs à 7
m.s-1 .
J’ai reporté sur la figure 5.7 la variance des pentes des grandes vagues pour le spectre ELF, ainsi que
la variance des pentes de toutes les vagues. La variance des pentes des grandes vagues croît toujours avec
le vent, même dans la gamme 3 m.s-1 à 7 m.s-1. Par conséquent, l’effet des grandes vagues va compenser
celui des petites vagues et atténuer l’effet de plateau. Ainsi, plus l’angle d’incidence augmente, moins le
plateau est prononcé car la part relative de l’effet des grandes vagues augmente. On verra dans la section
7.3 que ce plateau est peu crédible. On peut remarquer aussi que la variance des pentes des grandes
vagues est anisotrope pour le modèle ELF, contrairement au modèle DV (voir la figure 4.21).
Ceci s’explique par le fait que le  (k) est grand aux basses fréquences pour le spectre EL,
alors qu’il est quasiment nul pour le spectre DV. Enfin, on voit que la variance des pentes
calculée pour toutes les vagues subit une inflexion en fonction du vent, ceci à cause des vagues
décimétriques.
(k) est grand aux basses fréquences pour le spectre EL,
alors qu’il est quasiment nul pour le spectre DV. Enfin, on voit que la variance des pentes
calculée pour toutes les vagues subit une inflexion en fonction du vent, ceci à cause des vagues
décimétriques.
J’ai reporté sur les figures 5.8, 5.9 et 5.10 les amplitudes des harmoniques 0, 1 et 2 des Tbmer déduites
des trois modèles de spectre pour un vent de 10 m.s-1 (relativement loin du plateau). L’effet du vent sur
la T bmer omnidirectionnelle dépend beaucoup du modèle de spectre. Il est évidemment doublé entre les
modèles DV et DV2. Le modèle ELF se situe entre les deux autres. Par contre, le modèle ELF prédit une
Tb,2beaucoup plus forte que celle prédite par les modèles DV et DV2, à cause d’une valeur de  (k) plus
élevée vers 21 cm pour le spectre ELF que pour les autres spectres. Cependant, les modèles
s’accordent sur le fait que la deuxième harmonique en bande L est plus faible qu’à plus haute
fréquence.
(k) plus
élevée vers 21 cm pour le spectre ELF que pour les autres spectres. Cependant, les modèles
s’accordent sur le fait que la deuxième harmonique en bande L est plus faible qu’à plus haute
fréquence.
Les différents modèles de spectres induisent des écarts sur la composante omnidirectionnelle et sur la
variation azimutale de Tbmer. Les différences sur la composante omnidirectionnelle de Tbmer sont grandes,
à la fois sur l’amplitude de la variation de Tbmer avec le vent, mais aussi sur sa forme. Des mesures de
Tbmeren bande L devraient permettre de déterminer la validité de ces différents modèles
en ce qui concerne leur influence sur Tb,0. La variation azimutale de Tbmer vaut, selon les
modèles, de moins de 0.1 K à quelques dixièmes de Kelvins. Par conséquent, la validation du
modèle de spectre pour ce qui concerne la variation azimutale exige une très grande précision
radiométrique.
 0, ainsi que de la variance des
pentes des grandes vagues lorsque
0, ainsi que de la variance des
pentes des grandes vagues lorsque  augmente. J’ai testé plusieurs paramétrisations du spectre des vagues
pour déterminer l’incertitude sur Tbmer due à l’incertitude sur la modélisation de l’état de mer. Le
modèle proposé par Elfouhaily et al. ([31]) est illustré pour plusieurs vents et une mer pleinement
développée (i.e.
augmente. J’ai testé plusieurs paramétrisations du spectre des vagues
pour déterminer l’incertitude sur Tbmer due à l’incertitude sur la modélisation de l’état de mer. Le
modèle proposé par Elfouhaily et al. ([31]) est illustré pour plusieurs vents et une mer pleinement
développée (i.e. 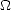 = 0.84) sur la figure 5.1, les figures dans [31] étant tracé pour
= 0.84) sur la figure 5.1, les figures dans [31] étant tracé pour 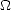 = 1. Les amplitudes
des harmoniques d’ordre zéro et deux du spectre de courbure 2D (respectivement C0(k) et
C2 (k)) sont illustrées pour U10 = 10 m.s-1 et pour les modèles DV, DV2 et ELF sur la figure
5.2. Près de k0 , le modèle ELF s’intercale entre les modèles DV et DV2 pour la composante
omnidirectionnelle. Pour la seconde harmonique, le modèle ELF est au dessus des deux autres dans la
région du k0 . Sur la figure 5.3 est représentée la fonction
= 1. Les amplitudes
des harmoniques d’ordre zéro et deux du spectre de courbure 2D (respectivement C0(k) et
C2 (k)) sont illustrées pour U10 = 10 m.s-1 et pour les modèles DV, DV2 et ELF sur la figure
5.2. Près de k0 , le modèle ELF s’intercale entre les modèles DV et DV2 pour la composante
omnidirectionnelle. Pour la seconde harmonique, le modèle ELF est au dessus des deux autres dans la
région du k0 . Sur la figure 5.3 est représentée la fonction  (k), qui traduit le rapport entre la
seconde harmonique et l’harmonique 0 du spectre. À 21 cm,
(k), qui traduit le rapport entre la
seconde harmonique et l’harmonique 0 du spectre. À 21 cm,  (k) est beaucoup plus forte (de
l’ordre d’un facteur trois) pour le modèle ELF que pour le modèle DV. À cette longueur
d’onde, on note que pour les deux modèles étudiés,
(k) est beaucoup plus forte (de
l’ordre d’un facteur trois) pour le modèle ELF que pour le modèle DV. À cette longueur
d’onde, on note que pour les deux modèles étudiés,  (k) dépend peu du vent et est plus faible
qu’à plus haute fréquence. Ceci signifie que la sensibilité au vent sera la même, en relatif,
que pour l’harmonique 0 et que la variation azimutale sera plus faible qu’à haute fréquence.
Dans les basses fréquences enfin, la valeur de
(k) dépend peu du vent et est plus faible
qu’à plus haute fréquence. Ceci signifie que la sensibilité au vent sera la même, en relatif,
que pour l’harmonique 0 et que la variation azimutale sera plus faible qu’à haute fréquence.
Dans les basses fréquences enfin, la valeur de  (k) (qui détermine la variance des pentes des
grandes vagues) est quasiment nulle pour le modèle DV alors qu’elle très grande pour le modèle
ELF.
(k) (qui détermine la variance des pentes des
grandes vagues) est quasiment nulle pour le modèle DV alors qu’elle très grande pour le modèle
ELF.
 (k) est grand aux basses fréquences pour le spectre EL,
alors qu’il est quasiment nul pour le spectre DV. Enfin, on voit que la variance des pentes
calculée pour toutes les vagues subit une inflexion en fonction du vent, ceci à cause des vagues
décimétriques.
(k) est grand aux basses fréquences pour le spectre EL,
alors qu’il est quasiment nul pour le spectre DV. Enfin, on voit que la variance des pentes
calculée pour toutes les vagues subit une inflexion en fonction du vent, ceci à cause des vagues
décimétriques.
 (k) plus
élevée vers 21 cm pour le spectre ELF que pour les autres spectres. Cependant, les modèles
s’accordent sur le fait que la deuxième harmonique en bande L est plus faible qu’à plus haute
fréquence.
(k) plus
élevée vers 21 cm pour le spectre ELF que pour les autres spectres. Cependant, les modèles
s’accordent sur le fait que la deuxième harmonique en bande L est plus faible qu’à plus haute
fréquence.