La rugosité de la surface océanique résulte de l’action du vent. Pour étudier Tbmer induite par le vent (i.e.
Tbvent), je vais la décomposer en série de Fourier de l’angle d’azimut  0 par rapport au vent, comme
cela a été fait pour le spectre de la mer du vent (section 4.3.4) et pour les coefficients de
diffusion (section 4.4). Pour les V- et H-pol, on ne conserve que les termes pairs car Tbvent est
symétrique par rapport à
0 par rapport au vent, comme
cela a été fait pour le spectre de la mer du vent (section 4.3.4) et pour les coefficients de
diffusion (section 4.4). Pour les V- et H-pol, on ne conserve que les termes pairs car Tbvent est
symétrique par rapport à 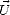 ([105]). On a ainsi respectivement en polarisations verticale et
horizontale
([105]). On a ainsi respectivement en polarisations verticale et
horizontale
où T b,0 est la Tbvent omnidirectionnelle, c’est à dire celle moyennée sur toutes les directions
azimutales, et où Tb,1 et Tb,2 traduisent respectivement les asymétries upwind/downwind et
upwind/crosswind de Tbvent. De même, T3 et T4 sont décomposés en une série de Fourier de termes
impaires
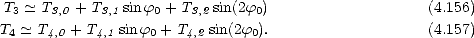
Une telle décomposition n’est pas applicable si toutes les échelles de rugosité ne sont pas symétriques
par rapport à 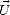 . Long et Drinkwater ([56]) ont montré sur des données diffusiométriques (ERS et
NSCAT) et radiométriques (SSM/I) acquises au dessus du continent Antarctique que la modulation des
petites rugosités à la surface des glaces par les grandes pentes donnait lieu a des variations
azimutales très différentes de celles des expressions (4.154, 4.155, 4.156 et 4.157). Dans le cas
de l’océan, il peut aussi y avoir une partie des grandes vagues dont l’orientation diffère de
celles des petites vagues. Ces vagues ne sont donc pas induites par le vent local et présent ;
soit elles proviennent d’un autre lieu, soit elles sont le résidu d’une ancienne mer du vent.
C’est le phénomène de houle. Par conséquent, les vagues de houle ne sont pas décrites par le
modèle de spectre de la mer du vent de la section 4.3.4. L’effet de la houle sur la variation
azimutale pourrait être similaire à celui présenté par Long et Drinkwater. C’est pourquoi
j’ai quantifié l’ordre de grandeur de l’effet de la houle sur Tbmer, et particulièrement d’une
houle non alignée avec le vent local, en utilisant le modèle décrit dans la section 4.3.9. J’ai
montré que l’effet de la houle est négligeable car il est inférieur à 0.1 K sur la compsante
omnidirectionnelle et il est encore plus faible sur les harmoniques 1 et 2 (voir la section 4.6.4).
Par conséquent, je vais supposer dans cette section que la surface n’est influencée que par le
vent local, c’est à dire qu’il n’y a pas de houle. L’état de la surface océanique est modélisé
par le spectre de mer du vent décrit dans la section 4.3.4, c’est-à-dire le modèle DV2. La
valeur du CDN est dérivé de (4.75) et (4.77) avec z0 derivé du modèle Pierson76 donné par
(4.83). Le modèle KS est utilisé pour la constante diélectrique. L’écume n’est pas prise en
compte.
. Long et Drinkwater ([56]) ont montré sur des données diffusiométriques (ERS et
NSCAT) et radiométriques (SSM/I) acquises au dessus du continent Antarctique que la modulation des
petites rugosités à la surface des glaces par les grandes pentes donnait lieu a des variations
azimutales très différentes de celles des expressions (4.154, 4.155, 4.156 et 4.157). Dans le cas
de l’océan, il peut aussi y avoir une partie des grandes vagues dont l’orientation diffère de
celles des petites vagues. Ces vagues ne sont donc pas induites par le vent local et présent ;
soit elles proviennent d’un autre lieu, soit elles sont le résidu d’une ancienne mer du vent.
C’est le phénomène de houle. Par conséquent, les vagues de houle ne sont pas décrites par le
modèle de spectre de la mer du vent de la section 4.3.4. L’effet de la houle sur la variation
azimutale pourrait être similaire à celui présenté par Long et Drinkwater. C’est pourquoi
j’ai quantifié l’ordre de grandeur de l’effet de la houle sur Tbmer, et particulièrement d’une
houle non alignée avec le vent local, en utilisant le modèle décrit dans la section 4.3.9. J’ai
montré que l’effet de la houle est négligeable car il est inférieur à 0.1 K sur la compsante
omnidirectionnelle et il est encore plus faible sur les harmoniques 1 et 2 (voir la section 4.6.4).
Par conséquent, je vais supposer dans cette section que la surface n’est influencée que par le
vent local, c’est à dire qu’il n’y a pas de houle. L’état de la surface océanique est modélisé
par le spectre de mer du vent décrit dans la section 4.3.4, c’est-à-dire le modèle DV2. La
valeur du CDN est dérivé de (4.75) et (4.77) avec z0 derivé du modèle Pierson76 donné par
(4.83). Le modèle KS est utilisé pour la constante diélectrique. L’écume n’est pas prise en
compte.
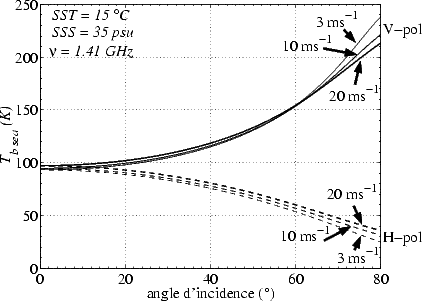
La figure 4.42 illustre la variation de Tbmer omnidirectionnelle, c’est à dire de Tbplat + Tb,0, en
fonction de  pour plusieurs vents et en polarisations verticale et horizontale. Les variations de T3,0 et
T4,0ne sont pas représentées car ces paramètres sont nuls sont nuls. L’angle d’incidence est limité à 80o
car pour les grands angles d’incidence, certains phénomènes physiques non pris en compte par le modèle,
comme les réflexions multiples, ont sûrement une influence sensible. Les résultats pour les grands angles
d’incidence sont donc à prendre avec précaution.
pour plusieurs vents et en polarisations verticale et horizontale. Les variations de T3,0 et
T4,0ne sont pas représentées car ces paramètres sont nuls sont nuls. L’angle d’incidence est limité à 80o
car pour les grands angles d’incidence, certains phénomènes physiques non pris en compte par le modèle,
comme les réflexions multiples, ont sûrement une influence sensible. Les résultats pour les grands angles
d’incidence sont donc à prendre avec précaution.
L’effet du vent sur Tbmer, et la variation de cet effet avec  sont très différents d’une polarisation à
l’autre. Une augmentation du vent diminue la variation de Tv mer avec theta et augmente celle de Thmer.
En effet, au nadir, l’effet du vent est le même sur les deux polarisations: quand le vent augmente, Tbmer
augmente. Lorsque
sont très différents d’une polarisation à
l’autre. Une augmentation du vent diminue la variation de Tv mer avec theta et augmente celle de Thmer.
En effet, au nadir, l’effet du vent est le même sur les deux polarisations: quand le vent augmente, Tbmer
augmente. Lorsque  augmente, l’effet du vent sur Tv mer diminue jusqu’à être nul à un angle d’incidence
variant entre 50o et 60o selon le vent. Pour des angles d’incidence supérieurs à 60o, l’effet du vent sur
la V-pol s’inverse et une augmentation du vent fait diminuer Tv mer. Pour la polarisation
horizontale au contraire, l’effet du vent est toujours d’augmenter Tbmer, et l’effet du vent augmente
quand
augmente, l’effet du vent sur Tv mer diminue jusqu’à être nul à un angle d’incidence
variant entre 50o et 60o selon le vent. Pour des angles d’incidence supérieurs à 60o, l’effet du vent sur
la V-pol s’inverse et une augmentation du vent fait diminuer Tv mer. Pour la polarisation
horizontale au contraire, l’effet du vent est toujours d’augmenter Tbmer, et l’effet du vent augmente
quand  augmente. Pour comprendre pourquoi l’influence du vent sur Tbmer est polarisée,
je vais dissocier les effets respectifs des rugosités de grande et de petite échelle en utilisant
respectivement un modèle dit ”grande échelle” (GE) et un modèle dit ”petite échelle” (PE). Une étude
sur l’effet relatif des petites et grandes échelles est reportée aussi dans l’annexe P, section
1.
augmente. Pour comprendre pourquoi l’influence du vent sur Tbmer est polarisée,
je vais dissocier les effets respectifs des rugosités de grande et de petite échelle en utilisant
respectivement un modèle dit ”grande échelle” (GE) et un modèle dit ”petite échelle” (PE). Une étude
sur l’effet relatif des petites et grandes échelles est reportée aussi dans l’annexe P, section
1.
Pour isoler l’effet des petites vagues, on suppose qu’il n’y a pas de grandes vagues et que la surface
océanique n’est recouverte que de rugosité de petite échelle (PE), dont la réflectivité RPE est donnée par
(4.103). Par conséquent, ces petites rugosités sont situées sur une surface horizontale dans le repère
terrestre et la modulation (4.94) induite par l’inclinaison de la surface des grandes vagues n’a pas lieu
d’être.
On a alors
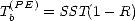
avec
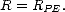
Pour isoler l’effet des grandes vagues, on suppose qu’il n’y a pas de rugosité de petite échelle. Par
conséquent, la surface des grandes vagues est lisse et leur réflectivité est calculée avec les coefficients de
Fresnel (R Fr ), qui sont intégrés sur la distribution statistique des pentes (i.e. intégrale pondérée par la
FDP sur les pentes), comme pour un modèle d’optique géométrique (OG). Les coefficients RFr sont
donnés en (2.23). Cependant, le modèle (GE) se distingue d’un modèle d’OG classique tel que celui
décri dans [73 ] ou dans [102] par la valeur de la variance de pentes utilisée dans la FDP.
Dans les modèles d’OG, la variance des pentes est couramment déduite du modèle empirique
de Cox et Munk ([14]), qui représente théoriquement la variance des pentes de toutes les
échelles de vagues (i.e. intégrée sur tout le spectre). Elle peut aussi être calculée à partir d’un
modèle de spectre. Dans le modèle GE, la variance des pentes est, comme dans le modèle deux
échelles, celle des grandes vagues uniquement car on se limite aux échelles de vagues pour
lesquelles l’approximation du plan tangent est valide (voir section 4.4). La variance des pentes du
modèle GE est donc plus faible que celle prédite par le modèle de Cox et Munk (voir section
4.4) , tant que le spectre est normalisé sur ces variances en tout cas. Elle est en tout cas
plus faible que celle calculée par intégration sur toutes les longueurs d’onde du spectre. Par
conséquent, l’effet des grandes vagues est plus faible avec un modèle GE qu’avec un modèle
d’OG.
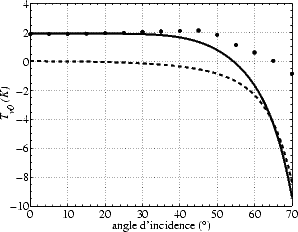
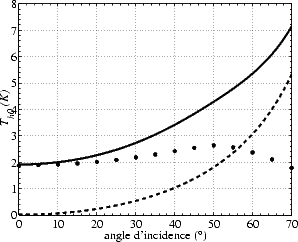
L’effet d’un vent de 8 m.s-1 sur les harmoniques 0, 1 et 2 de Tbmer est reporté sur les figures 4.43,
4.44 et 4.45 en fonction de l’angle d’incidence.
Au nadir, comme montré précédemment, Tb,0 est identique en V- et H-pol. Il vaut 2 K pour un vent
de 8 m.s-1 et il est induit par les petites échelles uniquement, car le modèle GE ne prédit pas d’effet du
vent sensible sur Tbmer en bande L et à cet angle d’incidence. Pourtant, des observations radiométriques à
basse fréquence, par Hollinger ([39]) à 1.41 GHz et par Blume et al. ([5]) à 2.65 GHz, ont mis en évidence
un effet du vent sur Tbmer à faible  , du même ordre de grandeur que celui prédit par le modèle deux
échelles (en l’occurrence par le modèle PE puisque la partie GE ne prédit aucun effet du vent). On
peut noter que Wilheit ([97]) aussi a mis en évidence une sensibilité au vent pour Tbmer en
bande L et au nadir ; mais il a attribué cet effet, probablement à tort, uniquement à l’influence
de l’écume (voir section 4.6.3). La modélisation de la diffusion de Bragg (i.e. diffusion par
les petites échelles) apparaît donc primordiale pour prendre en compte l’effet du vent sur
Tbmer.
, du même ordre de grandeur que celui prédit par le modèle deux
échelles (en l’occurrence par le modèle PE puisque la partie GE ne prédit aucun effet du vent). On
peut noter que Wilheit ([97]) aussi a mis en évidence une sensibilité au vent pour Tbmer en
bande L et au nadir ; mais il a attribué cet effet, probablement à tort, uniquement à l’influence
de l’écume (voir section 4.6.3). La modélisation de la diffusion de Bragg (i.e. diffusion par
les petites échelles) apparaît donc primordiale pour prendre en compte l’effet du vent sur
Tbmer.
Lorsque  augmente, Tv,0 varie très peu jusqu’à
augmente, Tv,0 varie très peu jusqu’à  = 40o, puis diminue rapidement jusqu’à être nul
vers
= 40o, puis diminue rapidement jusqu’à être nul
vers  = 55o (cet angle varie en fonction du vent) puis devient très négatif à 70o. Au contraire de Tv,0,
Th,0augmente quand
= 55o (cet angle varie en fonction du vent) puis devient très négatif à 70o. Au contraire de Tv,0,
Th,0augmente quand  augmente, et ce même aux faibles
augmente, et ce même aux faibles  : à
: à  = 70o, Th,0 vaut plus du triple de sa
valeur au nadir. Cette variation de l’effet du vent avec
= 70o, Th,0 vaut plus du triple de sa
valeur au nadir. Cette variation de l’effet du vent avec  est due un peu à la variation de l’effet des PE
avec
est due un peu à la variation de l’effet des PE
avec  , mais surtout à la variation de l’effet des grandes vagues avec
, mais surtout à la variation de l’effet des grandes vagues avec  , cet effet étant d’autant plus
sensible que
, cet effet étant d’autant plus
sensible que  est grand.
est grand.
L’effet des PE est toujours d’augmenter Tbmer, quels que soient  et la polarisation (sauf pour les très
grandes incidences, i.e.
et la polarisation (sauf pour les très
grandes incidences, i.e.  = 70o, et en V-pol où il fait légèrement diminuer Tbmer). Au contraire de l’effet
des PE, celui des GE est très polarisé : il fait augmenter Thmer et diminuer Tv mer à tous les
angles d’incidence. Par conséquent, les effets des deux échelles se renforcent en H-pol et se
contrarient en V-pol. La H-pol est donc d’autant plus sensible au vent que
= 70o, et en V-pol où il fait légèrement diminuer Tbmer). Au contraire de l’effet
des PE, celui des GE est très polarisé : il fait augmenter Thmer et diminuer Tv mer à tous les
angles d’incidence. Par conséquent, les effets des deux échelles se renforcent en H-pol et se
contrarient en V-pol. La H-pol est donc d’autant plus sensible au vent que  est grand car, quand
est grand car, quand  augmente, l’effet des GE augmente et l’effet des PE augmente (jusqu’à
augmente, l’effet des GE augmente et l’effet des PE augmente (jusqu’à  = 50o) ou diminue
moins vite que l’autre effet n’augmente (à partir de
= 50o) ou diminue
moins vite que l’autre effet n’augmente (à partir de  = 50o). En V-pol, quand
= 50o). En V-pol, quand  augmente
jusqu’à environ 40o, la faible variation des effets de PE et GE se compense et l’effet total reste
constant. Par contre, au délà de
augmente
jusqu’à environ 40o, la faible variation des effets de PE et GE se compense et l’effet total reste
constant. Par contre, au délà de  = 40o, l’effet des GE devient de plus en plus important à
mesure que
= 40o, l’effet des GE devient de plus en plus important à
mesure que  augmente, et devient prépondérant vers 60o. L’angle d’incidence pour lequel
Tv merest insensible au vent est donc celui où les effets des GE et des PE se compensent
exactement.
augmente, et devient prépondérant vers 60o. L’angle d’incidence pour lequel
Tv merest insensible au vent est donc celui où les effets des GE et des PE se compensent
exactement.
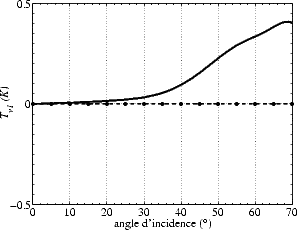
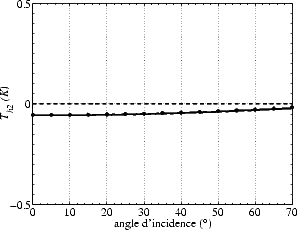
L’asymétrie upwind/downwind de Tbmer (i.e. Tb,1, figures 4.44 (a, c) et 4.45 (a, c)) au nadir est nulle ;
aux angles d’incidence inférieurs à 40o, elle est au maximum de ± 0.1 K pour un vent de 8 m.s-1. Aux
angles d’incidence plus élevés elle peut atteindre 0.4 K.
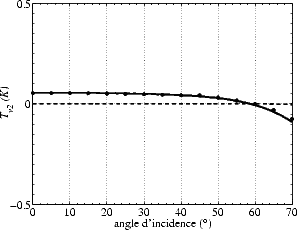
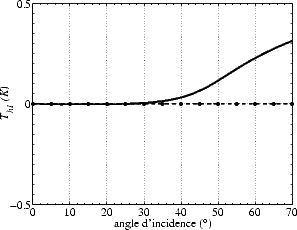
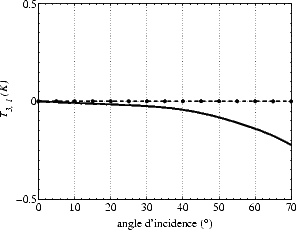
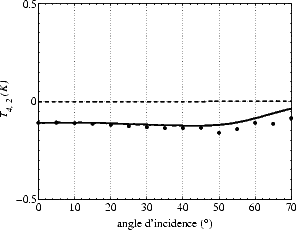
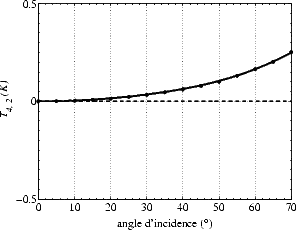
L’amplitude de la seconde harmonique (figures 4.44 (b, d) et 4.45 (b, d)) n’est pas nulle au nadir en V-
et H-pol. À U = 8 m.s-1, elle est de l’ordre de 0.05 K en V- et H-pol et est de signe opposé entre les deux
polarisations. Bien que les termes ”verticale” et ”horizontale” n’aient plus de sens au nadir, on a quand
même une T bmer polarisée (assez faiblement en bande L, contrairement aux plus hautes fréquences). Tb,2
est beaucoup plus faible en bande L qu’à plus haute fréquence, où elle est de l’ordre de 0.8 K à 19 GHz ou
37 GHz, soit un rapport de l’ordre de 16. La deuxième harmonique du spectre est déterminée par le
produit de l’harmonique 0 et de la fonction  (k) (voir la section 4.3.4). Alors que le spectre de
courbure n’est plus faible que d’un facteur 2 entre
(k) (voir la section 4.3.4). Alors que le spectre de
courbure n’est plus faible que d’un facteur 2 entre  = 21 cm et
= 21 cm et  de l’ordre du centimètre, la
fonction
de l’ordre du centimètre, la
fonction  (k) est plus faible d’un facteur 8. L’amplitude de Tb,2 est inférieure à 0.1 K en V- et
H-pol à tous les
(k) est plus faible d’un facteur 8. L’amplitude de Tb,2 est inférieure à 0.1 K en V- et
H-pol à tous les  , T3,2 vaut le double de Tv,2 et Th,2 et T3,2 est inférieur à 0.08 K pour
, T3,2 vaut le double de Tv,2 et Th,2 et T3,2 est inférieur à 0.08 K pour  inférieur à 40o et est de l’ordre de 0.25 K à 70o. Cependant, il faut noter que l’amplitude de
l’harmonique 2 dépend fortement du modèle de spectre (surtout de la fonction d’étalement)
et peut être sensiblement plus forte si elle est calculée avec le modèle de spectre ELF (voir
5.1.3).
inférieur à 40o et est de l’ordre de 0.25 K à 70o. Cependant, il faut noter que l’amplitude de
l’harmonique 2 dépend fortement du modèle de spectre (surtout de la fonction d’étalement)
et peut être sensiblement plus forte si elle est calculée avec le modèle de spectre ELF (voir
5.1.3).
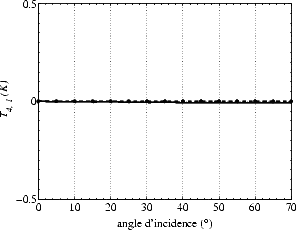
Le modèle GE ne prédit pour Tbmer aucune variation azimutale sensible. Là encore, la
prise en compte de la diffusion de Bragg est primordiale pour modéliser tous les effets du
vent. Concernant la seconde harmonique, l’absence d’effet de GE est dû au fait que, d’une
part, les coefficients de Fresnel sont isotropes, et, d’autre part, que la variance des pentes des
grandes échelles calculée avec le modèle DV2 est relativement isotrope (voir la figure 4.21).
Par conséquent, Tb,2 est essentiellement due aux petites échelles. Cependant, la première
harmonique étant due à un couplage des GE et des PE, ni le modèle GE, ni le modèle PE ne la
simulent.
On peut comparer ces résultats à ceux obtenu aux plus hautes fréquences auxquelles sont couramment
utilisés les modèles d’émissivité. L’effet omnidirectionnel du vent plus faible en bande L qu’à
plus haute fréquence, car l’amplitude du spectre de courbure autour de 21 cm est plus faible
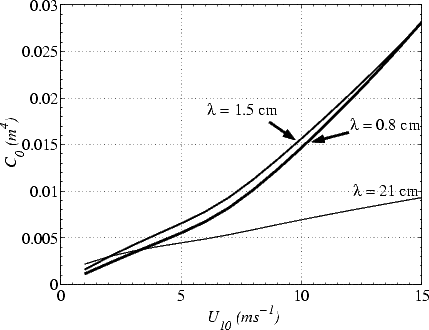
qu’à des longueurs d’onde plus courtes. J’ai représenté sur la figure 4.46 l’amplitude de la
composante omnidirectionnelle du spectre de courbure en fonction du vent aux longueurs
d’onde 21 cm, 1.5 cm et 0.8 cm qui correspondent respectivement aux fréquences 1.41 GHz,
19.65 GHz et 37 GHz. À 8 m.s-1, l’amplitude du spectre est sensiblement la même pour les
fréquences 19.65 GHz et 37 GHz, alors qu’à 1.41 GHz elle est deux fois plus faible que pour les
fréquences précédentes. La valeur de Tb,0 simulée aux différentes fréquences varie dans les mêmes
proportions. D’après Prigent et Abba ([73]), l’effet du vent au nadir simulé à haute fréquence (i.e.
à 89 GHz et 157 GHz) avec un modèle d’OG est loin d’être nul (fig 3 et 4 de l’article de
Prigent et Abba) ; en fait, cette influence du vent est dû essentiellement à la contribution
atmosphérique (l’effet n’est pas trivial, voir la section 6.3.2), comme le confirment les figures 6
et 7 de l’article de Prigent et Abba, sur lesquelles l’émissivité de l’océan est pratiquement
insensible au vent à faible  . L’amplitude de la première harmonique en bande L est faible, plus
faible qu’à haute fréquence car la variance des pentes des GE est plus faible et l’effet des PE
aussi. La variation azimutale de Tbmer en bande L est très faible, contrairement à celle à plus
haute fréquence (19.35 GHz et 37 GHz) où l’amplitude de la deuxième harmonique de Tbmer
pour un vent de 10 m.s-1 est de l’ordre de 1 K et où l’amplitude de la première harmonique
est de l’ordre de 0.8 K pour des angles d’incidence proche de 50o ([102]). Cette variabilité
azimutale à haute fréquence permet d’ailleurs d’estimer la direction du vent par radiométrie
polarimétrique.
. L’amplitude de la première harmonique en bande L est faible, plus
faible qu’à haute fréquence car la variance des pentes des GE est plus faible et l’effet des PE
aussi. La variation azimutale de Tbmer en bande L est très faible, contrairement à celle à plus
haute fréquence (19.35 GHz et 37 GHz) où l’amplitude de la deuxième harmonique de Tbmer
pour un vent de 10 m.s-1 est de l’ordre de 1 K et où l’amplitude de la première harmonique
est de l’ordre de 0.8 K pour des angles d’incidence proche de 50o ([102]). Cette variabilité
azimutale à haute fréquence permet d’ailleurs d’estimer la direction du vent par radiométrie
polarimétrique.
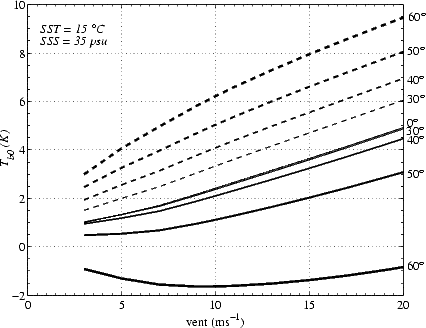
L’effet prépondérant du vent sur Tbmer en bande L porte sur la composante omnidirectionnelle. J’ai
reporté sur la figure 4.47 la variation de Tb,0 en fonction du vent, pour les polarisations verticale et
horizontale, à différents angles d’incidence. L’effet du vent sur Tb,0 est quasiment linéaire pour  inférieur
à 50o , excepté pour les vents très faibles, pour lesquels la variation de Tb,0 avec le vent est la plus rapide.
On peut ainsi dériver l’ordre de grandeur de la sensibilité de Tbmer au vent en calculant la pente de Tbmer
en fonction du vent entre 10 m.s-1 et 20 m.s-1. Cependant, les courbes ne sont pas rigoureusement
linéaires : on peut remarquer qu’il y a deux régimes de variation, selon que U soit inférieur ou
supérieur à environ 7 m.s-1. Au nadir, l’effet du vent est d’augmenter la Tbmer d’environ 0.25
K.m.s-1 . En V-pol, cet effet du vent reste relativement constant jusqu’à un angle d’incidence de
30o , et varie peu jusqu’à 40o. Au delà de
inférieur
à 50o , excepté pour les vents très faibles, pour lesquels la variation de Tb,0 avec le vent est la plus rapide.
On peut ainsi dériver l’ordre de grandeur de la sensibilité de Tbmer au vent en calculant la pente de Tbmer
en fonction du vent entre 10 m.s-1 et 20 m.s-1. Cependant, les courbes ne sont pas rigoureusement
linéaires : on peut remarquer qu’il y a deux régimes de variation, selon que U soit inférieur ou
supérieur à environ 7 m.s-1. Au nadir, l’effet du vent est d’augmenter la Tbmer d’environ 0.25
K.m.s-1 . En V-pol, cet effet du vent reste relativement constant jusqu’à un angle d’incidence de
30o , et varie peu jusqu’à 40o. Au delà de  = 40o, comme on l’a vu précédemment, lorsque
= 40o, comme on l’a vu précédemment, lorsque  augmente l’effet du vent diminue rapidement et devient nul puis négatif entre 50o et 60o. En
H-pol, l’effet du vent sur Tbmer augmente quand
augmente l’effet du vent diminue rapidement et devient nul puis négatif entre 50o et 60o. En
H-pol, l’effet du vent sur Tbmer augmente quand  augmente: il est de 0.28 K.m-1.s à 40o et
de 0.32 K.m-1 .s à 60o. Connaître le vent avec précision est donc très important, car une
variation de U de 1 m.s-1 a le même effet sur Tbmer qu’une variation de SSS de plusieurs
dizièmes de psu (voir de plus de 1 psu en H-pol, à grand angle d’incidence et dans les mers
froides).
augmente: il est de 0.28 K.m-1.s à 40o et
de 0.32 K.m-1 .s à 60o. Connaître le vent avec précision est donc très important, car une
variation de U de 1 m.s-1 a le même effet sur Tbmer qu’une variation de SSS de plusieurs
dizièmes de psu (voir de plus de 1 psu en H-pol, à grand angle d’incidence et dans les mers
froides).
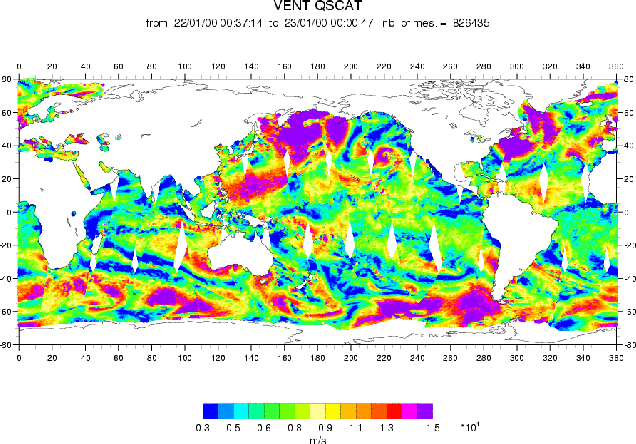
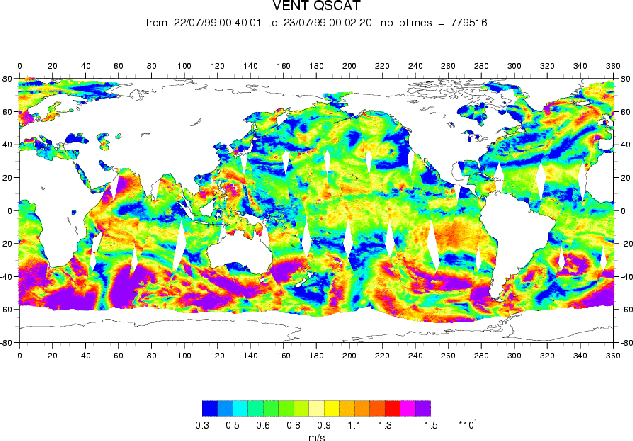
Pour illustrer l’ordre de grandeur des vents que rencontrera SMOS dans les différentes régions de
l’océan globale, deux cartes des vents mesurés par le diffusiomètre QSCAT à 25 km de résolution dans la
journée du 22 janvier 2000 (constituant un ensemble de plus de 826 000 mesures) et dans la journée du 22
juillet 1999 (constituant un ensemble de plus de 779 000 mesures) sont reportées respectivement sur les
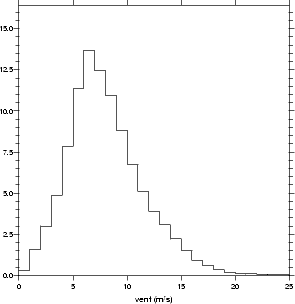
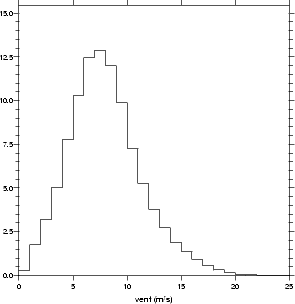
figures 4.48.a et 4.48.b. Les histogrammes correspondant sont reportés respectivement sur les figures
4.49.a et 4.49.b.
Le module du vent, estimé à une hauteur de dix mètres au dessus de la surface de l’océan (U10) à
partir de mesures QSCAT, est en moyenne globale d’environ 8 m.s-1. Son écart type est de 3.5 m.s-1. On
peut remarquer sur les cartes de la figure 4.48 que les grandes structures spatiales ont peu évolué entre
les différents passages orbitaux du satellite. Les vents sont toujours très forts dans l’océan
sud (i.e. au sud de 40oS), que ce soit en janvier ou en juillet (de l’ordre de 15 m.s-1). Ils
ont une forte variabilité saisonnière aux moyennes latitudes et en Atlantique et Pacifique
Nord.
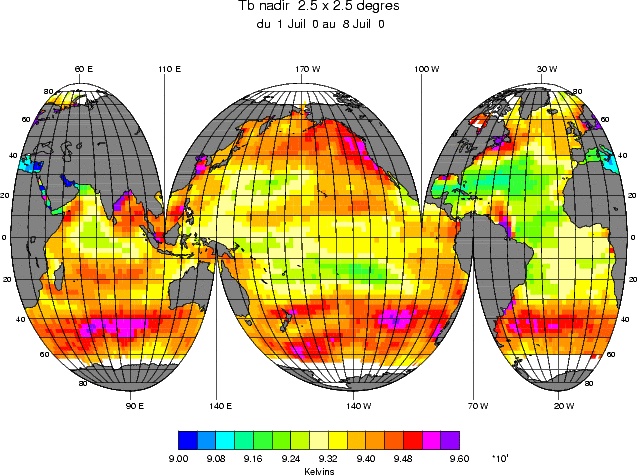
La T bmer au nadir en moyenne hebdomadaire, simulée à partir des SST et SSS climatologiques et des
vents instantannés dérivés des mesures QSCAT (voir la figure 4.38), est illustrée sur la figure 4.50. Sa
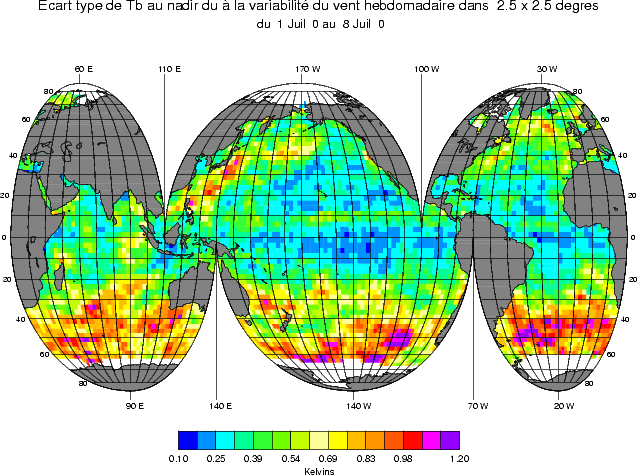
variabilité induite par la variabilité hebdomadaire du vent est illustrée sur la figure 4.51. La Tbmer est
supérieure de 2 K à la Tbplat en moyenne globale. Bien que le signal induit par le vent soit très fort,
particulièrement là où la variabilité spatiale du vent est forte et où celle de la SSS est faible, le signal
induit par la SSS est toujours visible dans certaines régions (par exemples aux embouchures des grands
fleuves et dans la zone des gyres subtropicaux). Les régions de fort vent, où la Tbmer est
fortement accrue, sont aussi parfois celles où la Tbplat est faible (à cause par exemple d’une forte
salinité dans la mer d’Arabie ou à cause de températures très faibles à 50oS). La prise en
compte du vent augmente la variabilité des Tbmer sur l’océan global: l’écart type des Tbmer
(moyennées sur 2.5o) montrées sur les figures 4.39 et 4.50 est respectivement de 0.76 K et de
0.90 K. On a donc une augmentation de la variabilité des Tbmer (moyennées sur 2.5o) de
20%.
La variabilité spatio-temporelle de Tbmer (figure 4.51) induite par la variabilité du vent pendant une
semaine et sur 2.5o est forte dans les zones de vent forts (de l’ordre de 1 K). Elles est plus faible (de
l’ordre de 0.2 K), en Atlantique et Pacifique tropical. Elle est néanmoins presque partout supérieure à 0.1
K, ce qui montre que la variabilité du vent à petites échelles de temps et d’espace induira une variabilité
sur les mesures de Tbmer non négligeable dans l’optique de l’estimation de la salinité. Il sera nécessaire
d’en tenir compte pour optimiser un éventuel étalonnage du radiomètre en vol (par vicarious
calibration).
 0 par rapport au vent, comme
cela a été fait pour le spectre de la mer du vent (section 4.3.4) et pour les coefficients de
diffusion (section 4.4). Pour les V- et H-pol, on ne conserve que les termes pairs car Tbvent est
symétrique par rapport à
0 par rapport au vent, comme
cela a été fait pour le spectre de la mer du vent (section 4.3.4) et pour les coefficients de
diffusion (section 4.4). Pour les V- et H-pol, on ne conserve que les termes pairs car Tbvent est
symétrique par rapport à 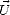 ([105]). On a ainsi respectivement en polarisations verticale et
horizontale
([105]). On a ainsi respectivement en polarisations verticale et
horizontale
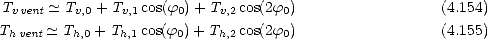
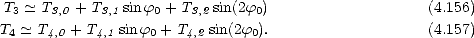

 . Long et Drinkwater ([
. Long et Drinkwater ([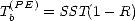
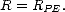
 (
(