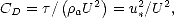
Dans les modèles de spectre de mer que j’ai utilisés ([30, 31]), la partie basse fréquence, c’est à dire celle qui correspond aux vagues de grande longueur d’onde, dépend du module du vent U, alors que la partie haute fréquence dépend de la vitesse de friction u* (voir (4.48)). Pour relier ces deux paramètres, on définit un coefficient de traînée (CD) qui traduit l’éfficacité du transfert de quantité de mouvement du vent vers la surface océanique ([80, 24, 44, 46]). On a alors
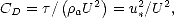 | (4.75) |
avec
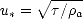 | (4.76) |
où  est la contrainte de cisaillement du vent et
est la contrainte de cisaillement du vent et 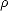 a est la densité de l’air. Le profil du vent est décrit
par une loi logarithmique de la forme
a est la densité de l’air. Le profil du vent est décrit
par une loi logarithmique de la forme
![[ ( ) ]
U(z) = u* ln z- - y (z)
k z0 M L](plan_html226x.gif) | (4.77) |
où  = 0.4 est la constante de Von Karman, z0 est longueur de rugosité aérodynamique, et
= 0.4 est la constante de Von Karman, z0 est longueur de rugosité aérodynamique, et 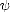 M est une
fonction qui traduit l’influence de la différence de température entre l’air et la mer (i.e. la stabilité) sur le
profil du vent, avec L, la longueur de stabilité Monin-Obukhov.
M est une
fonction qui traduit l’influence de la différence de température entre l’air et la mer (i.e. la stabilité) sur le
profil du vent, avec L, la longueur de stabilité Monin-Obukhov.
La longueur de stabilité L est une fonction de  T = TAir - TMer dont l’expression est donnée dans
[80 , 35 ]. Quand l’air au dessus de la surface de la mer est plus chaud que l’eau de mer, il se refroidit au
contact de la mer et la colonne d’air est stable. Quand l’air est plus froid que l’eau de mer, il se réchauffe
et par conséquence s’élève, créant ainsi des turbulences et rendant l’atmosphère instable. Ainsi,
T = TAir - TMer dont l’expression est donnée dans
[80 , 35 ]. Quand l’air au dessus de la surface de la mer est plus chaud que l’eau de mer, il se refroidit au
contact de la mer et la colonne d’air est stable. Quand l’air est plus froid que l’eau de mer, il se réchauffe
et par conséquence s’élève, créant ainsi des turbulences et rendant l’atmosphère instable. Ainsi,  T >
0o C caractérise essentiellement une atmosphère stable,
T >
0o C caractérise essentiellement une atmosphère stable,  T < 0oC une atmosphère instable et
T < 0oC une atmosphère instable et
 T = 0o C une atmosphère neutre. Il est à noter que que le profil d’humidité de l’air joue
aussi un rôle dans la stabilité. L’influence de la stabilité sur CD a notamment été étudiée
par Smith ([80 ]), Liu et Tang ([55]) et récemment par Guissard ([35]). Cette influence est
généralement faible. D’après [35], U10 dérivé d’un u* donné varie de l’ordre de ± 1 m.s-1
pour
T = 0o C une atmosphère neutre. Il est à noter que que le profil d’humidité de l’air joue
aussi un rôle dans la stabilité. L’influence de la stabilité sur CD a notamment été étudiée
par Smith ([80 ]), Liu et Tang ([55]) et récemment par Guissard ([35]). Cette influence est
généralement faible. D’après [35], U10 dérivé d’un u* donné varie de l’ordre de ± 1 m.s-1
pour  T = ±12o, cette variation étant un peu plus faible pour les atmosphères instables
(
T = ±12o, cette variation étant un peu plus faible pour les atmosphères instables
( T < 0) que pour les atmosphères stables (
T < 0) que pour les atmosphères stables ( T > 0). Cet ordre de grandeur est constant
pour tous les vents supérieurs à 5 m.s-1. De même, Liu et Tang ([55]) évaluent l’influence
de la stabilité à moins de 1 m.s-1 pour un
T > 0). Cet ordre de grandeur est constant
pour tous les vents supérieurs à 5 m.s-1. De même, Liu et Tang ([55]) évaluent l’influence
de la stabilité à moins de 1 m.s-1 pour un  T compris entre -5o et 3o. Nous avons testé
l’influence de la stabilité sur le profil du vent pour les vents mesurés durant la campagne
WISE 2001 à l’aide du modèle donné dans [55], et nous avons étudié l’influence de la stabilité
pendant cette campagne sur la dispersion des mesures de vent ; nous n’avons trouvé aucune
influence sensible (voir la section 7.3). De plus, comme SMOS ne disposera pas de la mesure
de
T compris entre -5o et 3o. Nous avons testé
l’influence de la stabilité sur le profil du vent pour les vents mesurés durant la campagne
WISE 2001 à l’aide du modèle donné dans [55], et nous avons étudié l’influence de la stabilité
pendant cette campagne sur la dispersion des mesures de vent ; nous n’avons trouvé aucune
influence sensible (voir la section 7.3). De plus, comme SMOS ne disposera pas de la mesure
de  T, je vais négliger l’influence de la stabilité sur le profil du vent. On déduit ainsi de
(4.75) et (4.77) le coefficient de trainée pour une atmosphère neutre (CDN) par la relation
suivante
T, je vais négliger l’influence de la stabilité sur le profil du vent. On déduit ainsi de
(4.75) et (4.77) le coefficient de trainée pour une atmosphère neutre (CDN) par la relation
suivante
![[ ]
---k--- 2
CDN = ln(z/z0) .](plan_html227x.gif) | (4.78) |
En utilisant le vent à 10 mètres de hauteur (U10), on définit
![[ ]
----k--- 2
C10N = ln(10/z0) .](plan_html228x.gif) | (4.79) |
Pour déterminer le profil du vent, on doit déterminer la longueur de rugosité aérodynamique z0. Une loi couramment utilisée est celle proposée par Smith ([80]), qui décompose z0 comme
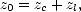 | (4.80) |
où zc , la rugosité aérodynamique proposé par Charnock ([12]), est induite par les petites vagues et dépend de u* . On a alors
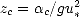 | (4.81) |
où g = 9.81 m.s-1 et  c vaut 0.011 ([80]) ou 0.012 ([13]) pour les mers pleinement developpées.
c vaut 0.011 ([80]) ou 0.012 ([13]) pour les mers pleinement developpées.  c est
plus grand dans les zones cotières ([34]), où la mer est partiellement développée (i.e. les vagues sont dites
jeunes ou matures) et où les pentes des petites vagues sont plus fortes. Je supposerai dans la suite que la
mer est pleinement développée car la majorité des mesures SMOS seront faites au large, mais le problème
de la proximité de la côte se posera pour l’utilisation de données acquises lors de campagnes de validation.
L’effet de la proximité de la côte sur l’état de mer, ainsi que sur la Tb induite, est étudié dans la section
5.1.5 en utilisant, entre autre, un modèle de z0 qui prend en compte le développement des vagues
([24 ]).
c est
plus grand dans les zones cotières ([34]), où la mer est partiellement développée (i.e. les vagues sont dites
jeunes ou matures) et où les pentes des petites vagues sont plus fortes. Je supposerai dans la suite que la
mer est pleinement développée car la majorité des mesures SMOS seront faites au large, mais le problème
de la proximité de la côte se posera pour l’utilisation de données acquises lors de campagnes de validation.
L’effet de la proximité de la côte sur l’état de mer, ainsi que sur la Tb induite, est étudié dans la section
5.1.5 en utilisant, entre autre, un modèle de z0 qui prend en compte le développement des vagues
([24 ]).
La longueur de rugosité pour une surface lisse zl dépend de la viscosité de l’air va et de la vitesse de friction u* comme
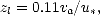 | (4.82) |
où va = 14 × 10-6 m.s-1 ([8]).
|
|
J’ai utilisé la longueur de rugosité proposée par Pierson ([71]), utilisée par Durden et Vesecky ([30]) et Yueh ([102 ]), et donnée par la relation suivante
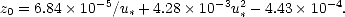 | (4.83) |
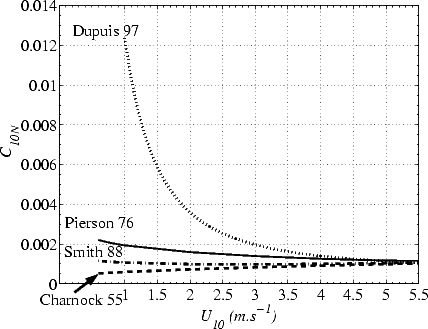
La figure 4.9 illustre le C10N dérivé des modèles de z0 de Charnock (Ch55), Smith (Sm88) et Pierson (Pi76). Les modèles Ch55 et Sm88 ne diffèrent que pour des vents inférieurs à 5 m.s-1 alors que le modèle Pi76 est systématiquement au dessus des deux autres. Il n’y a que pour des vents proches de 6 m.s -1 que le modèle Pi76 est en relativement bon accord avec les modèles Sm88 et Ch55 (voir les figures 4.10.a et 4.10.b). Pour un U10 fixé dans la gamme allant de 3 m.s-1 à 20 m.s-1, la vitesse de friction u* dérivée du modèle Pi76 diffère de 1% (à U10 = 6 m.s-1) à 20% de celle prédite par le modèle Sm88. La différence la plus forte entre les trois modèles est dans la gamme des vents faibles: à U10 = 1 m.s-1, le modèle Pi76 est trois fois plus fort en C10N que le modèle Ch55. Dupuis et al. ([27]) ont récemment (1997) étudié le C10N pour des vents inférieurs à 5.5 m.s-1 et proposé une loi reliant le C10N à U10. J’ai reporté sur la figure 4.11 les modèles Ch55, Sm88 et Pi76 à vents faibles, ainsi que celui proposé par Dupuis et al.. Ce dernier modèle est en bon accord avec les autres modèles pour U10 proche de 5 m.s-1, mais il diverge fortement pour les vents faibles, particulièrement pour U10 en dessous de 3 m.s-1. Par conséquent, le u* par vent faible pourrait être fortement sous-estimé par les modèles Ch55, Sm88 et même Pi76. Cependant, il faut noter qu’il est probable que pour des vents aussi faibles, les modèles de spectre de mer soient très incertains.
Les modèles de z0 que j’ai présentés jusqu’ici ne tiennent pas compte du développement partiel des vagues. En cas de fetch limité, il est nécessaire de prendre en compte d’autres paramètres que u*. Dans la section 5.1.5, j’ai utilisé la loi suivante proposée par Donelan et al. ([24 ])
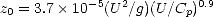 | (4.84) |
où z0 dépend de l’inverse de l’age de vagues 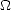 = U/Cp où U est le module du vent et Cp est la vitesse
de phase des vagues de longueur d’onde
= U/Cp où U est le module du vent et Cp est la vitesse
de phase des vagues de longueur d’onde  =
=  p, la longueur d’onde du pic basses fréquences du
spectre.
p, la longueur d’onde du pic basses fréquences du
spectre.
L’écart sur u* induit par les différences entre les z0 déduits de (4.83) (modèle Pierson) et de (4.80) (modèle Smith) peut atteindre un taux important de 20 % pour des vents de l’ordre de 3 m.s-1 ou 20 m.s-1. Le modèle de Smith est très couramment utilisé, mais le modèle de Pierson a été utilisé dans plusieurs modèles d’émissivité (modèle de Yueh, [102], modèle de l’Université Catholique de Louvain, [52]). Pour pouvoir effectuer des comparaisons cohérentes entre mes résultats et les résultats de ces modèles, notamment dans le cadre de l’étude [6], j’ai utilisé le modèle de Pierson. De plus, Durden et Vesecky, dont j’utilise le modèle de spectre des vagues, ont utilisé le modèle de Pierson pour établir leur modèle de spectre à partir de mesures diffusiométriques. L’amplitude du spectre des vagues est mal connue et elle est souvent ajustée sur des mesures radar ou radiométriques. On sait maintenant que le modèle de spectre DV (voir la section 7.3) induit une sous estimation de l’effet du vent sur la Tb. Utiliser le modèle de Smith reviendrait à diminuer l’effet du vent sur la Tb, ce qui serait contraire au observations.