J’ai reporté sur les figures 4.12, 4.13 et 4.14 les harmoniques 0 et 2 des spectres de puissance
et de courbure de la mer du vent calculées à partir du modèle de spectre DV2 (équations
4.48 et 4.52, avec la modification a0 = 0.008), du modèle de coefficient de traînée pour une
atmosphère neutre donné en (4.78) et du modèle de rugosité aérodynamique de Pierson (équation
4.83). Ces spectres sont représentés pour plusieurs vents couvrant la gamme des vents les
plus courants à la surface du globe (voir la section 4.6.2). J’ai mis en évidence la longueur
d’onde de 21 cm, car le rôle des vagues dont la taille est de cet ordre de grandeur est très
important dans le processus d’émissivité de la surface océanique en bande L (voir la section
4.4).
Le spectre omnidirectionnel de puissance est représenté sur la figure 4.12.a. Dans le domaine des
basses fréquences, on remarque la présence d’un pic dont la position et l’amplitude dépendent fortement
de U. Lorsque le vent augmente, le nombre d’onde du pic kp diminue et l’amplitude du spectre à ce
nombre d’onde augmente. L’amplitude de ces variations diminue à mesure que le vent augmente. Lorsque
U varie de 5 m.s-1 à 19 m.s-1, kp varie de 0.2 rad.m-1 à 0.015 rad.m-1, soit une variation de  p
de 30 m à 400 m. Dans le domaine des hautes fréquences, l’amplitude du spectre dépend
moins fortement de U. C’est notamment le cas pour les vagues dont la taille est proche de 21
cm.
p
de 30 m à 400 m. Dans le domaine des hautes fréquences, l’amplitude du spectre dépend
moins fortement de U. C’est notamment le cas pour les vagues dont la taille est proche de 21
cm.
En fait, comme on le verra dans la section 4.4, pour comprendre les variations d’émissivité avec le
vent, il est plus instructif d’étudier les variations du spectre de courbure dont la composante
omnidirectionnelle est représentée sur la figure 4.12.b. Le spectre de courbure présente un pic dans le
domaine des hautes fréquences, pour des longueurs d’onde de l’ordre de 2 cm (i.e. k = 300), dont
l’amplitude est très sensible à U (ou à u* en l’occurence). Ces longueurs d’ondes correspondent aux
vagues pour lesquelles le transfert d’énergie avec le vent se fait directement. On note qu’il existe pour ce
modèle de spectre une longueur d’onde insensible à U située à k = 2 rad.m-1, et que les petites vagues ne
décroissent pas rapidement pour les vents faibles. Par conséquent, lorsque U tend vers 0, l’énergie totale
du spectre ne tend pas vers 0 comme l’illustre la figure 4.13 où est représenté le spectre pour les vents
faibles.
La figure 4.14 illustre l’amplitude de la seconde harmonique des spectres de puissance (a) et de
courbure (b) de la mer du vent. Cette harmonique traduit la variation angulaire de l’énergie des vagues
due à l’asymétrie upwind/crosswind. Elle est obtenue, d’après (4.71) et (4.66), en multipliant 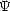 0 et C0
par
0 et C0
par  (k) qui est représenté sur la figure 4.15. D’après le modèle DV2, l’asymétrie upwind/crosswind ne
concerne que les petites vagues (k > 10,
(k) qui est représenté sur la figure 4.15. D’après le modèle DV2, l’asymétrie upwind/crosswind ne
concerne que les petites vagues (k > 10, < 60 cm) (voir les figures 4.14.b et 4.15). On verra dans la
section 5.1.3 que ce n’est pas le cas avec tous les modèles de spectre. La sensibilité de la seconde
harmonique au vent pour U compris entre 5 m.s-1 et 15 m.s-1 est similaire à celle de l’harmoniques 0 car
< 60 cm) (voir les figures 4.14.b et 4.15). On verra dans la
section 5.1.3 que ce n’est pas le cas avec tous les modèles de spectre. La sensibilité de la seconde
harmonique au vent pour U compris entre 5 m.s-1 et 15 m.s-1 est similaire à celle de l’harmoniques 0 car
 (k) est peu sensible à U dans cette gamme de vent. Pour les vagues dont la taille est de
l’ordre de 21 cm,
(k) est peu sensible à U dans cette gamme de vent. Pour les vagues dont la taille est de
l’ordre de 21 cm,  (k) est faible, beaucoup plus faible (d’un facteur 6) que pour les petites
vagues dont la taille est de l’ordre de quelques centimètres. On verra que cette différence
induit une variation azimutale de Tbmer beaucoup plus faible en bande L qu’à plus haute
fréquence.
(k) est faible, beaucoup plus faible (d’un facteur 6) que pour les petites
vagues dont la taille est de l’ordre de quelques centimètres. On verra que cette différence
induit une variation azimutale de Tbmer beaucoup plus faible en bande L qu’à plus haute
fréquence.
 p
de 30 m à 400 m. Dans le domaine des hautes fréquences, l’amplitude du spectre dépend
moins fortement de U. C’est notamment le cas pour les vagues dont la taille est proche de 21
cm.
p
de 30 m à 400 m. Dans le domaine des hautes fréquences, l’amplitude du spectre dépend
moins fortement de U. C’est notamment le cas pour les vagues dont la taille est proche de 21
cm.
 0 et C0
par
0 et C0
par  (k) qui est représenté sur la figure 4.15. D’après le modèle DV2, l’asymétrie upwind/crosswind ne
concerne que les petites vagues (k > 10,
(k) qui est représenté sur la figure 4.15. D’après le modèle DV2, l’asymétrie upwind/crosswind ne
concerne que les petites vagues (k > 10, < 60 cm) (voir les figures 4.14.b et 4.15). On verra dans la
section 5.1.3 que ce n’est pas le cas avec tous les modèles de spectre. La sensibilité de la seconde
harmonique au vent pour U compris entre 5 m.s-1 et 15 m.s-1 est similaire à celle de l’harmoniques 0 car
< 60 cm) (voir les figures 4.14.b et 4.15). On verra dans la
section 5.1.3 que ce n’est pas le cas avec tous les modèles de spectre. La sensibilité de la seconde
harmonique au vent pour U compris entre 5 m.s-1 et 15 m.s-1 est similaire à celle de l’harmoniques 0 car
 (k) est peu sensible à U dans cette gamme de vent. Pour les vagues dont la taille est de
l’ordre de 21 cm,
(k) est peu sensible à U dans cette gamme de vent. Pour les vagues dont la taille est de
l’ordre de 21 cm,  (k) est faible, beaucoup plus faible (d’un facteur 6) que pour les petites
vagues dont la taille est de l’ordre de quelques centimètres. On verra que cette différence
induit une variation azimutale de Tbmer beaucoup plus faible en bande L qu’à plus haute
fréquence.
(k) est faible, beaucoup plus faible (d’un facteur 6) que pour les petites
vagues dont la taille est de l’ordre de quelques centimètres. On verra que cette différence
induit une variation azimutale de Tbmer beaucoup plus faible en bande L qu’à plus haute
fréquence.