|
|
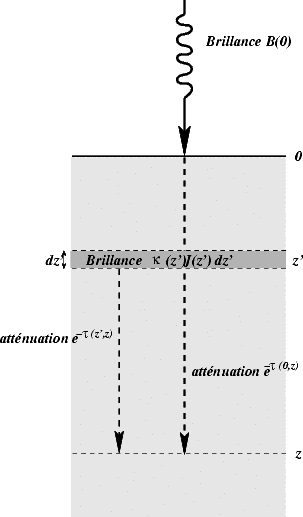
On suppose que l’on a une brillance 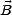 (0) qui arrive à la frontière d’un milieu (ici l’atmosphère) en se
propageant le long du vecteur
(0) qui arrive à la frontière d’un milieu (ici l’atmosphère) en se
propageant le long du vecteur 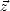 (voir figure 6.3). La diminution de brillance (l’extinction) le long d’un
trajet élémentaire dz au point z est donnée par
(voir figure 6.3). La diminution de brillance (l’extinction) le long d’un
trajet élémentaire dz au point z est donnée par
où  e (z) est le coefficient d’extinction du milieu (en nepers.m-1). L’extinction est due soit à de
l’absorption d’énergie par le milieu (l’énergie radiative est transformée en une autre forme d’énergie
comme de la chaleur par exemple) soit à de la diffusion (i.e. l’énergie est rayonnée dans d’autres directions
que
e (z) est le coefficient d’extinction du milieu (en nepers.m-1). L’extinction est due soit à de
l’absorption d’énergie par le milieu (l’énergie radiative est transformée en une autre forme d’énergie
comme de la chaleur par exemple) soit à de la diffusion (i.e. l’énergie est rayonnée dans d’autres directions
que 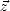 qui est la direction du rayonnement incident). Le coefficient d’extinction s’écrit alors
qui est la direction du rayonnement incident). Le coefficient d’extinction s’écrit alors
où  a (z) est le coefficient d’absorption et
a (z) est le coefficient d’absorption et  d(z) est le coefficient de diffusion.
d(z) est le coefficient de diffusion.
L’augmentation de brillance (par émission) le long d’un trajet élémentaire dz est donnée par
où Ja et Jd sont les fonctions source respectivement de l’émission thermique et de la diffusion. Sous la condition d’équilibre thermodynamique local, l’émission thermique et l’absorption étant égales, Ja est la fonction source d’absorption. En définissant l’albédo de diffusion ad comme
et en utilisant (6.4), (6.5) s’écrit sous la forme
où J(z) = [1 - ad(z)]Ja(z) + ad(z)Jd(z) est la fonction source effective totale.
Pour déterminer la variation totale de brillance dB(z) le long de dz, on somme l’extinction et l’émission, c’est à dire (6.3) et (6.7), et l’on obtient l’équation de transfert radiatif suivante
où d =
=  e dz est l’épaisseur optique d’une couche d’atmosphère d’épaisseur dz. La résolution de (6.9)
nous fournit les contributions de chaque couche atmosphérique élémentaire, que l’on va intégrer sur une
épaisseur donnée d’atmosphère. Je vais dans un premier temps déterminer la solution de l’équation de
transfert radiatif puis déterminer l’épaisseur d’atmosphère à considérer en fonction de l’angle
d’incidence.
e dz est l’épaisseur optique d’une couche d’atmosphère d’épaisseur dz. La résolution de (6.9)
nous fournit les contributions de chaque couche atmosphérique élémentaire, que l’on va intégrer sur une
épaisseur donnée d’atmosphère. Je vais dans un premier temps déterminer la solution de l’équation de
transfert radiatif puis déterminer l’épaisseur d’atmosphère à considérer en fonction de l’angle
d’incidence.