
 =
=  e(z)dz où
e(z)dz où  e(z) est le coefficient d’extinction de
l’atmosphère en z. Pour avoir l’épaisseur optique totale, on intègre d
e(z) est le coefficient d’extinction de
l’atmosphère en z. Pour avoir l’épaisseur optique totale, on intègre d sur le trajet parcouru par le
rayonnement. Pour un rayonnement se propageant le long du vecteur normal à la surface de
l’océan, on calcule l’épaisseur optique de l’atmosphère entre une altitude z1 et z2 comme étant
sur le trajet parcouru par le
rayonnement. Pour un rayonnement se propageant le long du vecteur normal à la surface de
l’océan, on calcule l’épaisseur optique de l’atmosphère entre une altitude z1 et z2 comme étant
Le cas d’un rayonnement en incidence oblique est traité dans la section 6.2.3. L’équation (6.9) peut se ramener ainsi ([90]) à la solution formelle
Pour des fréquences aussi basses que celles de la bande L, la diffusion atmosphérique est négligeable en
l’absence de pluie et l’on a essentiellement de l’extinction atmosphérique. Les constituants atmosphériques
susceptibles de diffuser le rayonnement sont les gouttes d’eau dont la taille peut varier de quelques 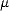 m à
quelques millimètres, la taille des molécules et atomes étant très négligeable devant la longueur
d’onde qui nous concerne (i.e. 21 cm). Dans les nuages non précipitants, les gouttes d’eau
ont des tailles de l’ordre de 10 à 200
m à
quelques millimètres, la taille des molécules et atomes étant très négligeable devant la longueur
d’onde qui nous concerne (i.e. 21 cm). Dans les nuages non précipitants, les gouttes d’eau
ont des tailles de l’ordre de 10 à 200 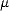 m, valeurs pour lesquelles la diffusion est négligeable
[90 ]. En cas de présence de pluie, la taille des gouttes d’eau peut atteindre le millimètre et la
diffusion du rayonnement par ces gouttes peut être à l’origine d’une modification sensible
(de l’ordre de quelques K) de la TA [79]. De plus, il est probable que l’impact de la pluie
modifie la rugosité de la surface océanique et modifie ainsi la température de brillance de
l’océan. Le cas de la pluie ne sera pas abordé dans cette thèse, où je me limiterai à l’étude de
l’influence de la vapeur d’eau atmosphérique non précipitante. Par conséquent, le terme de
diffusion est nul dans (6.4), (6.5) et (6.6) et la brillance ne dépend plus que du phénomène
d’absorption. Sous l’hypothèse d’équilibre thermodynamique local, on peut exprimer (6.11) sous la
forme
m, valeurs pour lesquelles la diffusion est négligeable
[90 ]. En cas de présence de pluie, la taille des gouttes d’eau peut atteindre le millimètre et la
diffusion du rayonnement par ces gouttes peut être à l’origine d’une modification sensible
(de l’ordre de quelques K) de la TA [79]. De plus, il est probable que l’impact de la pluie
modifie la rugosité de la surface océanique et modifie ainsi la température de brillance de
l’océan. Le cas de la pluie ne sera pas abordé dans cette thèse, où je me limiterai à l’étude de
l’influence de la vapeur d’eau atmosphérique non précipitante. Par conséquent, le terme de
diffusion est nul dans (6.4), (6.5) et (6.6) et la brillance ne dépend plus que du phénomène
d’absorption. Sous l’hypothèse d’équilibre thermodynamique local, on peut exprimer (6.11) sous la
forme
où T b (z) est la température de brillance en z, Tb(0) est la température de brillance à l’entrée de
l’atmosphère et T(z') est la température physique de la couche située en z' ([90]). Par conséquent,
la température de brillance Tb(z) en un point z est la somme de la brillance à l’entrée de
l’atmosphère T b (0) atténuée le long du trajet entre 0 et z (le facteur d’attenuation étant donné par
e- (0,z) ) et de la Tb'émise par le milieu (voir figure 6.3 qui illustre ce phénomène en terme de
brillance).
(0,z) ) et de la Tb'émise par le milieu (voir figure 6.3 qui illustre ce phénomène en terme de
brillance).
Cette T b ' émise par le milieu est la somme de la Tb émise par chacune des couches élémentaires du
milieu, atténuée sur la distance séparant la couche élémentaire de la couche située en z. La dTb'(z') d’une
couche élémentaire située en z' et d’épaisseur élémentaire dz' est donnée par  e(z')T(z')dz'.
L’atténuation de dTb'(z') entre z' et z est donnée par le facteur e-
e(z')T(z')dz'.
L’atténuation de dTb'(z') entre z' et z est donnée par le facteur e- (z',z).
(z',z).
Si  (z', z) est négligeable quel que soit z', l’atténuation n’a pas d’influence sur la température de
brillance en z et celle-ci est principalement influencée par les couches dont la température de brillance est
la plus forte (i.e. les couches où
(z', z) est négligeable quel que soit z', l’atténuation n’a pas d’influence sur la température de
brillance en z et celle-ci est principalement influencée par les couches dont la température de brillance est
la plus forte (i.e. les couches où  eT est le plus élevé), indépendemment de leur distance à z. Dans ce cas,
le milieu est dit transparent. On verra par la suite que l’atmosphère est transparente en bande
L.
eT est le plus élevé), indépendemment de leur distance à z. Dans ce cas,
le milieu est dit transparent. On verra par la suite que l’atmosphère est transparente en bande
L.