 (qui est l’angle d’incidence) par
rapport à la normale à la surface au point O (voir figure 6.4).
(qui est l’angle d’incidence) par
rapport à la normale à la surface au point O (voir figure 6.4).
Je vais déterminer l’épaisseur d’atmosphère traversée par un onde émise au point O situé sur la surface
terrestre et reçue au point M situé à l’altitude z et dans la direction  (qui est l’angle d’incidence) par
rapport à la normale à la surface au point O (voir figure 6.4).
(qui est l’angle d’incidence) par
rapport à la normale à la surface au point O (voir figure 6.4).
On pose R t 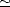 6370 km, le rayon terrestre,
6370 km, le rayon terrestre, 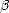 , l’angle au centre de la Terre entre le point O et le point
M et L l’épaisseur d’atmosphère recherchée.
, l’angle au centre de la Terre entre le point O et le point
M et L l’épaisseur d’atmosphère recherchée.
La figure 6.5 représente la géométrie du problème précédemment énoncé. On connait Rt, z,  ' =
' =  -
- .
On ne connait ni
.
On ne connait ni 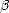 ni L que l’on cherche. Pour éliminer
ni L que l’on cherche. Pour éliminer 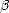 du problème, on va utiliser la règle des cosinus
qui nous dit que
du problème, on va utiliser la règle des cosinus
qui nous dit que
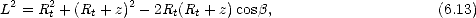
et la règle des sinus nous dit que

En écrivant que sin2 + cos2
+ cos2 = 1, il vient
= 1, il vient
On résoud numériquement 6.15 ou 6.16 au choix, selon que l’on veuille passer de l’épaisseur L à
l’altitude z ou vice versa. On obtient pour L(z, ) deux solutions positives (et deux solutions négatives car
le polynôme est d’ordre 4), dont une est rejetée car elle impose un rayon passant par l’intérieur de la
Terre (c’est la plus grande solution pour L).
) deux solutions positives (et deux solutions négatives car
le polynôme est d’ordre 4), dont une est rejetée car elle impose un rayon passant par l’intérieur de la
Terre (c’est la plus grande solution pour L).
La variation de l’épaisseur d’atmosphère traversée en fonction de l’altitude, pour plusieurs angles  est
illustrée sur la figure 6.6. Cette variation est toujours linéaire, sauf pour le cas extrême de l’incidence
rasante (i.e.
est
illustrée sur la figure 6.6. Cette variation est toujours linéaire, sauf pour le cas extrême de l’incidence
rasante (i.e.  = 90o). Plus l’angle d’incidence est élevé, plus l’épaisseur d’atmosphère traversée pour une
altitude donnée est grande. L’épaisseur atmosphérique traversée est, pour une atmosphère supposée
atteindre une altitude de l’ordre de 18 km, au plus de 100 km pour l’essentiel des angles d’incidence. Pour
le cas extrême
= 90o). Plus l’angle d’incidence est élevé, plus l’épaisseur d’atmosphère traversée pour une
altitude donnée est grande. L’épaisseur atmosphérique traversée est, pour une atmosphère supposée
atteindre une altitude de l’ordre de 18 km, au plus de 100 km pour l’essentiel des angles d’incidence. Pour
le cas extrême  = 90o, cette épaisseur peut atteindre 500 km. Ce cas nécessite que l’angle d’élévation soit
de l’ordre de 70o pour un satellite, et de plus de 80o pour un avion (voir l’annexe M). En
prenant en compte la largeur de lobe des différents instruments (environ 1o pour SMOS et 15o
pour le STARRS, voir la section 7.1.2.2), de telles élévations ont une contribution négligeable
dans le cas de SMOS, et ont rarement une contribution sensible dans le cas des campagnes
aéroportées.
= 90o, cette épaisseur peut atteindre 500 km. Ce cas nécessite que l’angle d’élévation soit
de l’ordre de 70o pour un satellite, et de plus de 80o pour un avion (voir l’annexe M). En
prenant en compte la largeur de lobe des différents instruments (environ 1o pour SMOS et 15o
pour le STARRS, voir la section 7.1.2.2), de telles élévations ont une contribution négligeable
dans le cas de SMOS, et ont rarement une contribution sensible dans le cas des campagnes
aéroportées.
Pour un radiomètre en visée oblique, on remplace dz' dans (6.10) et (6.12) par dL(z', ), l’épaisseur
d’atmosphère élémentaire à une altitude z et à une incidence
), l’épaisseur
d’atmosphère élémentaire à une altitude z et à une incidence  . On a ainsi, pour un theta donné, les
expression suivantes
. On a ainsi, pour un theta donné, les
expression suivantes
et
pour respectivement l’épaisseur optique et la température de brillance en incidence oblique.
Si l’atmosphère s’étend d’une altitude z0 = 0 à une altitude zlim, alors on définit l’épaisseur optique totale par l’expression suivante
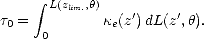 | (6.19) |