Les coordonnées locales sont attachées à la surface d’une vague de grande échelle. On définit l’axe
zénithal local d’une vague 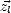 comme étant la normale à la surface de la vague (voir la figure 7.35). Je vais
déterminer l’expression des vecteurs
comme étant la normale à la surface de la vague (voir la figure 7.35). Je vais
déterminer l’expression des vecteurs 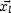 ,
, 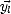 et
et 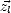 dans le repère terrestre (i.e. dans la base (
dans le repère terrestre (i.e. dans la base (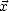 ,
, 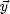 ,
,
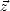 )).
)).
On représente la surface d’une vague qui a des pentes Sx = -Z/X et Sy = -Z/Y respectivement le
long de 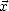 et de
et de 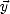 (voir la figure 7.36), par l’equation suivante
(voir la figure 7.36), par l’equation suivante
On déduit de (J.70) l’équation de la normale 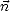 à la surface de la vague, qui est définie par
à la surface de la vague, qui est définie par 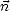 ||
||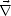 S
où
S
où
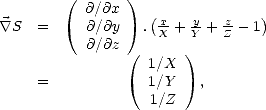
soit, d’après les définitions de Sx et de Sy
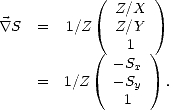
Le vecteur  étant normalisé, on a
étant normalisé, on a

où || S|| est la norme de
S|| est la norme de 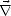 S donnée par
S donnée par

Il vient alors
Comme par définition 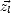 =
= 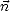 , on a aussi
, on a aussi
Il faut définir 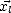 et
et 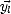 pour avoir une base locale (
pour avoir une base locale (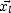 ,
, 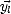 ,
, 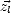 ) complète. Le vecteur
) complète. Le vecteur 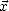 du repère terrestre
est définit comme étant dans la direction du vent. On définit alors
du repère terrestre
est définit comme étant dans la direction du vent. On définit alors 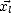 comme étant dans le plan formé par
les vecteurs
comme étant dans le plan formé par
les vecteurs 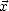 et -
et -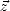 (et comme étant dans le plan de la vague), ce qui fait de
(et comme étant dans le plan de la vague), ce qui fait de 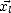 la direction de symétrie
des vagues de petite échelle superposées à la vague de grande échelle. On écrit ainsi
la direction de symétrie
des vagues de petite échelle superposées à la vague de grande échelle. On écrit ainsi 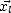 sous la
forme
sous la
forme
De plus, la base (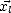 ,
, 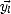 ,
, 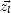 ) étant définie comme orthonormée, les relations suivantes doivent être
vérifiées
) étant définie comme orthonormée, les relations suivantes doivent être
vérifiées