Pour exprimer explicitement les vecteurs 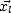 ,
, 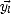 et
et 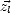 dans la base (
dans la base (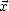 ,
, 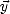 ,
, 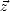 ) en fonction des pentes Sx et
Sy , je vais déterminer
) en fonction des pentes Sx et
Sy , je vais déterminer 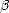 . On peut exprimer
. On peut exprimer 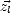 en fonction des angle
en fonction des angle  n et
n et  n (voir la figure 7.37)
comme
n (voir la figure 7.37)
comme
où  n est l’angle entre le zenith
n est l’angle entre le zenith 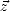 et le zenith local
et le zenith local 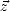 et
et  n est l’angle d’azimut de
n est l’angle d’azimut de 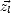 dans le repère
terrestre.
dans le repère
terrestre.
Pour déterminer  n et
n et  n, on identifit (J.74) et (J.77). Il vient
n, on identifit (J.74) et (J.77). Il vient
On déduit alors de (J.78) et (J.78)
avec  n inférieur à 90o (par conséquent l’argument de l’arcsin est positif et il n’y a pas de solution
négative quand on prend la racine). En utilisant (J.81), (J.82) et (J.79), il vient
n inférieur à 90o (par conséquent l’argument de l’arcsin est positif et il n’y a pas de solution
négative quand on prend la racine). En utilisant (J.81), (J.82) et (J.79), il vient
On a ainsi une expression explicite de  n et
n et  n en fonction des pentes Sx et Sy.
n en fonction des pentes Sx et Sy.
Je vais déterminer 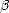 en fontion de
en fontion de  n et
n et  n, et donc en fonction de Sx et Sy, à l’aide de la deuxième
des relations (J.76). il vient alors
n, et donc en fonction de Sx et Sy, à l’aide de la deuxième
des relations (J.76). il vient alors
On a ainsi une expression de 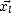 en fonction des pentes avec (J.75) et (J.86). On détermine
en fonction des pentes avec (J.75) et (J.86). On détermine 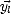 par la
première des relations (J.76) d’où il vient
par la
première des relations (J.76) d’où il vient
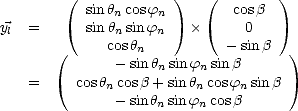
,
soit, en remplaçant 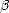 par son expression en fonction de
par son expression en fonction de  n et
n et  n donnée en (J.85),
n donnée en (J.85),