



Next: 2.2 Fondements mathématiques :
Up: 2. Principes fondamentaux de
Previous: 2. Principes fondamentaux de
Tout comme la radiométrie à puissance totale, la
radiométrie à synthèse d'ouverture trouve ses origines dans
l'observation astronomique, et plus particulièrement dans
l'application de l'interférométrie. Dès 1868,
le physicien français ARMAND-HIPPOLYTE LOUIS FIZEAU affirme :
Il existe en effet pour la plupart des phénomènes
d'interférence, [...] une relation remarquable et nécessaire
entre la dimension des franges et celle de la source
lumineuse, [...], d'où, pour le dire en passant, il peut
être permis d'espérer qu'[...] il deviendra possible
d'obtenir quelques données nouvelles sur les diamètre
angulaires des astresFizeau.
L'interférométrie permet de tirer des informations sur les
propriétés d'une source lumineuse en séparant en deux le
signal issu de cette source et en combinant ces signaux
secondaires afin de faire apparaître des franges
lumineuses. Ces franges apparaissent du fait
de la nature ondulatoire de la lumière. Une analogie
possible est de considérer la rencontre des vagues causées
par la chute de deux pierres dans un étang : lorsque deux
crêtes se rencontrent, leur hauteur s'additionne pour
former une vague deux fois plus haute et lorsque une crête
rencontre un creux, leur influence respective
s'annule. Ainsi, en interférométrie optique, sous certaines
conditions, on voit apparaître une succession de franges
lumineuses et sombres. Il a été démontré que le pouvoir
séparateur d'un système interférométrique, sa résolution
spatiale, est amélioré lorsque la distance entre les
sources secondaires est augmentée.
Il faudra attendre 1920 pour que le physicien américain
ALBERT ABRAHAM MICHELSON mesure pour la première fois le
diamètre d'une étoile hors du système solaire à l'aide de
l'interférométrie mais l'interférométrie optique se heurtera
encore longtemps à la trop grande précision instrumentale requise.
Le premier radio-interféromètre est constitué, en 1950, de
deux antennes fixes, et l'interféromètre de
Owen's Valley, Californie, construit en 1957 à partir d'un couple
d'antennes orientables, est à l'origine de la découverte des
quasars.
Depuis, les distances entre les antennes élémentaires n'ont
cessé de s'accroître. Citons l'interféromètre 1
mile (1964) qui utilisa la rotation de la Terre pour
réaliser pour la première fois une synthèse
d'ouverture et ainsi obtenir une image dont la précision
était celle d'un télescope 1.5 km de diamètre, le
Very Large Array (VLA, pour Très Grand Réseau,
fin des années 70) à Socorro, Nouveau Mexique composé de 27
antennes formant un Y et synthétisant une antenne d'un
diamètre de 36 km, et enfin le
Very Long Baseline Array (VLBA, pour Réseau à
Très Grande Ligne de Base, 1985), qui en combinant les signaux
issus de 10 radio télescopes situés entre Hawaï et les Îles
Vierges, synthétisa un radio télescope d'un diamètre égal à
celui de la Terre. Certains projets en cours prévoient même
d'utiliser des instruments embarqués à bord de satellites
pour simuler des antennes d'un diamètre égal à plusieurs
fois celui de la Terre.
Le principe de la synthèse d'ouverture est donc de combiner les
signaux issus d'au moins deux antennes observant la même
scène et dont on fait varier
l'espacement. L'instrument ainsi composé, appelé
interféromètre, ne fournit pas
directement une tension proportionnelle à la température de
brillance de la scène observée mais une mesure de la
cohérence spatiale de cette scène, à partir de laquelle
 est estimé dans un deuxième temps.
est estimé dans un deuxième temps.
Cette technique permet notamment de synthétiser une antenne
d'un diamètre égal à la plus grande distance séparant deux
antennes élémentaires du radiomètre à synthèse d'ouverture.
Résolution spatiale (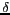 x [
x [
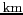 ]) pour un
radiomètre à synthèse d'ouverture)
La résolution spatiale d'un tel instrument, dont
l'espacement maximal entre deux antennes est noté
]) pour un
radiomètre à synthèse d'ouverture)
La résolution spatiale d'un tel instrument, dont
l'espacement maximal entre deux antennes est noté 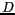 , est celle d'un
dispositif à antenne réelle doté d'une antenne de diamètre
, est celle d'un
dispositif à antenne réelle doté d'une antenne de diamètre 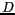 :
:
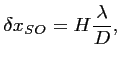 |
(2.1) |
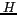 étant la distance entre l'instrument et la cible.
étant la distance entre l'instrument et la cible.
Les antennes doivent avoir un champ de vue se recouvrant
afin de pouvoir combiner leurs signaux. Elles doivent donc
posséder un lobe principal large c.-à-d. un diamètre 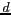 proche
de la longueur d'onde (
proche
de la longueur d'onde (
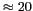 cm) :
cm) :
D'un point de vue pratique, il est plus facile de déployer
dans l'espace un ou plusieurs bras sur lesquels sont fixés des antennes de
petite dimension plutôt qu'une large parabole.
En faisant varier la distance entre deux antennes ou en
disposant un réseau d'antennes sur un plan (en formant par
exemple un Y, un U ou un T), la température de brillance
reconstruite sera une carte à 2 dimensions. Au cours du
survol d'un scène par un instrument, un même élément de
cette scène est vu successivement sous plusieurs angles
d'incidence : on retrouve là la capacité de mesure
multi-angulaire (pour la mesure de l'humidité) et les
mesures indépendantes au cours d'un même survol (mesure de
la salinité).
Il faut cependant noter que la distance 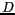 ne peut être
augmentée sans dégrader la sensibilité radiométrique.
Sensibilité radiométrique (
ne peut être
augmentée sans dégrader la sensibilité radiométrique.
Sensibilité radiométrique (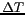 [K]) pour un radiomètre à
radiomètre à synthèse d'ouverture)
En synthèse d'ouverture PhilippeSensRad, la sensibilité radiométrique est
telle que :
[K]) pour un radiomètre à
radiomètre à synthèse d'ouverture)
En synthèse d'ouverture PhilippeSensRad, la sensibilité radiométrique est
telle que :
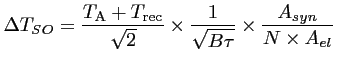 |
(2.4) |
où  est la surface de la parabole synthétisée, N
est le nombre d'antenne et
est la surface de la parabole synthétisée, N
est le nombre d'antenne et 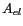 est la surface d'une
antenne élémentaire de diamètre
est la surface d'une
antenne élémentaire de diamètre 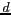 .
Pour
.
Pour 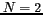 ,
,
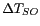 augmente alors avec le carré de la distance entre les
antennes :
augmente alors avec le carré de la distance entre les
antennes :
 |
(2.5) |
Cette relation ne fournit cependant qu'une valeur
approximative de la sensibilité radiométrique puisque
la mesure de  n'est pas directe et que l'imprécision sur
cette mesure dépend notamment des méthodes mises en oeuvre
pour estimer les températures de brillances à partir des
mesures instrumentales.
n'est pas directe et que l'imprécision sur
cette mesure dépend notamment des méthodes mises en oeuvre
pour estimer les températures de brillances à partir des
mesures instrumentales.
La mission spatiale SMOS (pour Soil Moisture and
Ocean Salinity , humidité des sols et salinité des
océans) représente la première tentative
d'application de la technique de synthèse d'ouverture à la
télédétection de la surface de la Terre. Ce projet, financé
par l'Agence Spatiale Européenne, a été initié en 1999 dans
le cadre du programme Exploration de la Terre
. Son objectif est de fournir, à la suite de son
lancement prévu en 2007, une mesure globale et
scientifiquement exploitable de l'humidité des continents
et de la salinité des océans. Il offre aussi l'occasion pour
la communauté scientifique de valider pour de futures
missions le concept prometteur d'imagerie par
interférométrie passive.
Cette mission regroupe une
centaine de chercheurs de divers pays européens (France, Espagne,
Allemagne, Finlande...) ainsi que quelques
chercheurs des Etats-Unis. Seuls une dizaine de chercheurs,
issus de l'Université Polytechnique de Catalogne (Espagne),
du Centre Allemand d'aéro- et astronautique (DLR, Allemagne),
et du Centre Européen de Recherche et de Formation en
Avancée en Calcul Scientifique (CERFACS, France), se consacrent
spécifiquement aux méthodes de reconstruction d'image.
L'instrument de mesure proprement dit, appelé MIRAS (Microwave Imaging
Radiometer with Aperture Synthesis), en cours de construction, sera composé
de 69 antennes régulièrement réparties sur 3 bras formant un
réseau en Y (voir Fig. 2.1). Il sera installé
sur une plateforme placée sur une orbite polaire à environ 755 km
d'altitude, avec un temps de revisite de l'ordre de 3 jours. Afin de valider
expérimentalement le principe de mesure, l'Université Technologique
de Helsinky (HUT, Finlande) a construit le HUT-2D, un réseau en U composé
de 36 antennes et prévu pour des missions aéroportées (voir Fig.
2.2). Le tableau 2.1 rappelle les
caractéristiques principales de ces deux instruments.
Quelque soit la géométrie, en U ou en Y, le fonctionnement est le même
: la corrélation des signaux issus de chaque couple
d'antennes fournira une mesure
instrumentale du degré de cohérence spatiale de la scène
observée. La reconstruction d'image pour les radiomètres
imageurs à synthèse d'ouverture consiste en un ensemble
cohérent d'outils mathématiques adaptés à la géométrie du
réseau et permettant au final une estimation de la carte à
deux dimensions de la distribution de températures de
brillance à partir des mesures interférométriques délivrées
par l'instrument. Ses objectifs se placent autant au niveau
d'une définition rigoureuse des espaces de travail (réseaux
hexagonaux ou cartésiens, directs ou réciproques), d'une
élaboration et d'une caractérisation d'outils adaptés à ces
espaces (fenêtres d'apodisation à deux dimensions,
optimisation de la forme de ces fenêtres, facteurs
de mérites spécifiques...) [PARTIE II] que dans le développement et
l'analyse de méthodes d'inversion robustes, rapides et
adaptées aux spécificités instrumentales [PARTIE III].
Les sections suivantes abordent les principes mathématiques et physiques
fondamentaux permettant d'introduire les concepts qui seront développés
dans la partie II.
Table 2.1: Caractéristiques de la mission spatiale SMOS
et de l'instrument HUT-2D.
| |
MIRAS
|
HUT-2D |
|
Configuration |
Y
|
U |
|
Type de mission |
spatiale / orbite polaire héliosynchrone
|
aéroportée |
|
Période d'activité |
courant 2007
2012
|
en cours |
|
Altitude |
755 km
|
3 km |
|
Orientation Inclinaison |
|
![\includegraphics[width=0.35\textwidth]{TiltETrotHUT2D.eps}](img185.gif) |
|
Nombre d'antennes |
(21 avants + 2 arrières )x3 = 69
|
12x3 = 36 |
|
Espacement inter-antennes |
0.875 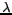
|
0.7 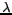
|
|
Dimension des bras |
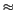
3.90 m
|
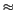 1.8 m
1.8 m |
|
Plus grande distance entre deux antennes |
6.70 m
|
 2.70 m
2.70 m |
|
Champ de vue |
|
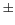 30
30
|
|
Résolution spatiale |
30 km < 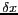
< 100 km
|
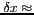 300 m
300 m |
Erreur attendue sur la  reconstruite
reconstruite |
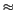
1 K
|
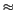 1 K
1 K |
|
Largeur à -3 dB du lobe principal (nominal) |
66 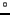
|
66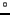
|
|
Fréquence centrale (nominale) |
1.4135 GHz
|
1.4135 GHz |
Longueur d'onde (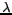 )(nominale)
)(nominale) |
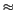
21.21 cm
|
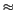 21.21 cm
21.21 cm |
|
Bande Passante (nominale) |
20 MHz
|
8 MHz |
|
Temps d'intégration |
1.5 s
|
1.5 s |
|
Nombre de visibilités complexes mesurées |
4692
|
1260 |
Nombre de pixels de la carte de  reconstruite
reconstruite |
128x128 = 16384
|
64x64 = 4096 |
|
Figure 2.1: Vue d'artiste du satellite SMOS : 69 antennes
sont régulièrement réparties sur les 3 bras en Y.
|
|
Figure 2.2: Schéma du dispositif instrumental du HUT-2D
: chacune des antennes disposées en U est reliée aux autres via
le corrélateur (ici au centre).
|
|




Next: 2.2 Fondements mathématiques :
Up: 2. Principes fondamentaux de
Previous: 2. Principes fondamentaux de
nous
2005-03-31
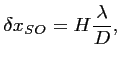
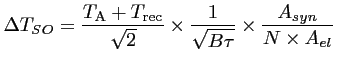

![\includegraphics[width=0.7\textwidth]{SMOSNB.eps}](img186.gif)
![\includegraphics[width=0.65\textwidth]{HUTNB.eps}](img187.gif)