Le champ incident sur le réseau interférométrique est polarisé et il est important d'avoir accès à la polarisation des températures de brillances observées pour augmenter la quantité d'information disponible pour l'estimation des paramètres géophysique.
Il a été précisé que les antennes d'un radiomètre à synthèse
d'ouverture sont équipés de deux ports orthogonaux, ![]() et
et
![]() . Or, le diagramme d'une antenne change selon que
le port
. Or, le diagramme d'une antenne change selon que
le port ![]() ou
ou ![]() est activé.
est activé.
Rappelons que les caractéristiques de polarisation d'un
champ électromagnétique sont parfaitement décrites par les valeurs des quatre
paramètres de STOKES
. Les composantes de STOKES de
![]() dans le repère de l'antenne sont alors notées
, avec :
dans le repère de l'antenne sont alors notées
, avec :
| (13.1) | |||
| (13.2) | |||
| (13.3) | |||
| (13.4) |
Les gains
co-polaires désignent les gains d'antennes du port ![]() ou
ou
![]() pour une onde incidente polarisée dans le même sens que
le port considéré. Les gains cross-polaires, d'un ordre de grandeur
plus faibles que les précédents, expriment une contamination du
diagramme par le couplage entre les polarisations. La valeur
des gains cross-polaires dépend de la qualité des antennes
pour une onde incidente polarisée dans le même sens que
le port considéré. Les gains cross-polaires, d'un ordre de grandeur
plus faibles que les précédents, expriment une contamination du
diagramme par le couplage entre les polarisations. La valeur
des gains cross-polaires dépend de la qualité des antennes
Les quatre composantes de STOKES sont explorées lors de séquences
durant lesquelles les ports des antennes d'un même couple
sont activés alternativement. Ce n'est donc plus 1 jeu de
visibilités mais 4 jeux de visibilités qui sont fournis à
chaque mesure instrumentale :
| (13.5) | |||
| (13.6) | |||
| (13.7) | |||
| (13.8) |
La relation de VAN CITTERT-ZERNIKE est alors considérablement complexifiée PWGCpolar:
e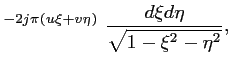 |
(13.9) |