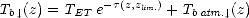
À la limite supérieure de la basse atmosphère zlim. (que j’ai prise égale à 18 km dans mes études), on a un rayonnement entrant dans l’atmosphère qui est TET. Alors, d’après (6.18), le rayonnement descendant à une altitude z est donné par
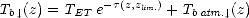 | (6.20) |
avec
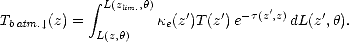 | (6.21) |
Par conséquent, Tb au niveau de la mer est donné par
au niveau de la mer est donné par
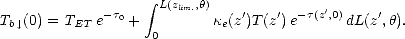 | (6.22) |
Ce rayonnement va être réfléchi par la surface océanique vers le radiomètre et va s’ajouter au rayonnement de la surface océanique. Le rayonnement entrant à la limite inférieure de l’atmosphère (i.e. en z = 0 km) est donné par
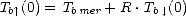 | (6.23) |
où R est le coefficient de reflexion de la surface de la mer. J’ai négligé l’effet de la rugosité de petite
échelle et par conséquent j’ai pris R = RFr, car le rayonnement Tb (0) est relativement faible. J’ai
quantifié l’effet des grandes vagues sur Tb
(0) est relativement faible. J’ai
quantifié l’effet des grandes vagues sur Tb (0) dans la section 6.3.2.
(0) dans la section 6.3.2.
D’après (6.12) et (6.23), le rayonnement ascendant à une altitude z est donné par
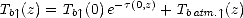 | (6.24) |
avec
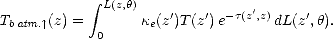 | (6.25) |
On détermine la température apparente à une altitude z en identifiant (6.1) et (6.24). Il vient
Pour résoudre les équations (6.26), (6.27), et (6.28), on a besoin des profils verticaux de la
température T(z) et du coefficient d’absorption  e(z), duquel on va tirer le profil de l’épaisseur optique
e(z), duquel on va tirer le profil de l’épaisseur optique
 (0, z) et l’épaisseur optique totale
(0, z) et l’épaisseur optique totale  0 d’après respectivement (6.17) et (6.19). Pour le profil T(z), j’ai
utilisé un profil de type adiabatique donné par la relation suivante
0 d’après respectivement (6.17) et (6.19). Pour le profil T(z), j’ai
utilisé un profil de type adiabatique donné par la relation suivante
![T (z) = Max [- 50,T(0)- g z]
a](plan_html540x.gif) | (6.29) |
|
|
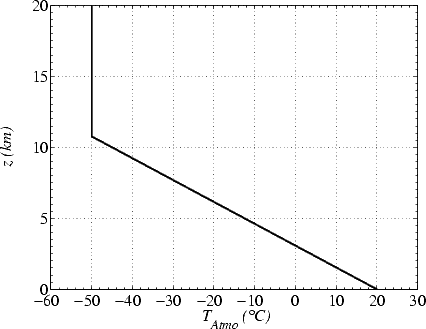
où T est en o C, z en km et 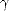 a = -6.5 oC.km-1 est le gradient adiabatique. Le profil T(z) est illustré
sur la figure 6.7 pour T(0) = 20oC. Le coefficient d’absorption
a = -6.5 oC.km-1 est le gradient adiabatique. Le profil T(z) est illustré
sur la figure 6.7 pour T(0) = 20oC. Le coefficient d’absorption  e(z) dépend des interactions entre l’onde
EM et les molécules de l’atmosphère.
e(z) dépend des interactions entre l’onde
EM et les molécules de l’atmosphère.
L’atmosphère est composée de plusieurs gaz dont les molécules vont intéragir avec les ondes EM traversant le milieu. En effet, l’énergie interne d’une molécule est déterminée par ses états d’énergie électronique, vibrationnelle, et rotationnelle. La molécule est susceptible de passer d’un niveau d’énergie à un autre par absorption (ou émission) d’une onde EM de même énergie que celle gagnée (ou perdue) par la molécule lors du changement d’état. Les niveaux d’énergie étant quantifiés pour chacun de ces états, il existe des fréquences discrètes auxquelles les ondes peuvent intéragir avec une molécule. Le spectre d’absorption (ou d’emission) d’une molécule est donc théoriquement constitué de raies à ces fréquences de résonnance. En réalité, dans l’atmosphère, les molécules sous forme de gaz sont en mouvement permanent à cause de l’agitation thermique et autres perturbations. Les raies d’absorption du spectre sont donc élargies et il existe différentes fonctions pour modéliser la forme de ces raies (i.e. l’intensité de l’absorption en fonction de la fréquence) ([90 ]). Le spectre d’absorption variant avec la pression et la température, il va dépendre de l’altitude.
|
|
J’ai utilisé le millimeter-wave Propagation Model (MPM93) proposé par Liebe et al. ([54]) pour la
définition des raies d’absorption. Ce modèle prend en compte l’absorption par l’oxygène (O2) et la vapeur
d’eau (H2 O) entre 1 et 1000 GHz, l’absorption par les autres composants atmosphériques étant
négligeable en hyperfréquences ([90]). Le spectre est composé de 44 raies et d’une composante non
résonnante pour l’O2, ainsi que de 34 raies et d’un continuum empirique pour H2O. Le coefficient
d’absorption total est déterminé par la somme  e(z) =
e(z) =  e(O2)(z) +
e(O2)(z) +  e(H2O)(z) et est fonction de
e(H2O)(z) et est fonction de  0, la
fréquence de l’onde EM, T(z), P(z), la pression atmosphérique et Hr(z) l’humidité relative.
Le coefficient d’absorption au niveau de la mer
0, la
fréquence de l’onde EM, T(z), P(z), la pression atmosphérique et Hr(z) l’humidité relative.
Le coefficient d’absorption au niveau de la mer  e(0) dans le domaine hyperfréquence est
illustré sur la figure 6.8. À 1.41 GHz, il est de l’ordre de 6.10-3 dB.km-1. Il est beaucoup
plus faible en bande L qu’aux plus hautes fréquences et beaucoup moins sensible à la vapeur
d’eau.
e(0) dans le domaine hyperfréquence est
illustré sur la figure 6.8. À 1.41 GHz, il est de l’ordre de 6.10-3 dB.km-1. Il est beaucoup
plus faible en bande L qu’aux plus hautes fréquences et beaucoup moins sensible à la vapeur
d’eau.
Pour déterminer le profil vertical de  e(z), je me suis fixé un profil vertical pour la pression de la
forme suivante
e(z), je me suis fixé un profil vertical pour la pression de la
forme suivante
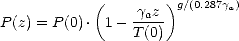 | (6.30) |
et qui est illustré sur la figure 6.9 pour P(0) = 1013 mbars. L’humidité relative Hr(z) (i.e. le rapport entre la pression partielle de vapeur d’eau et la pression de vapeur saturante) est prise constante avec l’altitude z.
Les profils verticaux de  e(O2) et
e(O2) et  e(H2O) en bande L sont reportés sur la figure 6.10 pour des
conditions atmosphériques variées. Dans la suite de cette section, les paramètres atmosphériques seront
fixés à P(0) = 1013 mb, T(0) = 20oC et Hr(0) = 70%. L’influence de ces paramètres sur la
température de brillance et sur l’épaisseur optique atmosphérique sera quantifiée dans la section
6.3.1.
e(H2O) en bande L sont reportés sur la figure 6.10 pour des
conditions atmosphériques variées. Dans la suite de cette section, les paramètres atmosphériques seront
fixés à P(0) = 1013 mb, T(0) = 20oC et Hr(0) = 70%. L’influence de ces paramètres sur la
température de brillance et sur l’épaisseur optique atmosphérique sera quantifiée dans la section
6.3.1.
|
|
Le coefficient d’absorption de la vapeur d’eau en bande L est de l’ordre de 20 fois plus faible que celui de l’oxygène, même pour 100% d’humidité relative. Par conséquent, les effets atmosphériques en bande L sont dominés par l’oxygène. L’absorption diminue très rapidement avec l’altitude, elle se produit dans les premiers kilomètres.
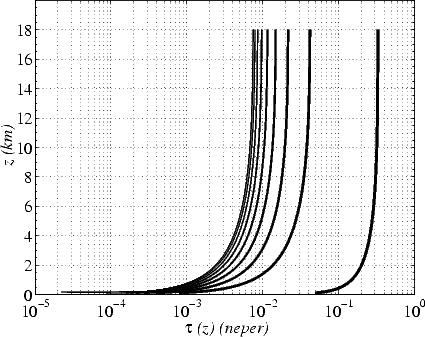
Le profil de l’épaisseur optique  (0,z) dérivé du profil des coefficients d’absorption d’après (6.17), est
reporté sur la figure 6.11 pour plusieurs angles d’incidence: il varie très rapidement sur les cinq premiers
kilomètres et atteint très vite une valeur asymptotique. L’épaisseur optique totale
(0,z) dérivé du profil des coefficients d’absorption d’après (6.17), est
reporté sur la figure 6.11 pour plusieurs angles d’incidence: il varie très rapidement sur les cinq premiers
kilomètres et atteint très vite une valeur asymptotique. L’épaisseur optique totale  0 est très faible pour
la plupart des angles d’incidence et est de l’ordre de 10-2 nepers (sauf près des incidences rasantes).
L’atmosphère en bande L est quasiment transparente. Cette faible épaisseur optique a plusieurs
conséquences (sauf pour les incidences rasantes):
0 est très faible pour
la plupart des angles d’incidence et est de l’ordre de 10-2 nepers (sauf près des incidences rasantes).
L’atmosphère en bande L est quasiment transparente. Cette faible épaisseur optique a plusieurs
conséquences (sauf pour les incidences rasantes):
 0) induit une faible diminution du
rayonnement [1 - exp(-
0) induit une faible diminution du
rayonnement [1 - exp(- 0)], de l’ordre de 0.01 (i.e. de 1%) sur toute l’épaisseur
atmosphérique.
0)], de l’ordre de 0.01 (i.e. de 1%) sur toute l’épaisseur
atmosphérique.
 e(z) . T(z) est le plus élevé, en l’occurrence par les couches atmosphériques les
plus basses (voir les figures 6.7 et 6.10). Ceci implique que Tbatm.
e(z) . T(z) est le plus élevé, en l’occurrence par les couches atmosphériques les
plus basses (voir les figures 6.7 et 6.10). Ceci implique que Tbatm. (zlim.) et Tbatm.
(zlim.) et Tbatm. (0) vont
être essentiellement sensibles aux conditions atmosphérique proches de la surface de la mer.
(0) vont
être essentiellement sensibles aux conditions atmosphérique proches de la surface de la mer.
 (zlim.) et Tbatm.
(zlim.) et Tbatm. (0) sont quasiment identiques.
(0) sont quasiment identiques.
|
|
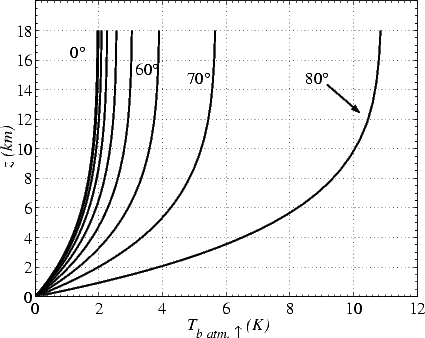
La figure 6.12 illustre Tbatm. (z) pour plusieurs angles d’incidence. Tbatm.
(z) pour plusieurs angles d’incidence. Tbatm. (0) (non montrée) est
identique à T batm.
(0) (non montrée) est
identique à T batm. (zlim.). Les Tbatm. sont de quelques Kelvins et ne peuvent être négligées. Elles
augmentent fortement quands on se rapproche de l’incidence rasante. Enfin, la Tbatm.
(zlim.). Les Tbatm. sont de quelques Kelvins et ne peuvent être négligées. Elles
augmentent fortement quands on se rapproche de l’incidence rasante. Enfin, la Tbatm. varie sensiblement
dans les 10 premiers km ; par conséquent, il faudra prendre en compte l’altitude pour les mesures faites à
partir d’un avion.
varie sensiblement
dans les 10 premiers km ; par conséquent, il faudra prendre en compte l’altitude pour les mesures faites à
partir d’un avion.
|
|
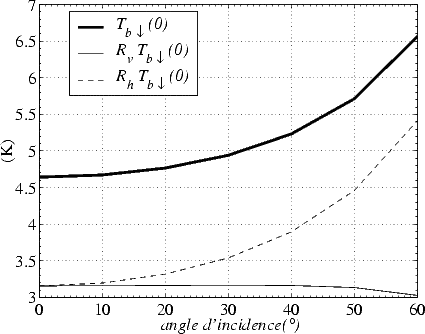
La figure 6.13 illustre Tb (0) en fonction de l’angle d’incidence, ainsi que Tb
(0) en fonction de l’angle d’incidence, ainsi que Tb (0) une fois réfléchie à la
surface de l’océan. Alors que les effets atmosphériques de la basse atmosphère ne sont pas polarisés, la
contribution de l’atmosphère à TAp sera polarisée de par la réflexion du rayonnement descendant à la
surface de l’océan. La variation du rayonnement atmosphérique réfléchi avec l’incidence dans une
polarisation donnée est inversée par rapport à celle de Tbmer: dans le cas de l’atmosphère, le coefficient de
reflexion détermine la fraction de puissance radiative renvoyée vers le radiomètre alors que dans le
cas de T bmer , il détermine la fraction de puissance qui n’est pas émise. L’atténuation des
rayonnements Rv . Tb
(0) une fois réfléchie à la
surface de l’océan. Alors que les effets atmosphériques de la basse atmosphère ne sont pas polarisés, la
contribution de l’atmosphère à TAp sera polarisée de par la réflexion du rayonnement descendant à la
surface de l’océan. La variation du rayonnement atmosphérique réfléchi avec l’incidence dans une
polarisation donnée est inversée par rapport à celle de Tbmer: dans le cas de l’atmosphère, le coefficient de
reflexion détermine la fraction de puissance radiative renvoyée vers le radiomètre alors que dans le
cas de T bmer , il détermine la fraction de puissance qui n’est pas émise. L’atténuation des
rayonnements Rv . Tb (0) et Rh . Tb
(0) et Rh . Tb (0) (non montrée) lors de la remontée vers le radiomètre est peu
sensible (moins de 0.1 K pour
(0) (non montrée) lors de la remontée vers le radiomètre est peu
sensible (moins de 0.1 K pour  < 60o) car ces rayonnements sont faibles (quelques Kelvins).
Par contre, l’atténuation va jouer un rôle sensible sur la Tbmer (de 0.7 K au nadir à plus
de 2 K à 60o d’incidence et en V-pol, voir la figure 6.14) car celle-ci est de l’ordre de 100
K.
< 60o) car ces rayonnements sont faibles (quelques Kelvins).
Par contre, l’atténuation va jouer un rôle sensible sur la Tbmer (de 0.7 K au nadir à plus
de 2 K à 60o d’incidence et en V-pol, voir la figure 6.14) car celle-ci est de l’ordre de 100
K.
La contribution atmosphérique et du fond cosmologique au signal radiométrique (i.e. TAp - Tbmer) est de plusieurs Kelvins au nadir (voir la figure 6.15). Quand l’angle d’incidence augmente, la contribution en V-pol reste quasiment constante alors que celle en H-pol augmente fortement. Cette contribution varie sensiblement avec l’altitude dont il faut par conséquent tenir compte. Pour prendre en compte les effets parasites pour SMOS, on pourrait utiliser des estimations des conditions atmosphériques issues de modèles météorologiques. Pour déterminer la précision de la correction résultante, il faut évaluer la sensibilité des effets atmosphériques aux paramètres atmosphériques.