En chaque point de la surface océanique, on peut définir des pentes Sx et Sy le long de deux directions de
références 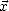 et
et 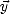 orthogonales entre elles en assimilant localement la surface à un plan (voir la
figure 7.36). La surface étant décrite statistiquement, on va associer à chaque couple de pentes
(Sx dSx , Sy dSy ) une probabilité dP(Sx,Sy), où P(Sx,Sy) est la fonction de densité de probabilité
(FDP) des pentes. J’ai utilisé, comme proposé dans [102], une FDP gaussienne 2D définie
par
orthogonales entre elles en assimilant localement la surface à un plan (voir la
figure 7.36). La surface étant décrite statistiquement, on va associer à chaque couple de pentes
(Sx dSx , Sy dSy ) une probabilité dP(Sx,Sy), où P(Sx,Sy) est la fonction de densité de probabilité
(FDP) des pentes. J’ai utilisé, comme proposé dans [102], une FDP gaussienne 2D définie
par
![1 [ 1((S )2 (S )2)]
P (Sx,Sy) =-------exp - - -x- + -y- ,
2psxsy 2 sx sy](plan_html176x.gif) | (4.23) |
où  x 2 et
x 2 et  y 2 sont les variances des pentes respectivement le long de
y 2 sont les variances des pentes respectivement le long de 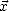 et de
et de 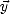 , c’est à dire
, c’est à dire
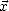 et
et 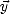 orthogonales entre elles en assimilant localement la surface à un plan (voir la
figure 7.36). La surface étant décrite statistiquement, on va associer à chaque couple de pentes
(Sx dSx , Sy dSy ) une probabilité dP(Sx,Sy), où P(Sx,Sy) est la fonction de densité de probabilité
(FDP) des pentes. J’ai utilisé, comme proposé dans [102], une FDP gaussienne 2D définie
par
orthogonales entre elles en assimilant localement la surface à un plan (voir la
figure 7.36). La surface étant décrite statistiquement, on va associer à chaque couple de pentes
(Sx dSx , Sy dSy ) une probabilité dP(Sx,Sy), où P(Sx,Sy) est la fonction de densité de probabilité
(FDP) des pentes. J’ai utilisé, comme proposé dans [102], une FDP gaussienne 2D définie
par
![1 [ 1((S )2 (S )2)]
P (Sx,Sy) =-------exp - - -x- + -y- ,
2psxsy 2 sx sy](plan_html176x.gif)

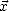 et de
et de 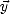 , c’est à dire
, c’est à dire
