Next: 3. Le théorème de
Up: 2. Principes fondamentaux de
Previous: 2.2 Fondements mathématiques :
Contenu
Le principe d'interférométrie qui prédomine dans la synthèse
d'ouverture est parfaitement illustré par l'expérience des trous d'Young
Young, dont le dispositif est décrit par la figure 2.6.
Cet exemple permet de se familiariser intuitivement avec les phénomènes
plus complexes qui seront étudiés par la suite, tout en faisant émerger
des relations importantes pour la suite, comme le théorème de VAN
CITTERT-ZERNIKE, à la base de tout
le travail de reconstruction en synthèse d'ouverture.
Une source primaire 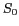 éclaire un masque
percé de deux trous et situé à une distance
éclaire un masque
percé de deux trous et situé à une distance 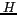 . La figure d'interférence est observée
sur un écran placé à une distance
. La figure d'interférence est observée
sur un écran placé à une distance 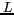 des trous. Les
proportions suivantes seront considérées par la suite :
des trous. Les
proportions suivantes seront considérées par la suite :
- le diamètre des trous est négligeable devant
toutes les autres dimensions.
- la distance D entre les trous est négligeable
devant les longueurs 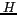 et
et 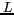 .
.
- la largeur de la figure d'interférence est
petite devant les longueurs 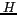 et
et 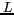 .
.
Etant données ces hypothèses nécessaires à l'obtention
d'interférences, l'étude est menée dans le plan du schéma
et les positions des sources sont reportées sur l'axe 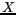 .
.
D'après le principe de
HUYGENS, chaque trou placé en 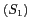 et
et 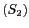 devient une source secondaire au passage de l'onde issue de
devient une source secondaire au passage de l'onde issue de
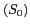 . Le champ électromagnétique
. Le champ électromagnétique
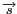 arrivant sur
l'écran est donc la somme des deux champs
arrivant sur
l'écran est donc la somme des deux champs
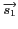 et
et
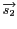 :
:
où 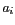 et
et 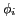 sont l'amplitude et la phase de l'onde
issue de
sont l'amplitude et la phase de l'onde
issue de 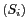 se propageant le long de
se propageant le long de
 , avec
, avec
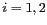 . La pulsation
. La pulsation 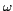 est telle que
est telle que
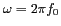 , avec
, avec 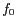 fréquence du champ émis en
fréquence du champ émis en 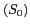 et
et
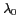 sa longueur d'onde.
sa longueur d'onde.
L'intensité 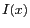 mesuré en
mesuré en 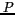 est définie par :
est définie par :
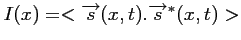 |
(2.27) |
En supposant les amplitudes des ondes secondaires égales à
l'amplitude 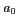 de l'onde primaire :
de l'onde primaire :
où 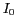 est l'intensité de la source
est l'intensité de la source 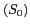 .
.
La phase
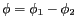 est liée à la différence
de marche
est liée à la différence
de marche 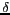 entre les chemins
entre les chemins 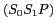 et
et 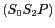 :
:
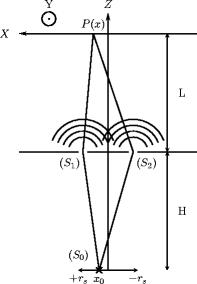
Figure 2-6:
Dispositif de l'expérience des trous d'Young : une
source ponctuelle 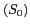 , placée en
, placée en 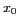 , ou étendue entre
, ou étendue entre
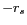 et
et  , rayonne en direction d'un masque,
éloigné d'une distance
, rayonne en direction d'un masque,
éloigné d'une distance 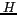 et percé de deux trous
et percé de deux trous 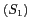 et
et 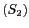 . Une figure d'interférence apparaît sous
certaines conditions sur un écran placé à une distance
. Une figure d'interférence apparaît sous
certaines conditions sur un écran placé à une distance
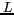 du masque. L'intensité des raies est mesurée au point
du masque. L'intensité des raies est mesurée au point
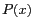 , le long de l'axe
, le long de l'axe 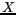 .
.
Dans ce cas, 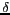 ne dépend que de
ne dépend que de
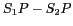 , avec :
, avec :
Pour 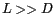 et
et 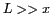 , on peut appliquer l'approximation
, on peut appliquer l'approximation
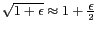 :
:
soit :
Donc d'après les relations (2.29) et (2.30),
l'intensité au point P résultant de l'interférence d'une source
ponctuelle placée en 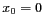 est :
est :
![$\displaystyle I(x) = 2I_0 \left[1 + \cos \left(\frac{\displaystyle 2 \pi}{\lambda_0} \frac{Dx}{L} \right)\right]$](img314.gif) |
(2.38) |
Dans ce cas, 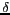 dépend aussi des chemins
dépend aussi des chemins 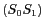 et
et 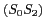 :
:
Pour 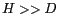 et
et 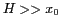 , on peut appliquer l'approximation
, on peut appliquer l'approximation
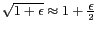 :
:
soit :
Donc d'après les relations (2.29) et (2.30),
l'intensité au point P résultant de l'interférence d'une source
ponctuelle placée en
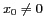 est :
est :
![$\displaystyle I(x) = 2I_0 \left[1 + \cos \left(\frac{\displaystyle 2 \pi}{\lambda_0} \left(\frac{Dx}{L} + \frac{Dx_0}{H} \right)\right)\right]$](img330.gif) |
(2.45) |
La figure d'interférence d'une source étendue est
la somme en intensité des figures d'interférences des
sources ponctuelles constituant la source
étendue. L'intensité mesurée en P est donc :
où 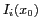 est l'intensité élémentaire émise par chaque
source ponctuelle. L'intensité totale
est l'intensité élémentaire émise par chaque
source ponctuelle. L'intensité totale 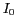 de la source étendue est
donc telle que :
de la source étendue est
donc telle que :
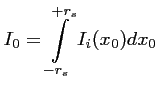 |
(2.48) |
et l'intensité élémentaire normalisée
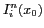 est définie par :
est définie par :
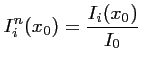 |
(2.49) |
La relation (2.46) devient donc :
Puisque
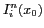 est réel et positif, cette relation
peut aussi s'écrire :
est réel et positif, cette relation
peut aussi s'écrire :
Les relations (2.53) et (2.54) font intervenir
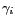 , le degré complexe de cohérence spatiale, quantité
complexe telle que
, le degré complexe de cohérence spatiale, quantité
complexe telle que
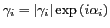 . Ainsi,
l'intensité mesurée en P est de la forme :
. Ainsi,
l'intensité mesurée en P est de la forme :
![$\displaystyle I(x) = 2I_0 \left[1 + \vert \gamma_i \vert \cos \left(\frac{2\pi}{\lambda_0} \frac{Dx}{L} -\alpha_i \right)\right]$](img348.gif) |
(2.55) |
Le facteur de visibilité 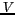 donne une mesure du contraste
des franges d'interférence :
donne une mesure du contraste
des franges d'interférence :
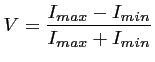 |
(2.56) |
Or d'après (2.55) :
En conclusion, les relations suivantes existent entre le
facteur de visibilité, le degré de cohérence spatiale et la
distribution spatiale d'intensité :
La relation (2.59) est connue sous le nom de théorème
de VAN CITTERT-ZERNIKEVanC1VanC2Zern.
On reconnaît dans cette expression (2.59) une relation
de transformée de Fourier entre le degré de cohérence spatiale
et la distribution spatiale d'intensité. La quantité 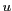 ayant la dimension de l'inverse d'une longueur, elle est appelée
fréquence spatiale, notion qui sera explicitée dans la section suivante.
ayant la dimension de l'inverse d'une longueur, elle est appelée
fréquence spatiale, notion qui sera explicitée dans la section suivante.
Si la distribution d'intensité de la source étendue est
uniforme, alors l'intensité élémentaire est telle
que :
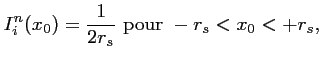 |
(2.61) |
Le degré de cohérence spatiale est :
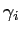 |
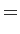 |
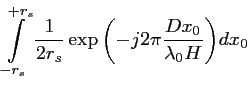 |
(2.62) |
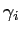 |
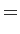 |
![$\displaystyle \frac{\displaystyle 1}{2r_s} \frac{\lambda_0H}{-j2\pi D} \left[\exp{\left(-2j\pi \frac{Dx_0}{\lambda_0H} \right)}\right]^{+r_s}_{-r_s}$](img363.gif) |
(2.63) |
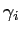 |
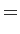 |
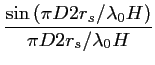 |
(2.64) |
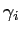 |
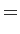 |
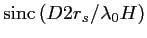 |
(2.65) |
L'intensité mesurée en P est alors :
![$\displaystyle I(x) = 2I_0 \left[1 + \vert \textrm{sinc}\left(D 2r_s/\lambda_0H \right) \vert \cos \left(\frac{2\pi}{\lambda_0} \frac{Dx}{L} \right)\right].$](img366.gif) |
(2.66) |
Ainsi, comme le pressentait FIZEAU en 1868, il est possible de
mesurer le diamètre d'une étoile grâce à sa figure d'interférence.
En effet, il suffit de mesurer la distance entre les trous pour laquelle le facteur
de visibilité est nul, puisque, d'après (2.65),
cette distance est telle que :
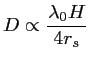 |
(2.67) |
où 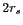 est le diamètre de l'étoile observée.
est le diamètre de l'étoile observée.
La relation (2.66) permet aussi de se rapprocher des propriétés
de la synthèse d'ouverture évoquée dans le chapitre 3 de la première
partie. En effet, en identifiant chacun des trous à une antenne d'un radiomètre
à synthèse d'ouverture, l'augmentation de la distance 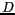 va conduire à une meilleure localisation des franges d'interférences
(terme en cosinus de la relation (2.66)) ce qui peut s'apparenter
à une meilleur résolution spatiale (voir aussi Fig. 2.7),
alors que le contraste sera d'autant plus faible (terme en sinus cardinal de
la relation (2.66)) ce qui peut s'apparenter à une plus
faible résolution radiométrique (voir Fig. 2.8).
va conduire à une meilleure localisation des franges d'interférences
(terme en cosinus de la relation (2.66)) ce qui peut s'apparenter
à une meilleur résolution spatiale (voir aussi Fig. 2.7),
alors que le contraste sera d'autant plus faible (terme en sinus cardinal de
la relation (2.66)) ce qui peut s'apparenter à une plus
faible résolution radiométrique (voir Fig. 2.8).
Figure 2.7: Variation de l'intensité sur une figure
d'interférence obtenue par une expérience de trous d'Young (trait
plein) : cas d'une source étendue. La distance entre deux maximas est
fonction de la distance 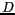 entre les trous : lorsque cette distance augmente, les franges se
rapprochent et sont mieux localisées (tirets).
entre les trous : lorsque cette distance augmente, les franges se
rapprochent et sont mieux localisées (tirets).
|
|
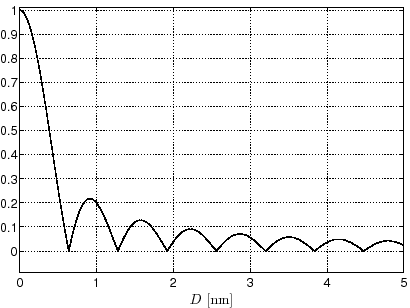
Figure 2.8: Variation de la visibilité en fonction de
la distance entre les trous d'une expérience d'Young : cas d'une source
étendue. La distance entre deux minima, correspondant à la disparition
de la figure d'interférence, dépend de l'étendue 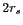 de la source.
de la source.
|
|
Biographie(s)
FIZEAU, Armand Hippolyte Louis
(23 Septembre 1819, Paris, France- 18 Septembre 1896, Venteuil, France)Fizeau.eps
Fils d'un professeur à la faculté de médecine, Fizeau débute
des études de médecine au Collège Stanislas, interrompues par
une santé fragile. Il suit alors les cours d'astronomie de FRANÇOIS
ARAGO à l'observatoire de Paris, ceux d'optique
de VICTOR REGNAULT et, à l'aide des notes
de cours que lui fait parvenir son frère, ceux dispensés à l'Ecole
Polytechnique. En 1839, il perfectionne la dagguerréotypie, améliorant
son temps de vie grâce à l'utilisation de sels d'or et en renforçant
le contraste de l'image.
En 1845, il débute une collaboration fructueuse avec FOUCAULT.
Ils réalisent ensemble le premier dagguerréotype de la surface de
soleil. Obtenant des franges dagguerréotype des franges d'interférence
à partir d'une source de chaleur, ils illustrent la nature semblable de
la lumière et de la chaleur.
En 1848, Fizeau démontre que le son en provenance d'une source mobile sera
perçu différemment par un témoin immobile selon la direction
de son mouvement : si la source se rapproche, le son est de plus en plus aigu,
si elle s'éloigne, le son est de plus en plus grave. Il en est de même
pour la lumière, la lumière d'une source mobile se rapprochant étant
décalée vers le violet, celle d'une source s'éloignant étant
décalée vers le rouge. Cette effet, nommé Doppler-Fizeau, du
nom du physicien arrivé indépendamment à la même conclusion,
permet, après les travaux complémentaires de KICHHOFF
et BUNSEN, d'étudier le mouvement des astres.
En 1849, il donne une bonne approximation de la vitesse de la lumière (315000 km/s)
grâce à un système ingénieux. Un rayon lumineux est projeté
à travers une roue dentée en direction d'un miroir placé à
une très grande distance. Pour certaines vitesses de la roue, le rayon
passe entre deux dents, est réfléchi par le miroir et revient à
sa source. La durée de ce parcours, et donc la vitesse de la lumière,
est lié à la vitesse de la roue dont on mesure la vitesse de rotation.
Une version améliorée de ce dispositif permettra à ALFRED
CORNU, en 1870, d'obtenir une valeur très précise
de la vitesse de la lumière.
Alors que la communauté scientifique croit encore à l'existence de
l'éther , support invisible de la propagation de la lumière, FRESNEL
fait l'hypothèse qu'un corps en mouvement dans cet éther, l'entraîne
en partie dans sa course. Fizeau confirme cette hypothèse en 1851, pourtant
faite sur des bases fausses, grâce là encore à l'interférométrie.
Il montre qu'un rayon lumineux projeté dans un tuyau dans lequel circule
de l'eau, se propage moins vite dans le sens opposé au courant.
MICHELSON, Albert Abraham
(19 Décembre 1852, Strzelno, Pologne - 9 Mai 1931, Pasadena, Californie,
Etats-Unis)michelson.eps
Alors âgé de trois ans, Michelson suit sa famille qui quitte la Pologne
pour San Francisco, Californie en 1855. A 17 ans, il entre à l'Académie
Navale à Annapolis, Maryland, où il se trouve plus d'affinité
avec les sciences qu'avec la mer. Diplômé en 1873, il enseigne les
sciences dans cette même académie jusqu'en 1879.
Dès 1878, Michelson débute la course qu'il mènera en tête
jusqu'à la fin de sa vie : la mesure toujours plus précise de la vitesse
de la lumière (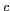 , célérité). Il est dit qu'il réalise sa première
mesure à l'aide d'un équipement valant moins de 10 Dollars! Ressentant
le besoin de se perfectionner en optique, il part pour l'Europe en 1880 et passe
deux ans à Berlin, Heidelberg et Paris.
, célérité). Il est dit qu'il réalise sa première
mesure à l'aide d'un équipement valant moins de 10 Dollars! Ressentant
le besoin de se perfectionner en optique, il part pour l'Europe en 1880 et passe
deux ans à Berlin, Heidelberg et Paris.
A Berlin, il construit son premier interféromètre. Ce dispositif est
principalement composé de deux bras perpendiculaires : un rayon issu d'une
source éloignée est séparé en deux par un miroir semi-argenté.
Chacun des deux nouveaux rayons se propagent le long des bras, se réfléchissent
sur des miroirs fixés à leur extrémité et viennent interférer
après avoir été recombinés. Tout tient à l'un des deux
miroirs qui est mobile et à la précision, de l'ordre de la longueur
d'onde du signal étudié, avec laquelle il est déplacé. La
grande qualité de Michelson était la subtilité des dispositifs
qu'il mettait en place, subtilité telle qu'il a parfois été le
seul à pouvoir les faire fonctionner.
Avec l'aide du chimiste américain WILLIAMS MORLEY,
il est à l'origine d'un non résultat éclatant. Le but de
l'expérience de Morley-Michelson est de démontrer l'existence de l'éther
: la Terre entraînant l'éther avec elle, et si l'un des bras de l'interféromètre
est orienté dans le sens de son mouvement, la durée du trajet des
deux rayons se propageant le long de chacun des bras doit être différent
et donc produire des franges. A partir de 1887 et devant l'absence de résultat,
Michelson n'a cessé d'améliorer la sensibilité de son dispositif,
sans pour autant obtenir de frange. Ce non résultat a permis d'infirmer
l'hypothèse de l'éther et a contribué à confirmer la théorie
de la relativité établie par ALBERT EINSTEIN.
En 1893, partisan de calibrer le mètre étalon d'après une longueur
d'onde donnée (idée adoptée en 1960), il donne une mesure du
mètre en fonction de la longueur d'onde du cadmium. En 1920, il mesure
le diamètre de Betelgeuse à l'aide d'un interféromètre et
en 1923, à la tête d'un dispositif incluant deux pics séparés
d'un quarantaine de kilomètres, un prisme octogonal sur l'un, un miroir
sur l'autre, et la mesure, par triangulation, au quart de pouce près, de
la distance les séparant, il établit une nouvelle valeur pour 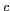 à 299 798 km/s.
à 299 798 km/s.
Pour sa dernière expérience, il utilisa un tube dans lequel le vide
régnait : la lumière y effectuait des allers-retours jusqu'à
parcourir près de 16 km. Les résultats parus en 1933 donnaient
une vitesse de 299 774 km/s, soit moins de 2 km/s d'écart avec
la valeur adopté dans les années 70.
YOUNG, Thomas
(13 Juin 1773, Milverton, Angleterre - 10 Mai 1829, Londres, Angleterre)Young.eps
Thomas Young était en enfant précoce, lisant couramment à l'âge
de deux ans et maîtrisant à 16 ans, le latin, le grec ancien et huit
autres langues classiques et modernes. Sa curiosité l'a amené à
s'illustrer dans de nombreux domaines parmi lesquels la médecine, la physique
et l'archéologie.
En 1793, il débute des études de médecine et seulement un an
plus tard, il présente devant la Royal Society les résultats
de ses recherches sur l'accommodation de la forme de la cornée en fonction
de la distance de l'objet observé. Il obtient son diplôme en 1796
et s'installe à Londres en 1799. En 1801, il démontre que l'astigmatie
résulte d'une déficience de la courbure de la cornée. En 1802,
il publie ses travaux sur la théorie de la couleur, connue sous le nom
de théorie de Young-Helmholtz. Il établit que la perception de l'ensemble
des couleurs est due à la stimulation plus ou moins importante de seulement
trois couleurs principales, rouge, vert et bleu.
En 1803, il décrit ses travaux sur l'interférence lumineuse et sur
la formation de franges lorsqu'un rayon traverse un masque percé de deux
trous très fins et très proches. A cette époque, c'est l'hypothèse
corpusculaire émise par ISAAC NEWTON qui
prédomine. Ce dispositif, connu sous le nom d'expérience des trous
d'Young, permettait dès lors d'établir la nature ondulatoire de la
lumière, mais, à cause de l'influence de Newton, cette hypothèse
n'a été prise en compte que près de 15 ans plus tard, à
la suite des travaux d'AUGUSTIN FRESNEL.
Parmi les contributions de Young, on trouve la notion d'énergie comme le
produit de la masse et du carré de la vitesse, celle du travail comme le
produit de la force par une distance, le module d'Young décrivant
l'élasticité d'un solide, et des hypothèses sur les couleurs
des bulles de savons. En 1813, il tente de déchiffrer les hiéroglyphes
égyptiens et travaille sur la Pierre de Rosette à partir de 1814.
En 1823, il publie une comparaison de ses travaux et de ceux de CHAMPOLLION,
tentant par là de contester, sans succès, la primauté de Champollion.
Son Dictionnaire Egyptien est publié à titre posthume en 1830.
FOURIER, Jean Baptiste Joseph
(21 Mars 1768, Auxerre, France - 16 Mai 1830, Paris, France)Fourier.eps
Dès l'âge de 10 ans, Joseph Fourier se retrouve orphelin, ayant perdu
sa mère très tôt, tandis que son père et sa seconde femme
meurt l'un après l'autre.
Il entre alors à l'école de Pallais que dirige le maître de musique
de la cathédrale. En 1780, il entre à l'Ecole Royale Militaire d'Auxerre
où il montre vite de grandes dispositions pour les mathématiques.
Sa première voie est celle des ordres : il entre au séminaire de l'abbaye
bénédictine de Saint-Benoit-sur-Loire. Il reste cependant tiraillé
entre la prêtrise et les mathématiques, écrivant dans une de
ces lettres à BONARD à Paris : Hier j'ai fêté
mes 21 ans, l'âge auquel Newton et Pascal avait déjà acquis assez
de reconnaissance pour atteindre l'immortalité. .
Il ne prononce pas ses voeux et enseigne à partir de 1790 au collège
bénédictin et à l'Ecole Royale Militaire à Auxerre. Alors
qu'il hésite encore entre une vie consacrée à la foi et une carrière
scientifique, le climat politique décide pour lui et il s'implique dans
le comité local de la Révolution. Animé par un espoir d'égalité,
il est sur le point de démissionné alors que la Terreur fait rage,
mais prisonnier des luttes intestines au sein de la Révolution, il est
contraint de rester. Envoyé à Orléans, il fréquente des
factions minoritaires surveillées par le pouvoir en place, ce qui lui vaut
d'être emprisonné en 1794. A la mort de Robespierre, le climat se
détend et il rejoint l'Ecole Normale nouvellement créée en 1795.
Il fait là la connaissance de LAPLACE, LAGRANGE
et MONGE enseignant à l'Ecole Normale. Après un nouveau
passage en prison, de nouveau pour les incidents d'Orléans, il enseigne
à la nouvelle Ecole Polytechnique dirigée par LAZARE CARNOT
et Gaspard Monge. En 1797, il succède à Lagrange à la chaire
d'analyse et de mécanique.
En 1798, il rejoint Napoléon pour sa campagne d'Egypte. Bloqué sur
place à la suite de la bataille du Nil, il administre Le Caire, dirige
les fouilles archéologiques et fonde l'Institut du Caire au sein duquel
il siège, dans le département de mathématiques, en compagnie
de Monge, MALUS... et Napoléon. De retour en France en 1801,
il souhaite reprendre son poste de professeur à l'Ecole Polytechnique mais
Napoléon à d'autres projets pour lui et le nomme Préfet de l'Isère,
en siège à Grenoble. Contre mauvaise fortune bon coeur, il dirige
les travaux de drainage de Bourgoin et la construction d'une voie rapide rejoignant
Grenoble et Turin.
Parallèlement, il rédige de 1804 à 1807 son fameux traité Sur
la propagation de la chaleur dans les corps solides qu'il soumet à
l'Institut de Paris dont le comité de lecture est composé de Lagrange,
Laplace, Monge et LACROIX. Ceux-ci restent très sceptiques
sur la qualité du document et notamment sur le développement des fonctions
en séries trigonométriques. De plus, BIOT lui reproche
de ne pas faire référence à ses propres travaux sur la dérivation
des équations de transfert de chaleur paru en 1804, rejoint bientôt
avec les mêmes objections par Laplace et POISSON. Et lorsque
l'Institut lance une compétition sur la propagation de la chaleur en 1811,
Fourier est le seul à soumettre ses travaux et gagne le prix, sans toutefois
vraiment convaincre.
Alors que Napoléon est envoyé en exil, Fourier, pour éviter une
confrontation périlleuse, le convainc de ne pas passer par Grenoble. Alors
que l'Empereur effectue son retour d'Elbe, Fourier tente de convaincre la population
de prêter allégeance au Roi et s'enfuit de Grenoble. Il trouve cependant
les mots pour expliquer son comportement à Napoléon qui finit par
lui pardonner et le nomme Préfet du Rhone.
De retour à Paris, Fourier est nommé à l'Académie des Sciences
en 1817. En 1822, son essai Théorie analytique de la chaleur paraît
enfin. [bibli]




Next: 3. Le théorème de
Up: 2. Principes fondamentaux de
Previous: 2.2 Fondements mathématiques :
nous
2005-03-31
![]() éclaire un masque
percé de deux trous et situé à une distance
éclaire un masque
percé de deux trous et situé à une distance ![]() . La figure d'interférence est observée
sur un écran placé à une distance
. La figure d'interférence est observée
sur un écran placé à une distance ![]() des trous. Les
proportions suivantes seront considérées par la suite :
des trous. Les
proportions suivantes seront considérées par la suite :
![]() et
et ![]() .
.
![]() et
et ![]() .
.
![]() .
.
![]() et
et ![]() devient une source secondaire au passage de l'onde issue de
devient une source secondaire au passage de l'onde issue de
![]() . Le champ électromagnétique
. Le champ électromagnétique
![]() arrivant sur
l'écran est donc la somme des deux champs
arrivant sur
l'écran est donc la somme des deux champs
![]() et
et
![]() :
:
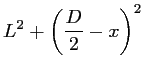
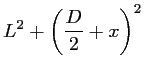
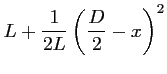
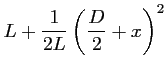
![$\displaystyle \frac{1}{2L} \left[\left(\frac{\displaystyle D}{2} - x \right)^2 - \left(\frac{\displaystyle D}{2} + x \right)^2 \right]$](img312.gif)
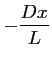
![$\displaystyle I(x) = 2I_0 \left[1 + \cos \left(\frac{\displaystyle 2 \pi}{\lambda_0} \frac{Dx}{L} \right)\right]$](img314.gif)
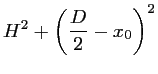
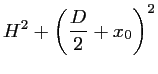
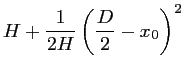
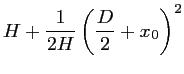
![$\displaystyle \frac{1}{2L} \left[\left(\frac{\displaystyle D}{2} - x \right)^2 ...
...D}{2} - x_0 \right)^2 - \left(\frac{\displaystyle D}{2} + x_0 \right)^2 \right]$](img328.gif)
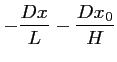
![$\displaystyle I(x) = 2I_0 \left[1 + \cos \left(\frac{\displaystyle 2 \pi}{\lambda_0} \left(\frac{Dx}{L} + \frac{Dx_0}{H} \right)\right)\right]$](img330.gif)
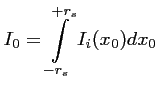
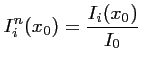
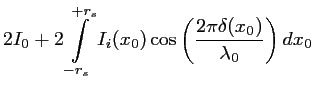
![$\displaystyle 2I_0 \left[1 + \int \limits_{-r_s}^{+r_s} I^n_i(x_0)\cos \left(\frac{\displaystyle 2 \pi \delta (x_0)}{\lambda_0} \right)dx_0 \right]$](img338.gif)
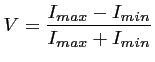
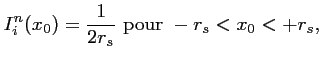
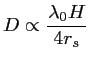
![]() va conduire à une meilleure localisation des franges d'interférences
(terme en cosinus de la relation (2.66)) ce qui peut s'apparenter
à une meilleur résolution spatiale (voir aussi Fig. 2.7),
alors que le contraste sera d'autant plus faible (terme en sinus cardinal de
la relation (2.66)) ce qui peut s'apparenter à une plus
faible résolution radiométrique (voir Fig. 2.8).
va conduire à une meilleure localisation des franges d'interférences
(terme en cosinus de la relation (2.66)) ce qui peut s'apparenter
à une meilleur résolution spatiale (voir aussi Fig. 2.7),
alors que le contraste sera d'autant plus faible (terme en sinus cardinal de
la relation (2.66)) ce qui peut s'apparenter à une plus
faible résolution radiométrique (voir Fig. 2.8).
![\begin{picture}(16,7)(-8,-3)
\rput(0,0){
\begin{tabular}{m{15cm}<{\centering }...
....2,-0.6){$x$\ [nm]}
\rput{90}(-4.55,3.45){$I(x)$}
}
%
%
\par
\end{picture}](img369.gif)