|
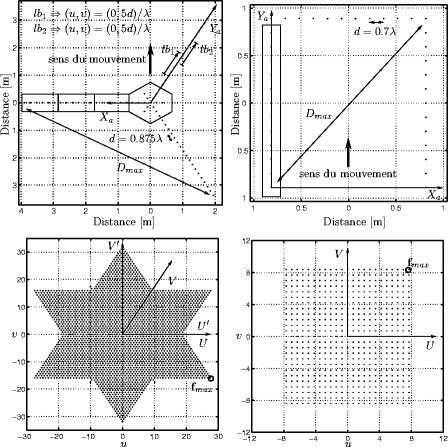
Deux géométries envisageables pour un réseau destiné à l'observation de la Terre sont étudiées ci-dessous : une géométrie en Y, conduisant à un échantillonnage sur un maillage hexagonal et une géométrie en U, conduisant à un échantillonnage sur un maillage cartésien. Les deux grilles étudiées constituent les deux seuls maillages périodiques permettant de paver tout le plan. D'autres géométries, en T ou en L par exemple, changent la forme de la couverture expérimentale mais pas le maillage sous-jacent.

|
Les lignes de base, calculées à partir des positions relatives des
antennes, définissent, dans le domaine de FOURIER, les fréquences
spatiales angulaires pour lesquelles seront effectuées les mesures interférométriques.
Les dimensions finies de l'instrument confinent les mesures à l'intérieur
d'une couverture fréquentielle expérimentale ![]() , dont la forme est caractéristique d'une géométrie
du réseau interférométrique (voir Fig. 4.1,
en bas). Une propriété importante des radiomètres imageurs à
synthèse d'ouverture émerge alors : ce sont des instruments à
bande passante limitée.
, dont la forme est caractéristique d'une géométrie
du réseau interférométrique (voir Fig. 4.1,
en bas). Une propriété importante des radiomètres imageurs à
synthèse d'ouverture émerge alors : ce sont des instruments à
bande passante limitée.
On peut aussi d'ores et déjà remarquer que deux différents
couples d'antennes peuvent engendrer la même fréquence spatiale (voir
les lignes de bases ![]() et
et ![]() sur la figure 4.1 en haut à gauche).
On distinguera alors le nombre de lignes de base et donc de mesures instrumentales,
du nombre de fréquences à l'intérieur de
sur la figure 4.1 en haut à gauche).
On distinguera alors le nombre de lignes de base et donc de mesures instrumentales,
du nombre de fréquences à l'intérieur de ![]() .
.
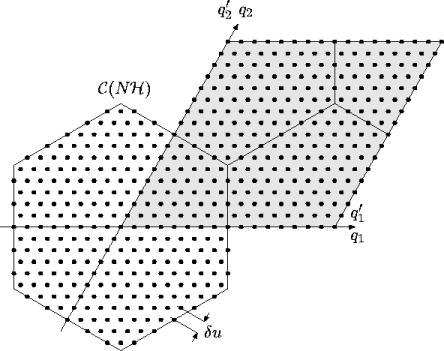
Les mesures réalisées par un réseau en U
sont effectuées à des fréquences spatiales coïncidant avec
les noeuds d'un maillage cartésien. La couverture
fréquentielle expérimentale ![]() a la forme d'un rectangle,
le maillage cartésienne qui la prolonge étant caractérisé
par :
a la forme d'un rectangle,
le maillage cartésienne qui la prolonge étant caractérisé
par :
| (4.1) |
| (4.2) | |||
| (4.3) |
La fréquence la plus grande
![]() est
déterminée par la plus grande distance
est
déterminée par la plus grande distance ![]() entre deux antennes :
entre deux antennes :
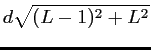 |
(4.4) | ||
| (4.5) | |||
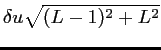 |
(4.6) |
La taille de la maille élémentaire du réseau cartésien est choisie
de façon à contenir entièrement la couverture fréquentielle
![]() . De plus, pour faciliter l'utilisation
d'algorithme de transformée de FOURIER rapide (FFT pour
Fast Fourier Transform),
. De plus, pour faciliter l'utilisation
d'algorithme de transformée de FOURIER rapide (FFT pour
Fast Fourier Transform), ![]() est choisi comme une puissance
de 2. Le réseau cartésien est alors caractérisé par :
est choisi comme une puissance
de 2. Le réseau cartésien est alors caractérisé par :
| (4.7) |
Etant données les dimensions de l'instrument considéré, la
fréquence la plus grande est telle que
![]() et une maille élémentaire comprenant
et une maille élémentaire comprenant
![]() pixels a une taille suffisante pour contenir la bande passante. Toutefois, afin d'obtenir une
représentation plus fine des résultats présentés par la suite, le nombre de
pixels est fixé à
pixels a une taille suffisante pour contenir la bande passante. Toutefois, afin d'obtenir une
représentation plus fine des résultats présentés par la suite, le nombre de
pixels est fixé à
![]() .
.
La figure 4.2 illustre les relations précédentes
pour un instrument comportant 3 antennes par bras. Les surfaces
![]() et
et
![]() des cellules élémentaires
des cellules élémentaires
![]() et
et
![]() des réseaux périodiques sont
respectivement égales à
des réseaux périodiques sont
respectivement égales à
![]() et
et
![]() où
où
![]() .
.
C'est dans ce domaine que les cartes de
températures de brillance sont reconstruites.
Considérons alors
![]() le réseau réciproque
de
le réseau réciproque
de
![]() :
:
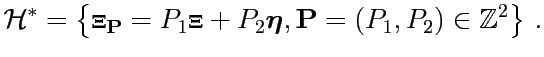 |
(4.8) |
La cellule élémentaire de
![]() est
échantillonnée aux noeuds de
est
échantillonnée aux noeuds de
![]() , le réseau réciproque
de
, le réseau réciproque
de
![]() :
:
| (4.9) |
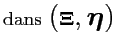 |
(4.10) | ||
| (4.11) |
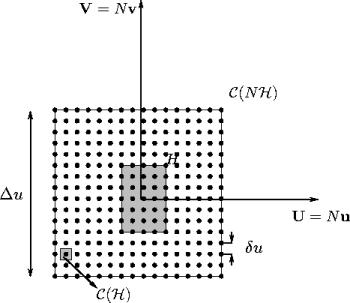
La figure 4.3 illustre les relations précédentes
pour un instrument comportant 3 antennes par bras. Les surfaces
![]() et
et
![]() des cellules élémentaires
des cellules élémentaires
![]() et
et
![]() de ces réseaux périodiques
cartésiens sont respectivement égales à
de ces réseaux périodiques
cartésiens sont respectivement égales à
![]() et
et
![]() .
.
D'après une propriété bien connue des réseaux réciproques, le produit
des surfaces des cellules élémentaires de deux réseaux réciproques est
unitaire :
![]() .
Par conséquent, les relations entre l'intervalle d'échantillonnage
de FOURIER
.
Par conséquent, les relations entre l'intervalle d'échantillonnage
de FOURIER ![]() et l'étendue du champ de
vue
et l'étendue du champ de
vue
![]() d'une part et la largeur de bande
spectrale
d'une part et la largeur de bande
spectrale ![]() et le pas d'échantillonnage dans le
domaine spatial
et le pas d'échantillonnage dans le
domaine spatial
![]() d'autre part sont telles que :
d'autre part sont telles que :
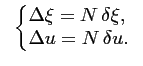 |
(4.12) |
Soient les ![]() entiers,
entiers,
| (4.13) |
| (4.14) |
|
|
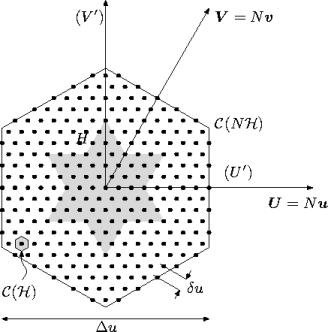
Pour un réseau interférométrique en Y, les
fréquences spatiales ![]() , confinées à l'intérieur d'une
bande passante
, confinées à l'intérieur d'une
bande passante ![]() en forme d'étoile, coïncident
avec les noeuds d'une grille hexagonale Lannesproc. Le traitement des
données interférométriques se fera alors sur des grilles
hexagonales CampsHexa1 CampsHexa2.
en forme d'étoile, coïncident
avec les noeuds d'une grille hexagonale Lannesproc. Le traitement des
données interférométriques se fera alors sur des grilles
hexagonales CampsHexa1 CampsHexa2.
Le choix d'un repère orienté selon ![]() est naturel dès lors que le
maillage est hexagonal. Toutefois, il peut être utile
d'utiliser un repère orthonormé. Le passage d'un système
d'axe à l'autre se fait donc à l'aide des relations
suivantes :
est naturel dès lors que le
maillage est hexagonal. Toutefois, il peut être utile
d'utiliser un repère orthonormé. Le passage d'un système
d'axe à l'autre se fait donc à l'aide des relations
suivantes :
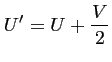 |
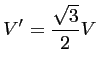 |
(4.15) | |
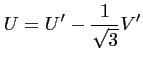 |
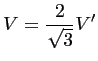 |
(4.16) |
La grille hexagonale
![]() prolongeant la couverture
fréquentielle expérimentale
prolongeant la couverture
fréquentielle expérimentale ![]() est caractérisée ainsi :
est caractérisée ainsi :
| (4.17) |
| (4.18) | |||
| (4.19) | |||
| (4.20) |
La fréquence la plus grande
![]() , que l'on retrouve
aux pointes de l'étoile, est déterminée par la plus grande
distance
, que l'on retrouve
aux pointes de l'étoile, est déterminée par la plus grande
distance ![]() entre deux antennes :
entre deux antennes :
| (4.21) | |||
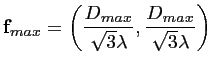 |
(4.22) | ||
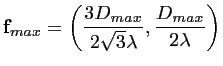 |
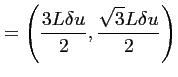 |
(4.23) | |
| (4.24) |
Le réseau est alors caractérisé par :
| (4.25) |
Etant données les dimensions de l'instrument considéré, la
norme de la fréquence la plus grande vaut
![]() et une maille élémentaire
comprenant
et une maille élémentaire
comprenant
![]() pixels a une taille
suffisante pour contenir la bande passante. Toutefois, la
réorganisation du stockage des données de la maille élémentaire (voir paragraphe d.
de cette section) impose de choisir une maille plus étendue
avec
pixels a une taille
suffisante pour contenir la bande passante. Toutefois, la
réorganisation du stockage des données de la maille élémentaire (voir paragraphe d.
de cette section) impose de choisir une maille plus étendue
avec
![]() pixels.
pixels.
Afin d'illustrer les relations précédentes, la cellule élémentaire
de
![]() échantillonnée aux noeuds de
échantillonnée aux noeuds de
![]() est montrée dans la figure 4.4,
pour un instrument ne comptant que 3 antennes par bras. Les surfaces
est montrée dans la figure 4.4,
pour un instrument ne comptant que 3 antennes par bras. Les surfaces
![]() et
et
![]() des cellules élémentaires
des cellules élémentaires
![]() et
et
![]() des réseaux périodiques sont
respectivement égales à
des réseaux périodiques sont
respectivement égales à
![]() et
et
![]() où
où
![]() .
.
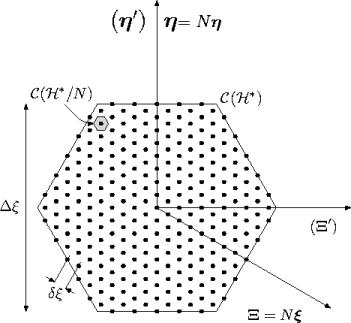
Considérons
![]() le réseau réciproque
de
le réseau réciproque
de
![]() :
:
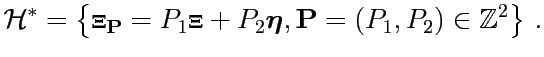 |
(4.26) |
| (4.27) |
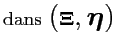 |
(4.28) | ||
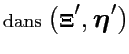 |
(4.29) | ||
| (4.30) |
Afin d'illustrer les relations précédentes, une cellule élémentaire
de
![]() échantillonnées aux noeuds de
échantillonnées aux noeuds de
![]() est montrée sur la figure 4.5,
pour un instrument ne comptant que 3 antennes par bras. Les surfaces
est montrée sur la figure 4.5,
pour un instrument ne comptant que 3 antennes par bras. Les surfaces
![]() et
et
![]() des cellules élémentaires
des cellules élémentaires
![]() et
et
![]() de ces réseaux périodiques
hexagonaux sont respectivement égales à
de ces réseaux périodiques
hexagonaux sont respectivement égales à
![]() et
et
![]() .
.
|
|
De l'expression des aires des cellules élémentaires de chacun des réseaux et de la relation entre les surfaces des réseaux réciproques, il vient dans le cas spécifique des réseaux périodiques hexagonaux :
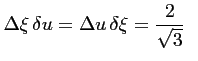 avec avec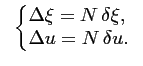 |
(4.31) |
Soient les ![]() entiers,
entiers,
| (4.32) |
| (4.33) |
Les grilles ne sont pas adaptées à l'utilisation des algorithmes de Transformée de FOURIER Rapide (FFT), développés pour des grilles cartésiennes. Une solution consiste en l'implémentation d'un algorithme spécifiquement étudié pour des grilles hexagonales Mersereau. Toutefois, une telle approche condamne son utilisateur à ne pas profiter des avancées faites sur les FFT pour les grilles cartésiennes.
Une autre solution est de redéfinir la maille
élémentaire, en utilisant non pas un hexagone mais le
rhomboïde, maille élémentaire traditionnelle des maillages
hexagonaux en cristallographie Kittel. La réorganisation des
données échantillonnées sur les hexagones
![]() et
et
![]() permet de
construire les losanges
permet de
construire les losanges
![]() et
et
![]() , mieux
adaptés au calcul matriciel et définis ainsi :
, mieux
adaptés au calcul matriciel et définis ainsi :
| (4.34) |
| (4.35) |
|
 |