- a.
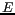 espace des objets
espace des objets
- b.
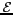 , sous espace de E des fonctions à
bande passante limitée.
, sous espace de E des fonctions à
bande passante limitée.
- c.
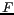 , espace des données
, espace des données
- d. Propriété d'hermiticité des espaces
Les paragraphes suivants décrivent les espaces de travail entre lesquels seront définis les opérateurs intervenant dans la reconstruction EricApod EricMatres. configuration en Y.
Il s'agit de l'espace
des fonctions ![]() de distribution des températures de brillance
échantillonnées qui prennent leurs valeurs
de distribution des températures de brillance
échantillonnées qui prennent leurs valeurs
![]() aux
noeuds
aux
noeuds
![]() de la grille
spatiale
de la grille
spatiale
![]() LannesA LannesB.
LannesA LannesB.
L'espace dual
![]() est l'image de
est l'image de ![]() par l'opérateur de transformée
de FOURIER. Autrement dit, c'est l'espace des transformées de FOURIER
par l'opérateur de transformée
de FOURIER. Autrement dit, c'est l'espace des transformées de FOURIER
![]() prenant leurs valeurs
prenant leurs valeurs
![]() aux noeuds
aux noeuds
![]() de la grille de FOURIER
de la grille de FOURIER
![]() .
.
Les fonctions
![]() à bande limitée dans
à bande limitée dans ![]() , définies comme
étant les fonctions dont la transformée de
FOURIER
, définies comme
étant les fonctions dont la transformée de
FOURIER
![]() est confinée dans la couverture
fréquentielle expérimentale
est confinée dans la couverture
fréquentielle expérimentale ![]() , joue un rôle important dans la
synthèse de FOURIER LannesB. Elles appartiennent au
sous-espace
, joue un rôle important dans la
synthèse de FOURIER LannesB. Elles appartiennent au
sous-espace
![]() de
de ![]() , dont l'image par l'opérateur de
transformée de FOURIER est le sous-espace
, dont l'image par l'opérateur de
transformée de FOURIER est le sous-espace
![]() de
de
![]() .
Les fonctions
.
Les fonctions
![]() prennent leurs
valeurs
prennent leurs
valeurs
![]() aux noeuds
aux noeuds
![]() de la grille de FOURIER uniquement
contenue dans
de la grille de FOURIER uniquement
contenue dans ![]() .
.
Les fréquences spatiales
![]() , associées à
chaque couple d'antennes
, associées à
chaque couple d'antennes ![]() et
et ![]() de l'instrument, appartiennent à une liste
finie
de l'instrument, appartiennent à une liste
finie
![]() dans le domaine de FOURIER :
dans le domaine de FOURIER :
| (4.36) |
D'après les propriétés d'hermiticité de la transformée de FOURIER des
fonctions réelles, et celles des visibilités complexes,
les espace duaux
![]() et
et
![]() peuvent être définis sur la moitié seulement des noeuds des grilles
utilisées. La même remarque vaut pour l'espace des données
peuvent être définis sur la moitié seulement des noeuds des grilles
utilisées. La même remarque vaut pour l'espace des données ![]() et la
liste des fréquences expérimentales
et la
liste des fréquences expérimentales
![]() .
.
Cependant, afin d'introduire confortablement ces espaces et leurs normes, il était préférable de ne faire cette remarque qu'en dernier lieu plutôt que d'introduire une difficulté supplémentaire, et par là même une dose de confusion, dans leur définition.
Ainsi, pour un instrument de type MIRAS possédant ![]() antennes avant et
antennes avant et ![]() antennes arrières par bras, soit
antennes arrières par bras, soit
![]() antennes au total, et
antennes au total, et ![]() pour un instrument de type
HUT2D qui ne possède pas d'antennes arrières, le nombre de visibilités complexes mesurées est
pour un instrument de type
HUT2D qui ne possède pas d'antennes arrières, le nombre de visibilités complexes mesurées est
![]() auquel il convient d'ajouter une mesure réelle à la
fréquence nulle fournie par les NIR , soient
auquel il convient d'ajouter une mesure réelle à la
fréquence nulle fournie par les NIR , soient
![]() visibilités au total. L'espace des
données
visibilités au total. L'espace des
données ![]() est donc isomorphe à
est donc isomorphe à
![]() , et
donc
, et
donc
![]() pour MIRAS et
pour MIRAS et
![]() pour HUT2D.
pour HUT2D.
De même, le nombre de fréquences contenues dans la bande
passante est
![]() pour MIRAS et
pour MIRAS et
![]() pour le HUT2D, auquel
il convient d'ajouter la fréquence nulle. L'espace dual
pour le HUT2D, auquel
il convient d'ajouter la fréquence nulle. L'espace dual
![]() est donc isomorphe à
est donc isomorphe à
![]() , avec
, avec
![]() pour MIRAS et
pour MIRAS et
![]() , soit
, soit
![]() pour MIRAS et
pour MIRAS et
![]() pour HUT2D.
pour HUT2D.
Pour finir, l'espace des objets ![]() est isomorphe à
est isomorphe à
![]() , soit
, soit
![]() (
(![]() ) pour MIRAS et à
) pour MIRAS et à
![]() (
(![]() ) pour HUT2D. De même, compte tenu de la propriété
d'hermiticité,
) pour HUT2D. De même, compte tenu de la propriété
d'hermiticité,
![]() est isomorphe à
est isomorphe à
![]() , soit
, soit
![]() pour MIRAS et à
pour MIRAS et à
![]() pour HUT2D. Le tableau 4.1
résume ces quelques résultats pour MIRAS et HUT2D.
pour HUT2D. Le tableau 4.1
résume ces quelques résultats pour MIRAS et HUT2D.
Le passage du domaine de FOURIER au domaine spatiale, et inversement, est une opération courante en synthèse de FOURIER.
Soit, donc, l'opérateur de transformée de
FOURIER
![]() :
:
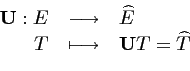 |
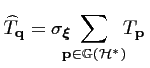 e e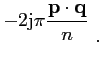 |
(4.37) |
Dès lors que l'on est amené à considérer des instruments à bande passante limitée, il est nécessaire de disposer d'un opérateur permettant compléter avec des zéros la grille contenant les données interférométriques.
Soit, maintenant,
![]() l'opérateur de remplissage de
zéros (zero-padding) au-delà
de la couverture fréquentielle expérimentale
l'opérateur de remplissage de
zéros (zero-padding) au-delà
de la couverture fréquentielle expérimentale ![]() :
:
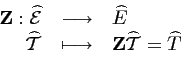 |
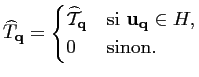 |
(4.38) |
La présence d'un sous-espace des fonctions à bande passante
limitée rend nécessaire la définition d'un projecteur
permettant le passage de ![]() à
à
![]() .
.
Etant données les définitions précédentes, il est
possible d'introduire
![]() :
:
| (4.39) |