L'opérateur de modélisation
![]() joue un rôle central
dans la reconstruction d'image par des méthodes
régularisées. Cette section caractérise l'action de
joue un rôle central
dans la reconstruction d'image par des méthodes
régularisées. Cette section caractérise l'action de
![]() mais
aussi celle de son adjoint
mais
aussi celle de son adjoint
![]() qui intervient dans la définition
de certains opérateurs de reconstruction. La représentation
matricielle de l'opérateur de modélisation est elle aussi
explicitée.
qui intervient dans la définition
de certains opérateurs de reconstruction. La représentation
matricielle de l'opérateur de modélisation est elle aussi
explicitée.
L'opérateur de modélisation est l'opérateur
![]() de l'espace des objets
de l'espace des objets ![]() vers celui des données
vers celui des données ![]() décrivant la relation (3.38)
entre les visibilités complexes et la distribution des températures
de brillance de la scène observée :
décrivant la relation (3.38)
entre les visibilités complexes et la distribution des températures
de brillance de la scène observée :
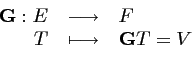 |
(4.40) |
Avant de déterminer l'expression de l'opérateur adjoint
![]() , il est nécessaire d'expliciter la
définition des produits scalaires dans
, il est nécessaire d'expliciter la
définition des produits scalaires dans ![]() et
et ![]() :
:
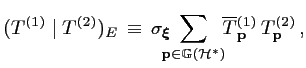 |
(4.42) |
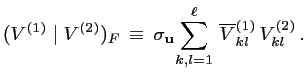 |
(4.43) |
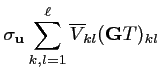 |
(4.44) | ||
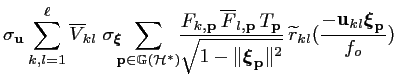 e e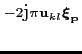 |
(4.45) | ||
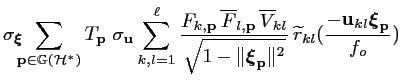 e e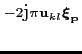 |
(4.46) | ||
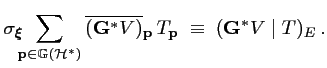 |
(4.47) |
La définition de
![]() , adjoint de l'opérateur de
modélisation
, adjoint de l'opérateur de
modélisation
![]() est donc la suivante :
est donc la suivante :
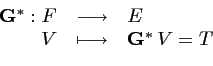 |
(4.48) |
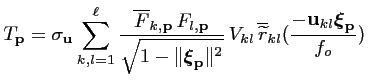 e e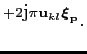 |
(4.49) |
Afin d'assurer le caractère réel des températures de brillance
reconstruites, il est préférable de construire la matrice
![]() , correspondant à l'opérateur de modélisation,
comme une matrice réelle. Ainsi, la première ligne contient des informations
sur la contribution de chaque pixel à la fonction de cohérence spatiale
à la fréquence nulle (valeur réelle de fait). Les
, correspondant à l'opérateur de modélisation,
comme une matrice réelle. Ainsi, la première ligne contient des informations
sur la contribution de chaque pixel à la fonction de cohérence spatiale
à la fréquence nulle (valeur réelle de fait). Les ![]() lignes suivantes contiennent la partie réelle de la contribution
de chaque pixel à la fonction de cohérence spatiale et les
lignes suivantes contiennent la partie réelle de la contribution
de chaque pixel à la fonction de cohérence spatiale et les ![]() dernières lignes contiennent la partie imaginaire de cette
contribution (voir Fig. 4.8).
dernières lignes contiennent la partie imaginaire de cette
contribution (voir Fig. 4.8).
Le principe de construction de cette matrice est alors simple : il s'agit
de calculer la contribution aux visibilités de chacun des pixels composant
la carte des températures ![]() . On parcourt donc la grille d'échantillonnage en simulant une
impulsion unité sur le pixel courant,
. On parcourt donc la grille d'échantillonnage en simulant une
impulsion unité sur le pixel courant,
![]() , la température étant nulle ailleurs.
L'algorithme de construction de
, la température étant nulle ailleurs.
L'algorithme de construction de
![]() est donc le suivant :
est donc le suivant :
Algorithme de construction de
![]()
Do p =
![]()
G[1,p] =
![]()
EndDo
Do b =
![]()
Do p =
![]()
| DXDY | = |
e |
| G[b,p] | = |
|
| G[b+ |
= |
|
|
|
Dimensions
|
Taille
|
Temps de calcul |
|
|
|
|
|
|
MIRAS
|
|
586.6 Mo
|
15 s |
|
|
|
|
|
|
HUT2D
|
|
39.6 Mo
|
1 s |
|
|
|
|
|

De 1941 à 1972, il travaille pour la société AT&T Bell dans le New Jersey, dont il parcourt les couloirs... juché sur un monocycle. En 1948, il révolutionne le domaine de la communication en publiant A Mathematical Theory of Communication dans lequel il suggère un codage de l'information sous la forme de bits, pour binary digit, introduisant la possibilité de transmettre l'information sous une forme discrète et non plus continue.
Lors de la dernière partie de sa carrière, il travaille sur
l'intelligence artificielle. Il développe notamment les premiers programmes
permettant aux machines de jouer aux échecs...et un monocycle
à deux places.

De 1917 à 1934, il est employé de l'American Telephone and Telegraph Company au sein du département de recherche et développement en transmission où il se consacre à l'étude de la transmission de l'image et de la voix par le télégraphe. De 1934 jusqu'à sa retraite en 1954, il travaille pour la société Bell Telephone Laboratories pour laquelle il continue ses recherches en transmission et particulièrement sur les systèmes de transmission. Parmi ses principales contribution, on trouve notamment la première formulation quantitative du bruit thermique ou encore le développement du diagramme de Nyquist, permettant d'établir la stabilité des systèmes en feedback . [bibli]