Next: 5.2 Les fenêtres d'apodisation
Up: 5. Apodisation
Previous: 5. Apodisation
Contenu
La figure 5.1-a représente la distribution 1D 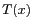 des températures de brillance observées par l'instrument.
La figure 5.1-b montre la transformée de
Fourier
des températures de brillance observées par l'instrument.
La figure 5.1-b montre la transformée de
Fourier
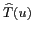 de cette distribution. En considérant que les visibilités
et les températures de brillance sont liées par une simple transformée
de FOURIER, les mesures instrumentales sont les composantes de
Fourier comprises entre
de cette distribution. En considérant que les visibilités
et les températures de brillance sont liées par une simple transformée
de FOURIER, les mesures instrumentales sont les composantes de
Fourier comprises entre 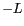 et
et 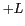 ,
, 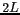 étant la bande passante de l'instrument (voir Fig. 5.1-c)
: autrement dit, le signal dans le domaine de Fourier est multiplié par une
fonction rectangle qui vaut 1 pour
étant la bande passante de l'instrument (voir Fig. 5.1-c)
: autrement dit, le signal dans le domaine de Fourier est multiplié par une
fonction rectangle qui vaut 1 pour
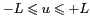 et 0 sinon. Cette multiplication dans le
domaine de Fourier se traduit, dans le domaine spatial, par une convolution par
un sinus cardinal (voir Fig. 5.1-d) : les oscillations de
GIBBS dans la distribution
et 0 sinon. Cette multiplication dans le
domaine de Fourier se traduit, dans le domaine spatial, par une convolution par
un sinus cardinal (voir Fig. 5.1-d) : les oscillations de
GIBBS dans la distribution 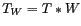 sont la conséquence de cette convolution.
sont la conséquence de cette convolution.
Les notions de fuite radiométrique et de dégradation de la résolution
spatiale émergent de la comparaison de la distribution initiale 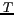 avec la distribution reconstruite
avec la distribution reconstruite 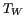 . La première de ces deux sources de dégradation de la
qualité de la reconstruction est due aux oscillations que l'on observe
aux bords des créneaux (voir Fig. 5.2-a) : alors que
la température observée a une valeur constante, la température
reconstruite comporte des variations de l'ordre de 10% autour d'une valeur moyenne.
D'autre part, la dégradation de la résolution spatiale apparaît
clairement dans la difficulté à localiser précisément les
limites du créneau reconstruit (voir Fig. 5.2-b).
. La première de ces deux sources de dégradation de la
qualité de la reconstruction est due aux oscillations que l'on observe
aux bords des créneaux (voir Fig. 5.2-a) : alors que
la température observée a une valeur constante, la température
reconstruite comporte des variations de l'ordre de 10% autour d'une valeur moyenne.
D'autre part, la dégradation de la résolution spatiale apparaît
clairement dans la difficulté à localiser précisément les
limites du créneau reconstruit (voir Fig. 5.2-b).
Puisque ces phénomènes sont causés par une coupure brusque
aux bords de la bande passante, le principe moteur de
l'apodisation consiste à remplacer la fonction rectangle par
des fonctions conduisant à une transition plus douce et
ainsi diminuer l'amplitude des oscillations.
Cependant, ainsi que le montre la figure 5.3, cette
opération a un coût : la meilleure résolution spatiale compte
tenu des caractéristiques de l'instrument est celle obtenue avec la fenêtre
rectangle et l'utilisation de n'importe quelle autre fenêtre conduira a
une dégradation de cette résolution. Le choix de la fenêtre d'apodisation
à appliquer dépend donc des objectifs finaux de la reconstruction
: jusqu'où est-on prêt à dégrader la résolution spatiale
afin d'améliorer la sensibilité radiométrique ? Les facteurs
de mérite des fenêtres, caractérisant leurs propriétés
en terme de résolution ou de sensibilité radiométrique, vont
offrir une aide précieuse quant à ce choix.
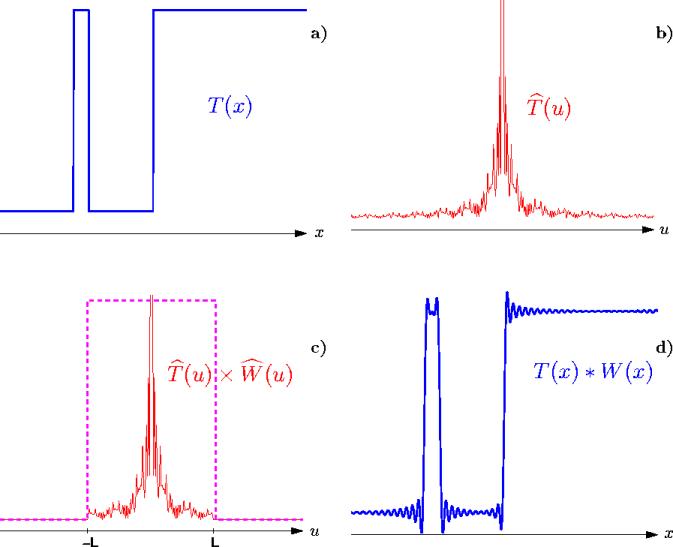
Figure 5.1: Oscillations de GIBBS : a)
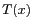 , distribution des
, distribution des  observée. b)
observée. b)
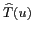 , la transformée de Fourier de
, la transformée de Fourier de 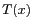 . c)
. c)
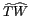 , les mesures instrumentales sont contenues
à l'intérieur d'une bande passante limitée. d)
, les mesures instrumentales sont contenues
à l'intérieur d'une bande passante limitée. d)
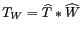 , la distribution de
, la distribution de  reconstruite.
reconstruite.
|
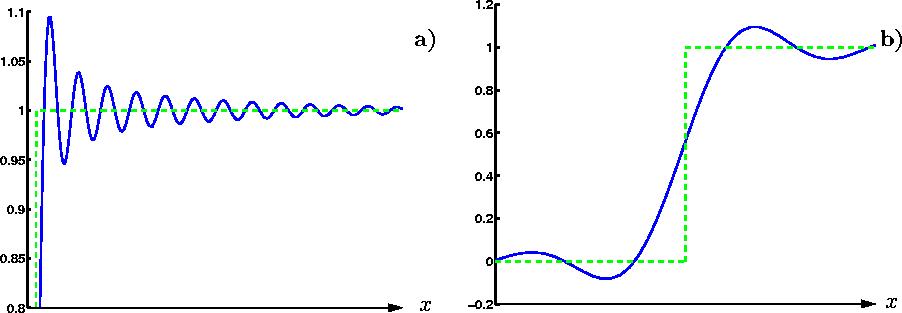
Figure 5.2: Fuite radiométrique et dégradation
de la résolution spatiale : a) La température constante
observée (tirets) est corrompue par des oscillation. b) la
limite entre les deux plateaux reconstruits est moins bien localisée
que dans le cas initial.
|
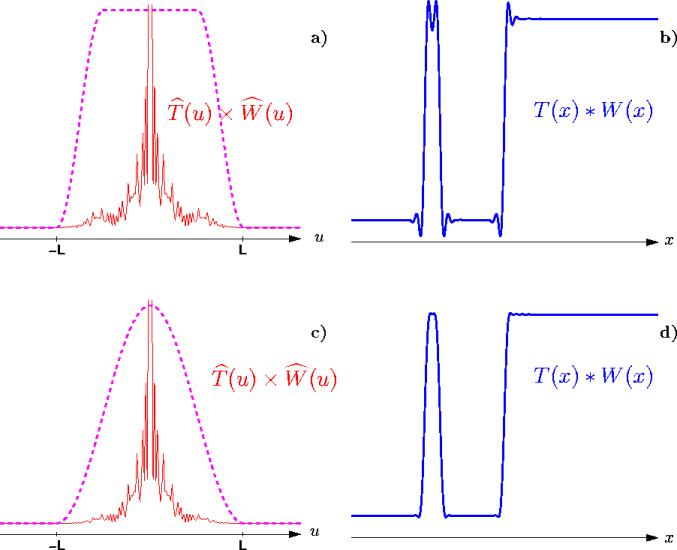
Figure 5.3: Deux exemples d'apodisation : le fait d'adoucir
la transition au passage à zéro aux bords de la bande passante (a)
et c)) conduit à réduire l'amplitude des oscillations dans
le domaine spatial mais aussi à dégrader la résolution spatiale
(b) et d)).
|
Les facteurs de mérite
forment un ensemble de critères caractérisant le
comportement des fenêtres d'apodisation dans le domaine
spatial. Trois catégories
sont distinguées selon qu'ils quantifient des propriétés de
la fenêtre elle-même, du carré de son module ou du
logarithme de son module.
Ils caractérisent les propriétés de la fenêtre (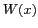 ) dans le domaine spatial (voir Fig. 5.4).
) dans le domaine spatial (voir Fig. 5.4).
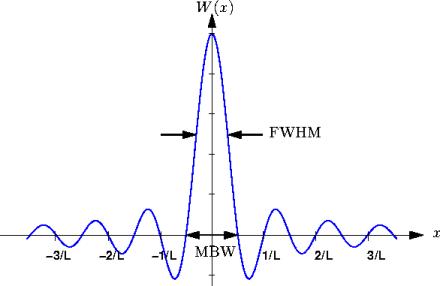
FWHM - Largeur à Mi-Hauteur
La largeur à mi-hauteur (noté FWHM pour
Full Width at Half-Maximum) est la largeur du lobe
principal de la fenêtre d'apodisation dans le domaine
spatial, généralement mesurée à -3 dB (par rapport au
maximum de la fonction).
La largeur du lobe principal (noté MBW pour Main Beam Width) est mesurée entre les deux
premiers zéros de chaque coté du lobe principal.
Ces deux facteurs de mérite caractérisent principalement la
résolution spatiale : plus leur valeur est faible, plus la
résolution spatiale est précise.
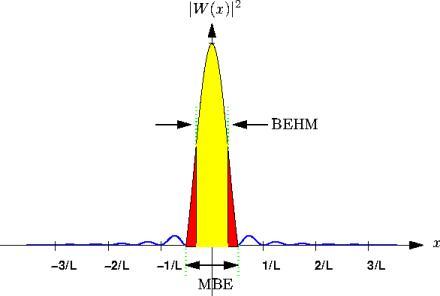
Ils caractérisent les propriétés du module au carré de la
fenêtre (
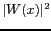 ) dans le domaine spatial (voir Fig. 5.5).
) dans le domaine spatial (voir Fig. 5.5).
L'efficacité du lobe principal (noté MBE pour
Main Beam Efficiency) est la quantité d'énergie
contenue dans le lobe principal, exprimée comme un
pourcentage de la quantité d'énergie totale contenue dans
tous les lobes.
L'efficacité à mi-hauteur du lobe principal (noté BEHM pour
Beam Efficiency at Half-Maximum) est elle-aussi
un pourcentage de la quantité d'énergie totale, mais calculée
à partir de la quantité d'énergie contenue à l'intérieur de
la largeur à mi-hauteur.
Ces deux facteurs donnent là encore une indication sur la
résolution spatiale mais aussi sur la sensibilité
radiométrique, puisque l'énergie dans les lobes secondaires
est prise en compte : plus leur énergie résiduelle est faible, plus les
fenêtres sont efficaces.
Figure 5.4: Facteurs de mérite linéaires : la largeur
à mi-hauteur du lobe principal est liée à la résolution
spatiale. L'axe des abscisses est gradué en unités de 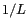 où
où 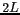 est la largeur de la bande passante.
est la largeur de la bande passante.
|
|
Figure 5.5: Facteurs de mérite quadratiques : l'efficacité
du lobe principal et son efficacité à mi-hauteur sont liées
à l'efficacité de la fenêtre.
|
|
Ils caractérisent les propriétés du logarithme du module de la
fenêtre (
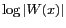 ) dans le domaine spatial (voir Fig. 5.6).
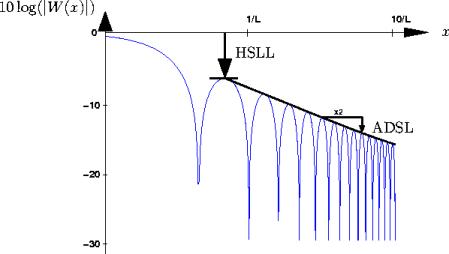
HSLL - plus grande amplitude des lobe secondairesLa plus grande amplitude des
lobes secondaires (HSLL pour Highest Side-Lobe Level), exprimée en
dB (par rapport au lobe principal) est lié de près à la fuite radiométrique
dans les premiers lobes secondaires : plus sa valeur est faible, plus la fuite
radiométrique est faible dans les lobes secondaires les plus proches du lobe
principal. La décroissance asymptotique des lobes secondaires Harris (notée
ADSL pour Asymptotic Decay of Side-Lobes) est la pente de la droite joignant
les maximum des lobes secondaires (en dB par octave) : plus sa valeur est faible,
plus la fuite radiométrique est faible dans les lobes secondaires les plus
éloignés du lobe principal.
) dans le domaine spatial (voir Fig. 5.6).
HSLL - plus grande amplitude des lobe secondairesLa plus grande amplitude des
lobes secondaires (HSLL pour Highest Side-Lobe Level), exprimée en
dB (par rapport au lobe principal) est lié de près à la fuite radiométrique
dans les premiers lobes secondaires : plus sa valeur est faible, plus la fuite
radiométrique est faible dans les lobes secondaires les plus proches du lobe
principal. La décroissance asymptotique des lobes secondaires Harris (notée
ADSL pour Asymptotic Decay of Side-Lobes) est la pente de la droite joignant
les maximum des lobes secondaires (en dB par octave) : plus sa valeur est faible,
plus la fuite radiométrique est faible dans les lobes secondaires les plus
éloignés du lobe principal.
Or, puisque l'amélioration de la sensibilité
radiométrique entraîne obligatoirement une dégradation de la
résolution spatiale, la variation, par exemple, de la largeur à
mi-hauteur en fonction du HSLL pour l'ensemble des fonctions d'apodisation
est monotone. Un nouveau facteur de mérite, adapté à
l'observation de distributions de  sur la Terre, a ainsi
été développé, de façon à pouvoir procéder à un choix
objectif d'une fenêtre d'apodisation optimale.
sur la Terre, a ainsi
été développé, de façon à pouvoir procéder à un choix
objectif d'une fenêtre d'apodisation optimale.
Anterrieu et al. EricApod ont introduit un
nouveau facteur de mérite, spécifiquement développé pour la
caractérisation des fenêtres d'apodisation dans un
contexte de télédétection de la surface terrestre. La distance
de plus courte approche (SACR, Side Area
Contribution Radius) est la distance, mesurée depuis une
marche entre deux températures initialement constantes
(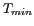 et
et 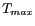 ), au delà de laquelle la
l'énergie contenue dans les oscillations est inférieure
à un pourcentage fixé de la différence
), au delà de laquelle la
l'énergie contenue dans les oscillations est inférieure
à un pourcentage fixé de la différence
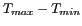 .
.
Cette marche est rencontrée dès lors que la scène observée
contient une forte discontinuité comme une ligne de
côte. La valeur fixée pour le pourcentage peut être adaptée
aux spécifications instrumentales en terme de résolution
spatiale et de fuite radiométrique. Plus le SACR est faible,
plus se réduit la taille de la région dans laquelle la fuite
radiométrique est significative. Il caractérise donc la
contamination, par les lobes secondaires, d'une région
proche d'une zone ayant des caractéristiques géophysiques différentes.
Figure 5.6: Facteurs de mérite logarithmiques : la plus
grande amplitude des lobes secondaires et la décroissance asymptotique
des lobes secondaires sont liées à la sensibilité radiométrique.
|
|
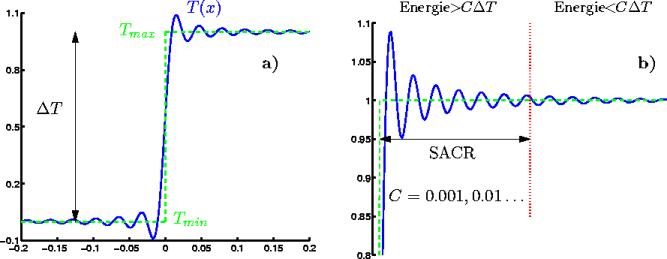
Figure 5.7: Distance de plus courte approche. a) le
SACR est utile lorsque la scène observée contient un saut (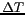 ) entre deux températures de brillance (
) entre deux températures de brillance (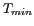 et
et 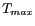 ) comme le long de lignes de côtes. b) un
zoom autour de
) comme le long de lignes de côtes. b) un
zoom autour de 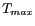 : le SACR est la distance mesurée à partir de la
mi-hauteur de la marche jusqu'à la ligne pointillée délimitant
deux régions.
: le SACR est la distance mesurée à partir de la
mi-hauteur de la marche jusqu'à la ligne pointillée délimitant
deux régions.
|
|




Next: 5.2 Les fenêtres d'apodisation
Up: 5. Apodisation
Previous: 5. Apodisation
nous
2005-03-31
![]() avec la distribution reconstruite
avec la distribution reconstruite ![]() . La première de ces deux sources de dégradation de la
qualité de la reconstruction est due aux oscillations que l'on observe
aux bords des créneaux (voir Fig. 5.2-a) : alors que
la température observée a une valeur constante, la température
reconstruite comporte des variations de l'ordre de 10% autour d'une valeur moyenne.
D'autre part, la dégradation de la résolution spatiale apparaît
clairement dans la difficulté à localiser précisément les
limites du créneau reconstruit (voir Fig. 5.2-b).
. La première de ces deux sources de dégradation de la
qualité de la reconstruction est due aux oscillations que l'on observe
aux bords des créneaux (voir Fig. 5.2-a) : alors que
la température observée a une valeur constante, la température
reconstruite comporte des variations de l'ordre de 10% autour d'une valeur moyenne.
D'autre part, la dégradation de la résolution spatiale apparaît
clairement dans la difficulté à localiser précisément les
limites du créneau reconstruit (voir Fig. 5.2-b).



![]() et
et ![]() ), au delà de laquelle la
l'énergie contenue dans les oscillations est inférieure
à un pourcentage fixé de la différence
), au delà de laquelle la
l'énergie contenue dans les oscillations est inférieure
à un pourcentage fixé de la différence
![]() .
.