Les fenêtres d'apodisation 2D peuvent être directement adaptées des
traditionnelles fenêtres
1D Harris Yavuz Filler Norton Nuttall
: pour chaque point ![]() de la bande passante de
l'instrument, la
valeur de la fenêtre 2D dépend de la variable radiale
normalisée
de la bande passante de
l'instrument, la
valeur de la fenêtre 2D dépend de la variable radiale
normalisée
![]() , avec
, avec
![]() et
et
![]() Lannesproc. La
fonction
Lannesproc. La
fonction
![]() ainsi construite est
centro-symétrique dans le domaine de FOURIER et
son support à la forme de la bande passante. Dans le domaine
spatial, la fenêtre est notée
ainsi construite est
centro-symétrique dans le domaine de FOURIER et
son support à la forme de la bande passante. Dans le domaine
spatial, la fenêtre est notée
![]() et elle
présente une symétrie liée à la forme de la bande passante.
et elle
présente une symétrie liée à la forme de la bande passante.
Anterrieu et al. EricApod ont étudié les caractéristiques
de plus de 20 fenêtres 2D définies sur un maillage hexagonal (voir
Tab. 5.1) et pour un instrument en Y comportant
27 antennes par bras et un espace entre les antennes
![]() . Parmi les fenêtres étudiées, certaines
dépendent d'un paramètre et forment alors une famille de fenêtres
(CAUCHY, POISSON, ..., KAISER,
VAN DER MASS). Le tableau 5.2
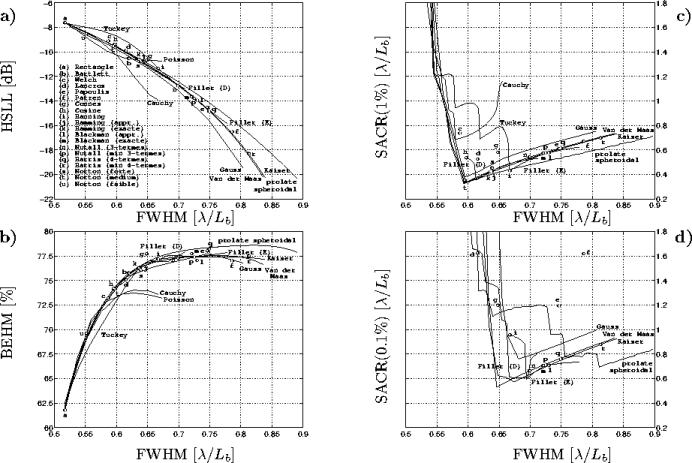
et la figure 5.9 reprennent les principaux résultats.
Pour les familles de fenêtres, les facteurs de mérite sont calculés
pour la plus petite et la plus grande des valeurs du paramètre ainsi que
pour les valeurs optimales du point de vue du SACR.
. Parmi les fenêtres étudiées, certaines
dépendent d'un paramètre et forment alors une famille de fenêtres
(CAUCHY, POISSON, ..., KAISER,
VAN DER MASS). Le tableau 5.2
et la figure 5.9 reprennent les principaux résultats.
Pour les familles de fenêtres, les facteurs de mérite sont calculés
pour la plus petite et la plus grande des valeurs du paramètre ainsi que
pour les valeurs optimales du point de vue du SACR.
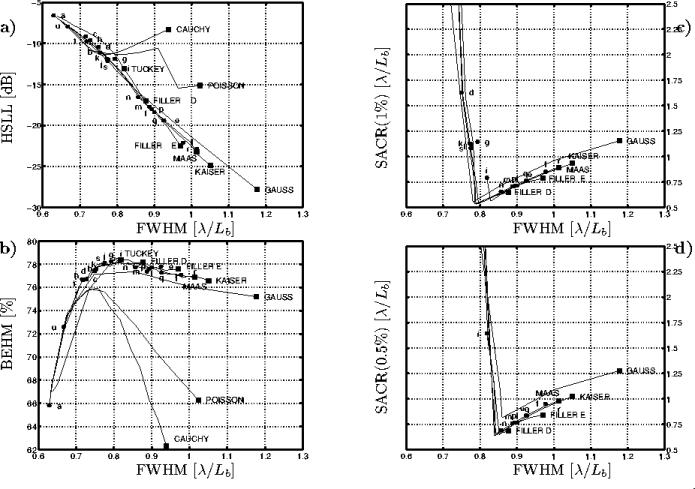
J'ai complété ces travaux en caractérisant ces mêmes fenêtres pour une configuration instrumentale en U et un maillage cartésien. Le tableau 5.3 et la figure 5.10 reprennent les principaux résultats.
Afin de faciliter la comparaison et étant donné que les
propriétés des fenêtres d'apodisation dépendent
naturellement des dimensions de l'instrument, les fréquences
spatiales angulaires sont exprimées en unités de
![]() où
où ![]() est la longueur d'onde d'observation et
est la longueur d'onde d'observation et ![]() la
longueur de chaque bras et les facteurs de mérite sont
donnés en unités de
la
longueur de chaque bras et les facteurs de mérite sont
donnés en unités de
![]() .
.
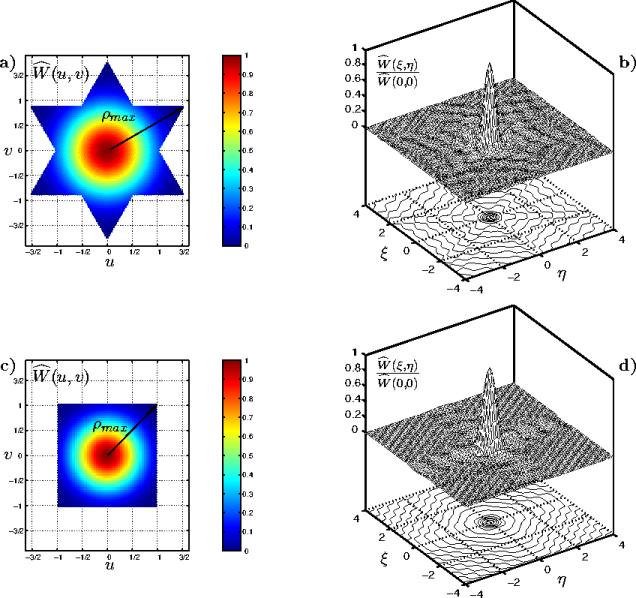
Les figures 5.8-a, b, c et d illustrent les valeurs prises par la fenêtre de BLACKMAN (approchée) dans le domaine de FOURIER (a et c) et dans le domaine spatial (b et d) pour une configuration en Y (a et b) et une configuration en U (c et d). Les contours tracés sous les fenêtres dans le domaine spatial permettent d'apprécier la répartition des maxima des lobes secondaires selon les axes de symétrie des bandes passantes correspondantes.
En comparant les caractéristiques des fenêtres pour les deux géométries étudiées, deux propriétés émergent : les fenêtres d'apodisation pour une configuration en Y sont plus étroites que pour une configuration en U, alors que les lobes secondaires sont plus élevés. En effet, à nombre d'antennes par bras et espace inter-antenne égaux, une configuration en Y possède une meilleure résolution spatiale (FWHM) mais une moins bonne sensibilité radiométrique (HSLL) qu'une configuration en U.
Les différences observées sur le FWHM s'expliquent en observant
que la plus grande distance entre deux antennes d'un instrument en Y vaut
![]() , ce qui est supérieur à la plus grande distance
entre deux antennes d'un instrument en U,
, ce qui est supérieur à la plus grande distance
entre deux antennes d'un instrument en U,
![]() . Ainsi, comme le montrent
les figures 5.8-a et 5.8-c, pour une
même longueur
. Ainsi, comme le montrent
les figures 5.8-a et 5.8-c, pour une
même longueur ![]() ,
, ![]() , la bande passante en étoile est plus étendue que la bande
passante rectangulaire.
, la bande passante en étoile est plus étendue que la bande
passante rectangulaire.
|
D'autre part, le classement des fenêtres en termes de FWHM, HSLL ou BEHM n'est pas modifié par la configuration de l'instrument. Par exemple, parmi les fenêtres ne dépendant pas d'un paramètre, PARZEN, LANCZOS NUTALL min 3-termes et HARRIS min 4-termes possèdent le lobe central le plus large et une hauteur des lobes secondaires la plus faibles, et ce dans les deux cas. Parmi les familles de fenêtres, GAUSS, KAISER et MASS ont leur lobe principal de plus en plus large et une hauteur des lobes de plus en plus faible au fur et à mesure que la valeur du paramètre dont elles dépendent augmente. Citons toutefois FILLER exacte qui semble avoir un meilleur comportement comparé à MASS pour une configuration en U, ce qui n'est pas le cas pour une configuration en Y.
Comme on l'a vu précédemment, le SACR a été élaboré de manière à permettre un choix objectif parmi l'ensemble des fenêtres disponibles. Notons préalablement que, pour une configuration en U, le SACR n'offrait pas de résultats probants pour un seuil de 0.1% (seul un petit nombre de fenêtre remplissait ce critère), les résultats présentés dans la figure 5.10 et le tableau 5.3 correspondent à un seuil de 0.5%. Les fenêtres les plus performantes, quelque soit la configuration de l'instrument, sont les familles de fenêtres, à condition de choisir la valeur optimale pour leur paramètre. Cette valeur est différente selon le seuil choisi pour le calcul du SACR et la configuration de l'instrument.
Toutefois, alors que la fenêtre de
MASS est optimale du point de vue du SACR pour une
géométrie en Y, c'est la fenêtre de FILLER D
qui est la plus performante pour une configuration en U.
En conclusion, les caractéristiques des fenêtres
d'apodisation changent avec la configuration du réseau
interférométrique. Une géométrie en Y conduit à une meilleure
résolution radiométrique alors qu'une géométrie en U permet
d'atteindre une meilleure sensibilité radiométrique. J'ai
aussi montré que les fenêtres les plus performantes du point
de vue du SACR changent selon cette configuration. Selon ce
critère et pour un seuil de 1%, dans le cas d'une
configuration en U, la fenêtre de
FILLER D calculée pour un paramètre
![]() permet un compromis optimal entre la
résolution spatiale et la sensibilité radiométrique.
permet un compromis optimal entre la
résolution spatiale et la sensibilité radiométrique.
Ces résultats ont été établis pour des fenêtres possédant
une symétrie circulaire alors que les bandes passantes ont
une anisotropie propre à la géométrie de l'instrument. Par
la suite, j'ai donc modifié le calcul de la variable
![]() afin de
tenir compte de cette anisotropie et ainsi
améliorer la sensibilité radiométrique des fenêtres.
afin de
tenir compte de cette anisotropie et ainsi
améliorer la sensibilité radiométrique des fenêtres.
| Rectangle | |
| Bartlett |
|
| Welch |
|
| Lanczos |
|
| Papoulis |
|
| Parzen |
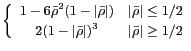
|
| Connes |
|
| Cosine |
|
| Hanning |
|
| Hamming |
|
| Hamming |
|
| Blackman |
|
| Blackman |
|
| Nutall |
|
| Nutall |
|
| Harris |
|
| Harris |
|
| Norton-Beer |
|
| Norton-Beer |
|
| Norton-Beer |
|
| Cauchy |
|
| Poisson |
e |
| Gauss |
e |
| Filler (D) |
|
| Filler (E) |
|
| Tuckey |
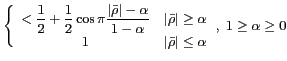
|
| Kaiser |
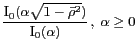
|
| Van der Maas |
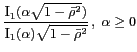
|
DIV ALIGN="CENTER">
|
|
| FWHM | HSLL | BEHM | SACR(1%) | SACR(0.1%) | ||
|
|
[
|
[dB] | [%] | [
|
[
|
|
| Rectangle | 0.517 | -7.626 | 61.79 | |||
| Bartlett | 0.620 | -10.524 | 75.77 | 3.161 | ||
| Welch | 0.587 | -9.110 | 73.23 | 0.737 | 2.491 | |
| Lanczos | 0.615 | -9.898 | 75.09 | 0.526 | 1.624 | |
| Papoulis | 0.746 | -14.542 | 78.03 | 0.609 | 1.194 | |
| Parzen | 0.786 | -16.520 | 77.02 | 0.673 | 1.620 | |
| Connes | 0.648 | -10.684 | 77.73 | 0.581 | 1.198 | |
| Cosine | 0.597 | -9.377 | 74.17 | 0.536 | 2.184 | |
| Hanning | 0.667 | -11.339 | 77.17 | 0.431 | 0.957 | |
| Hamming |
0.638 | -10.663 | 76.16 | 0.425 | ||
| Hamming |
0.636 | -10.609 | 76.31 | 0.424 | ||
| Blackman |
0.730 | -13.940 | 77.06 | 0.577 | 0.709 | |
| Blackman |
0.721 | -13.644 | 77.75 | 0.575 | 0.706 | |
| Nutall |
0.699 | -12.779 | 77.29 | 0.542 | 0.666 | |
| Nutall |
0.725 | -13.796 | 77.40 | 0.578 | 0.710 | |
| Harris |
0.749 | -14.852 | 78.23 | 0.614 | 0.759 | |
| Harris |
0.813 | -18.304 | 77.50 | 0.698 | 0.878 | |
| Norton-Beer |
0.639 | -10.782 | 76.05 | 0.453 | ||
| Norton-Beer |
0.595 | -9.535 | 74.21 | 0.352 | ||
| Norton-Beer |
0.552 | -8.522 | 69.61 | 2.014 | ||
| Cauchy 1.0 | 0.548 | -8.459 | 68.92 | 1.219 | ||
|
1.53 |
0.578 | -9.397 | 70.92 | 0.686 | ||
|
|
0.653 | -13.785 | 74.03 | 1.160 | ||
| Poisson 1.0 | 0.559 | -9.043 | 70.92 | |||
|
|
0.673 | -10.733 | 73.14 | |||
| Gauss 1.0 | 0.559 | -8.656 | 71.13 | 1.052 | ||
|
1.22 |
0.582 | -9.582 | 72.22 | 0.316 | ||
|
1.84 |
0.670 | -11.985 | 76.40 | 0.555 | 0.749 | |
|
|
0.804 | -19.505 | 76.81 | 0.752 | 0.994 | |
| Filler (D) 0.0 | 0.597 | -9.377 | 74.17 | 0.536 | 2.184 | |
|
0.06 |
0.613 | -9.919 | 75.21 | 0.355 | 1.651 | |
|
0.27 |
0.695 | -12.533 | 77.68 | 0.518 | 0.608 | |
|
|
0.711 | -13.036 | 77.96 | 0.530 | 0.804 | |
| Filler (E) 0.0 | 0.667 | -11.339 | 77.17 | 0.431 | 0.957 | |
|
0.09 |
0.694 | -12.442 | 77.97 | 0.508 | 0.593 | |
|
|
0.778 | -15.852 | 77.82 | 0.623 | 0.736 | |
| Kaiser 1.0 | 0.527 | -7.844 | 64.16 | 3.174 | ||
|
3.47 |
0.592 | -9.388 | 74.39 | 0.322 | ||
|
6.01 |
0.661 | -11.393 | 77.47 | 0.464 | 0.539 | |
|
|
0.839 | -20.270 | 76.99 | 0.731 | 0.925 | |
| Van der Maas 1.0 | 0.522 | -7.739 | 63.68 | 4.301 | ||
|
4.16 |
0.585 | -9.244 | 73.38 | 0.311 | ||
|
6.43 |
0.644 | -10.913 | 76.76 | 0.444 | 0.521 | |
|
|
0.812 | -18.416 | 77.47 | 0.703 | 0.888 |
| FWHM | HSLL | BEHM | SACR(1%) | SACR(0.5%) | ||
|
|
[
|
[dB] | [%] | [
|
[
|
|
| Rectangle | 0.629 | -6.604 | 65.80 | |||
| Bartlett | 0.754 | -11.126 | 77.63 | |||
| Welch | 0.716 | -9.138 | 76.72 | |||
| Lanczos | 0.750 | -10.443 | 77.43 | 1.629 | ||
| Papoulis | 0.924 | -19.388 | 77.82 | 0.761 | 0.839 | |
| Parzen | 0.977 | -22.101 | 77.09 | 0.852 | 0.952 | |
| Connes | 0.793 | -11.894 | 78.25 | 1.146 | ||
| Cosine | 0.728 | -9.577 | 76.73 | |||
| Hanning | 0.819 | -13.087 | 78.41 | 0.792 | 1.641 | |
| Hamming |
0.776 | -11.947 | 78.11 | 1.117 | ||
| Hamming |
0.772 | -11.853 | 78.02 | 1.129 | ||
| Blackman |
0.900 | -18.411 | 77.75 | 0.713 | 0.766 | |
| Blackman |
0.888 | -17.759 | 77.39 | 0.704 | 0.757 | |
| Nutall |
0.857 | -16.566 | 77.74 | 0.652 | 0.694 | |
| Nutall |
0.893 | -18.029 | 77.61 | 0.711 | 0.765 | |
| Harris |
0.926 | -19.380 | 77.29 | 0.765 | 0.833 | |
| Harris |
1.015 | -22.875 | 76.90 | 0.887 | 0.975 | |
| Norton-Beer |
0.775 | -12.148 | 78.05 | 1.082 | ||
| Norton-Beer |
0.718 | -9.768 | 76.65 | |||
| Norton-Beer |
0.667 | -7.926 | 72.59 | |||
| Cauchy 0.5 | 0.640 | -6.947 | 68.23 | |||
|
|
0.939 | -8.287 | 62.34 | |||
| Poisson 0.5 | 0.652 | -7.429 | 69.89 | |||
|
|
1.023 | -15.129 | 66.28 | |||
| Gauss 0.5 | 0.641 | -6.977 | 68.32 | |||
|
1.68 |
0.781 | -12.604 | 77.64 | 0.554 | ||
|
2.02 |
0.860 | -16.019 | 77.29 | 0.724 | 0.816 | |
|
|
1.177 | -27.822 | 75.20 | 1.155 | 1.278 | |
| Filler (D) 0.0 | 0.728 | -9.577 | 76.73 | |||
|
0.16 |
0.786 | -12.376 | 78.07 | 0.533 | ||
|
0.25 |
0.839 | -15.127 | 78.02 | 0.613 | 0.644 | |
|
|
0.877 | -16.980 | 78.20 | 0.651 | 0.687 | |
| Filler (E) 0.0 | 0.819 | -13.09 | 78.41 | 0.792 | 1.641 | |
|
0.03 |
0.829 | -13.766 | 78.10 | 0.561 | 1.574 | |
|
0.09 |
0.852 | -15.394 | 78.22 | 0.620 | 0.651 | |
|
|
0.970 | -22.454 | 77.60 | 0.786 | 0.844 | |
| Tuckey 0.0 | 0.819 | -13.087 | 78.41 | 0.792 | 1.641 | |
|
|
0.638 | -6.689 | 67.03 | |||
| Kaiser 0.5 | 0.632 | -6.6.692 | 66.57 | |||
|
5.69 |
0.796 | -12.743 | 77.87 | 0.537 | ||
|
6.99 |
0.842 | -15.227 | 78.06 | 0.615 | 0.646 | |
|
|
1.051 | -24.878 | 76.59 | 0.932 | 1.024 | |
| Van der Maas 0.5 | 0.630 | -6.648 | 65.969 | |||
|
6.56 |
0.789 | -12.522 | 77.82 | 0.533 | ||
|
8.08 |
0.842 | -15.457 | 77.99 | 0.624 | 0.657 | |
|
|
1.014 | -23.256 | 76.888 | 0.894 | 0.984 |