Jusqu'à présent, les fenêtres d'apodisation sont des
fonctions bidimensionnelles de la variable radiale
![]() , où
, où ![]() est
la distance
est
la distance
![]() mesurée depuis la fréquence
nulle à l'intérieur de la bande passante, et où
mesurée depuis la fréquence
nulle à l'intérieur de la bande passante, et où
![]() est égal à la plus grande de ces
distances. Ainsi, il subsiste des valeurs non nulles aux
bords de la bande passante dans le domaine de Fourier,
autour des creux de l'étoile
pour une configuration en Y ou au centre des cotés du
rectangle pour une configuration en U. Ces valeurs non
nulles vont se traduire par une plus grande amplitude des
oscillations de Gibbs dans le domaine spatial. En
modifiant l'expression de
est égal à la plus grande de ces
distances. Ainsi, il subsiste des valeurs non nulles aux
bords de la bande passante dans le domaine de Fourier,
autour des creux de l'étoile
pour une configuration en Y ou au centre des cotés du
rectangle pour une configuration en U. Ces valeurs non
nulles vont se traduire par une plus grande amplitude des
oscillations de Gibbs dans le domaine spatial. En
modifiant l'expression de
![]() , il est possible
d'adapter la forme des fenêtres à la forme des bandes
passantes et ainsi de réduire les valeurs non nulles
subsistant sur leurs bords, diminuant au final l'amplitude
des oscillations de Gibbs BPApod.
, il est possible
d'adapter la forme des fenêtres à la forme des bandes
passantes et ainsi de réduire les valeurs non nulles
subsistant sur leurs bords, diminuant au final l'amplitude
des oscillations de Gibbs BPApod.
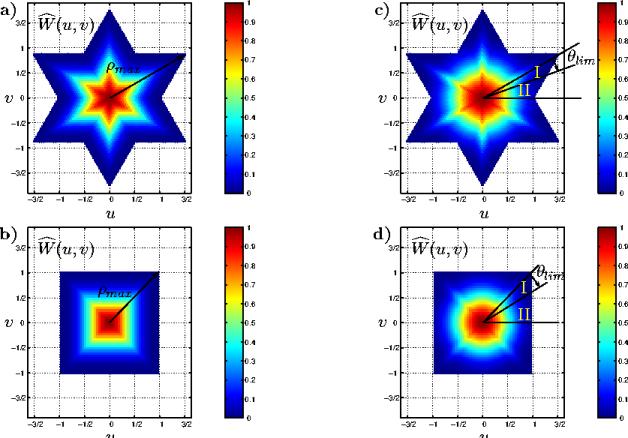
L'introduction d'une dépendance angulaire dans le calcul de
![]() permet d'adapter complètement la forme de la fenêtre
à la forme de la bande passante (voir Fig. 5.11-a,-c).
Il est pour cela nécessaire de calculer, pour chaque point
permet d'adapter complètement la forme de la fenêtre
à la forme de la bande passante (voir Fig. 5.11-a,-c).
Il est pour cela nécessaire de calculer, pour chaque point ![]() de la bande passante, la longueur
de la bande passante, la longueur
![]() du segment joignant la fréquence nulle, la
fréquence
du segment joignant la fréquence nulle, la
fréquence ![]() le bord de
le bord de ![]() . Cette longueur est paramétrée par l'angle
. Cette longueur est paramétrée par l'angle ![]() mesuré depuis l'axe liant la fréquence nulle à
la fréquence la plus grande de la bande passante (une pointe de l'étoile
ou un sommet du rectangle). Etant données les symétries des bandes
passante, pour une configuration en Y,
mesuré depuis l'axe liant la fréquence nulle à
la fréquence la plus grande de la bande passante (une pointe de l'étoile
ou un sommet du rectangle). Etant données les symétries des bandes
passante, pour une configuration en Y, ![]() varie dans l'intervalle
varie dans l'intervalle
![]() et
et
![]() s'exprime ainsi :
s'exprime ainsi :
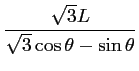 |
(5.1) |
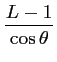 |
(5.2) | ||
![$\displaystyle [0^\circ ~\left(\arctan \frac{\displaystyle L}{\displaystyle L-1}\right)\pi/180~^\circ ]$](img833.gif) |
Il est alors possible de circonscrire l'adaptation de la forme de la fenêtre
à la forme de la bande passante à l'intérieur d'une région
donnée, délimitée par la valeur d'un angle limite
![]() (voir Fig. 5.11-b,-d). Ainsi, pour
chaque point de la bande passante, la distance
(voir Fig. 5.11-b,-d). Ainsi, pour
chaque point de la bande passante, la distance
![]() est paramétrée par l'angle
est paramétrée par l'angle ![]() correspondant :
correspondant :
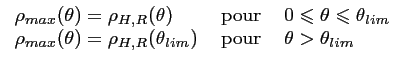 |
(5.3) |
Lorsque
![]() est nul, on retrouve le cas d'une
symétrie circulaire avec
est nul, on retrouve le cas d'une
symétrie circulaire avec
![]() constant. Lorsque
constant. Lorsque
![]() ou
ou
![]() , la forme de la fenêtre d'apodisation
colle parfaitement à la forme en étoile de la bande passante.
, la forme de la fenêtre d'apodisation
colle parfaitement à la forme en étoile de la bande passante.
|
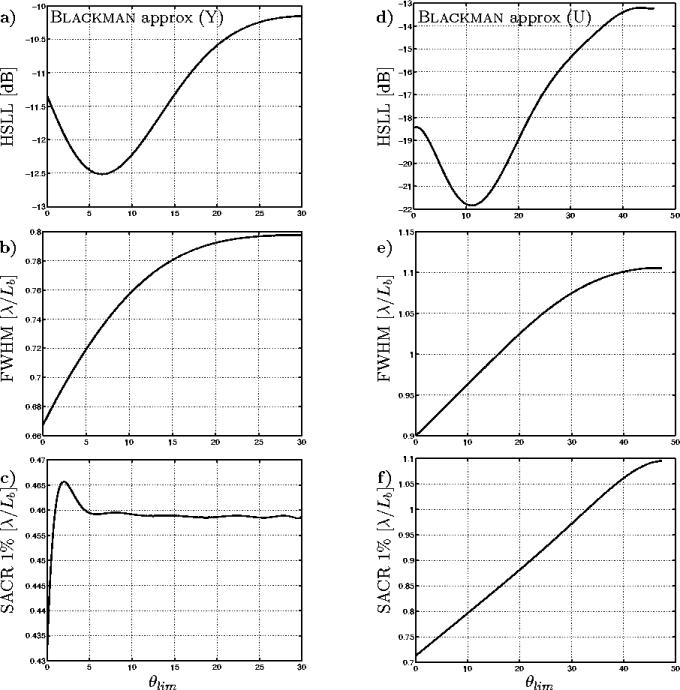
La valeur des lobes secondaires pour une fenêtre donnée est conditionnée par de multiples caractéristiques dont les valeurs qu'elle prend au bord de la bande passante, bien entendu, mais aussi l'allure de la décroissance depuis la fréquence nulle. Il est donc difficile de prévoir la valeur de cet angle optimal, qui est différent pour chacune des fenêtre, mais l'on peut avancer quelques hypothèse pour expliquer son existence.
La décroissance de la hauteur des lobes est due à
une diminution de la valeur de la fenêtre au bord de la bande
passante dans la zone I. Cependant, l'adaptation de forme
fait aussi apparaître un angle aigu le long de l'axe de
symétrie orienté vers la pointe de
l'étoile (
![]() ): cette arête va augmenter la hauteur des lobes
secondaires au delà même de la valeur initiale. Pour les faibles valeurs de
): cette arête va augmenter la hauteur des lobes
secondaires au delà même de la valeur initiale. Pour les faibles valeurs de
![]() , la
diminution des valeurs au bord de la bande passante dans la zone I l'emporte sur
l'apparition cette arête dans la zone II, l'effet s'inversant par la
suite, d'où l'existence d'un angle optimal.
, la
diminution des valeurs au bord de la bande passante dans la zone I l'emporte sur
l'apparition cette arête dans la zone II, l'effet s'inversant par la
suite, d'où l'existence d'un angle optimal.
|
Puisque la zone sensible du point de vue de la hauteur des lobes secondaires
est liée à la présence d'un angle aigu le long de l'axe de symétrie
dirigé vers la pointe de l'étoile, il a été envisagé
d'introduire une dépendance radiale dans le calcul de
![]() , en plus de la dépendance angulaire. Ainsi, il sera
possible de restreindre l'adaptation de forme de la fenêtre aux fréquences
situées à une distance
, en plus de la dépendance angulaire. Ainsi, il sera
possible de restreindre l'adaptation de forme de la fenêtre aux fréquences
situées à une distance ![]() au delà d'un rayon limite
au delà d'un rayon limite
![]() (voir Fig. 5.13). Pour chaque point
de la bande passante, la distance
(voir Fig. 5.13). Pour chaque point
de la bande passante, la distance
![]() est paramétrée par l'angle
est paramétrée par l'angle ![]() et la distance
et la distance ![]() correspondant :
correspondant :
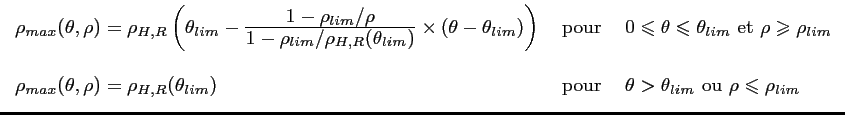 |
(5.4) |
|
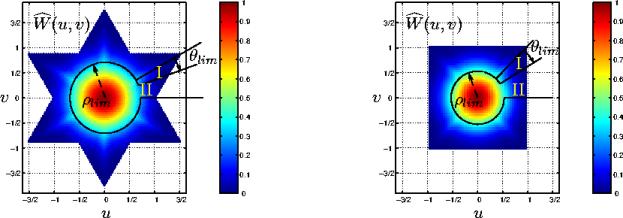
En configuration U, le gain sur le HSLL ne compense pas la perte sur le FWHM,
même si la distance de plus courte approche diminue avec
![]() croissant, elle reste supérieure au cas initial 5.14.
croissant, elle reste supérieure au cas initial 5.14.
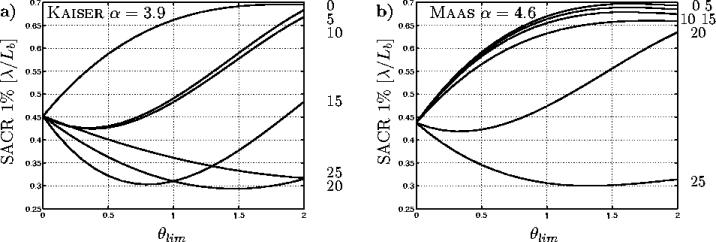
En configuration Y, cela reste vrai pour les fenêtres simples , ne dépendant pas d'un paramètre, mais on observe une légère amélioration du SACR pour les familles de fenêtres et notamment pour KAISER et MASS. <
|
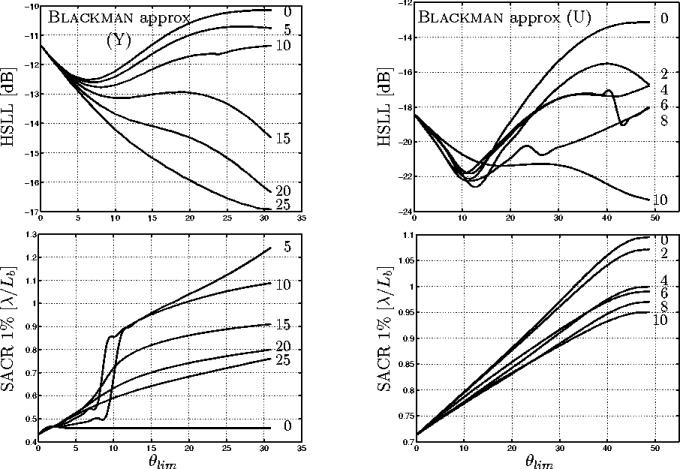
Là encore, il est difficile de trouver une seule explication
à la présence de ce minimum. On peut toutefois remarquer que
les familles de fenêtres FILLER, KAISER et
MAAS, de part la présence d'un paramètre ![]() modifiant finement l'allure de la décroissance entre la
fréquence nulle et le bord de la bande passante,
sont déjà les familles les plus performante du point de vue
du SACR. La combinaison de l'action de
modifiant finement l'allure de la décroissance entre la
fréquence nulle et le bord de la bande passante,
sont déjà les familles les plus performante du point de vue
du SACR. La combinaison de l'action de ![]() et de
l'introduction d'une dépendance angulaire et radiale sur
et de
l'introduction d'une dépendance angulaire et radiale sur
![]() , autorise une souplesse dans la déformation de
de ces fenêtres que n'ont pas les fenêtres simple ,
et permet de diminuer la hauteur des lobes
secondaires tout en maintenant la dégradation de la largeur
du lobe principal sous contrôle.
, autorise une souplesse dans la déformation de
de ces fenêtres que n'ont pas les fenêtres simple ,
et permet de diminuer la hauteur des lobes
secondaires tout en maintenant la dégradation de la largeur
du lobe principal sous contrôle.
Le tableau 5.4 donne pour KAISER
et MAAS, le triplet
![]() et la valeur améliorée correspondante
pour le SACR 1%, constituant les meilleurs performances pour l'ensemble des
fenêtres.
et la valeur améliorée correspondante
pour le SACR 1%, constituant les meilleurs performances pour l'ensemble des
fenêtres.
|
En conclusion, le bilan de ce travail sur l'adaptation de la
forme de la fenêtre est partagé. Si la déformation des
fenêtres permet effectivement d'améliorer la hauteur des
lobes secondaires, et par là même la sensibilité
radiométrique, la largeur du lobe principal est augmentée,
dégradant la résolution spatiale. Toutefois, pour une
configuration en Y, il existe un triplet
(
![]() ) pour lequel le SACR est
légèrement amélioré. Sans doute le principal avantage de
cette paramétrisation des fenêtres d'apodisation est-il de
donner la possibilité de faire varier finement le compromis
entre hauteur des lobes secondaires et largeur du lobe
principal, permettant ainsi à un utilisateur de trouver
l'adaptation de forme qui lui convient compte tenu de ses
objectifs et des contraintes sur l'estimation des paramètres
géophysiques.
) pour lequel le SACR est
légèrement amélioré. Sans doute le principal avantage de
cette paramétrisation des fenêtres d'apodisation est-il de
donner la possibilité de faire varier finement le compromis
entre hauteur des lobes secondaires et largeur du lobe
principal, permettant ainsi à un utilisateur de trouver
l'adaptation de forme qui lui convient compte tenu de ses
objectifs et des contraintes sur l'estimation des paramètres
géophysiques.
Biographie(s)
