



Next: Partie III
Up: 6. Passage au repère
Previous: 6.2 Rééchantillonnage des champs
La famille de fenêtre de KAISER Kaiser a
été sélectionnée pour être à la base de la construction des
fenêtres qui seront appliquées à chaque pixel du champ
reconstruit :
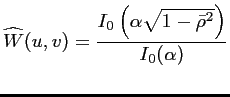 |
(6.30) |
où 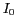 est la fonction de BESSEL modifiée d'ordre 0,
est la fonction de BESSEL modifiée d'ordre 0,
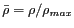 et
et 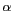 est un réel positif (pour
est un réel positif (pour 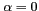 , on obtient une fenêtre rectangle). La valeur de ce
paramètre modifie la décroissance de la fenêtre
, on obtient une fenêtre rectangle). La valeur de ce
paramètre modifie la décroissance de la fenêtre
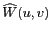 depuis la fréquence nulle jusqu'au bord de la
bande passante, modifiant ainsi les caractéristiques de
depuis la fréquence nulle jusqu'au bord de la
bande passante, modifiant ainsi les caractéristiques de
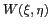 dans le repère des antennes. Pour un pixel
dans le repère des antennes. Pour un pixel
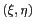 et un paramètre
et un paramètre 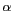 donné, la fonction de transfert est à symétrie
circulaire dans le repère des cosinus directeurs et elliptique le repère
terrestre (voir Fig. 6.10).
donné, la fonction de transfert est à symétrie
circulaire dans le repère des cosinus directeurs et elliptique le repère
terrestre (voir Fig. 6.10).
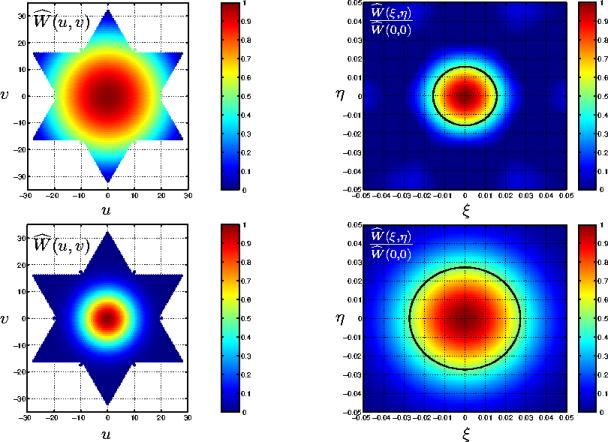
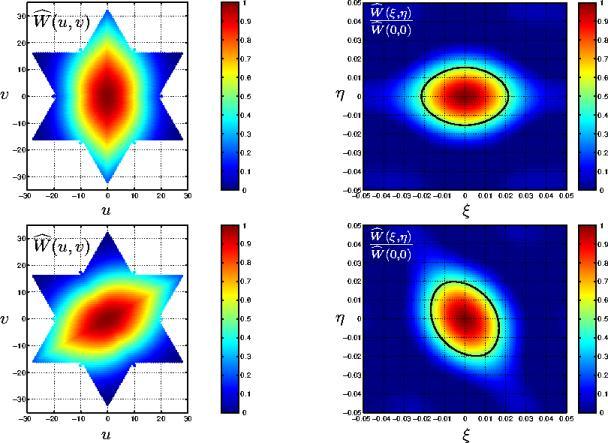
Figure 6.10: La fenêtre de KAISER pour
deux valeurs du paramètre 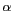 . A gauche, la fenêtre a une symétrie circulaire
dans le domaine de FOURIER mais, à droite,
une symétrie elliptique dans le domaine spatial (l'ellipse trace le contour
à -3dB).
. A gauche, la fenêtre a une symétrie circulaire
dans le domaine de FOURIER mais, à droite,
une symétrie elliptique dans le domaine spatial (l'ellipse trace le contour
à -3dB).
|
L'idée
sous-jacente au multi-fenêtrage est d'appliquer une
fenêtre d'apodisation propre à chaque pixel
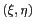 (sur une grille régulière dans le repère terrestre) pour
obtenir une résolution isotrope dans le champ reconstruit
projeté sur Terre.
(sur une grille régulière dans le repère terrestre) pour
obtenir une résolution isotrope dans le champ reconstruit
projeté sur Terre.
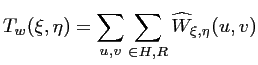 e e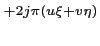 |
(6.31) |
Le paramètre 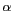 contrôlant la forme de la fenêtre, il
lui est ajouté une dépendance angulaire à l'intérieur de la
bande passante, de façon à rendre la fenêtre elliptique dans
le repère des cosinus directeurs, et donc, avec la bonne
inclinaison et la bonne ellipticité, à symétrie circulaire
dans le repère terrestre. Pour un pixel donné
contrôlant la forme de la fenêtre, il
lui est ajouté une dépendance angulaire à l'intérieur de la
bande passante, de façon à rendre la fenêtre elliptique dans
le repère des cosinus directeurs, et donc, avec la bonne
inclinaison et la bonne ellipticité, à symétrie circulaire
dans le repère terrestre. Pour un pixel donné
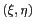 et pour chaque point
et pour chaque point
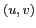 de la bande passante, le paramètre
de la bande passante, le paramètre 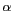 est
calculé à partir d'une simple relation linéaire :
est
calculé à partir d'une simple relation linéaire :
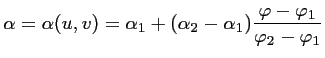 |
(6.32) |
où
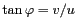 et
et 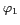 ,
,
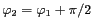 ,
, 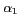 et
et 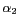 définis comme sur la figure 6.11.
Cette relation a été élaborée de façon à faire varier
définis comme sur la figure 6.11.
Cette relation a été élaborée de façon à faire varier
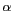 linéairement entre
linéairement entre 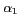 et
et 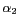 pour
pour
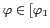
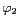 ] et à conserver la symétrie de la fenêtre
] et à conserver la symétrie de la fenêtre
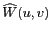 . La figure 6.12 montre
que les valeurs de ces 3 paramètres (
. La figure 6.12 montre
que les valeurs de ces 3 paramètres (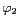 est lié à
est lié à 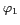 ) contrôlent bien l'ellipticité de la fenêtre
dans le domaine de FOURIER et donc dans le domaine spatial.
) contrôlent bien l'ellipticité de la fenêtre
dans le domaine de FOURIER et donc dans le domaine spatial.
Figure 6.11: Paramétrisation linéaire du paramètre
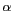 de la famille de fenêtre KAISER.
de la famille de fenêtre KAISER.
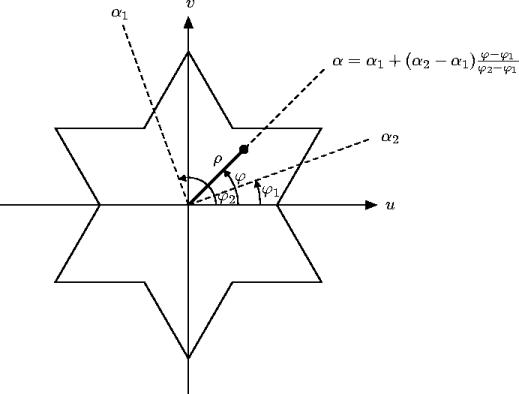
Figure 6.12: Illustration de la déformation de la fenêtre
de KAISER par la paramétrisation de 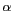 . La dépendance en
. La dépendance en 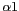 ,
, 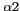 ,
, 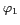 et
et 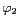 permet d'imprimer une symétrie elliptique à la
fenêtre dans le domaine de FOURIER et modifier ainsi
sa symétrie dans le domaine spatial.
permet d'imprimer une symétrie elliptique à la
fenêtre dans le domaine de FOURIER et modifier ainsi
sa symétrie dans le domaine spatial.
|
Reste à trouver les paramètres
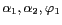 pour lesquels la fenêtre est à
symétrie circulaire sur la Terre. Pour une résolution donnée
pour lesquels la fenêtre est à
symétrie circulaire sur la Terre. Pour une résolution donnée
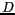 , après initialisation, un algorithme d'ajustement des paramètres d'une
ellipse fournit l'inclinaison
, après initialisation, un algorithme d'ajustement des paramètres d'une
ellipse fournit l'inclinaison 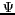 et l'ellipticité
et l'ellipticité 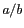 de la
fonction de transfert à -3dB dans le repère terrestre ellipse. Une
méthode d'optimisation non linéaire de type BFGS nous permet
de minimiser le critère :
de la
fonction de transfert à -3dB dans le repère terrestre ellipse. Une
méthode d'optimisation non linéaire de type BFGS nous permet
de minimiser le critère :
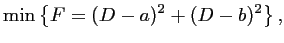 |
(6.33) |
et ainsi de trouver les paramètres
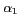 ,
, 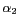 et
et 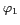 qui conduisent une résolution
isotrope pour
qui conduisent une résolution
isotrope pour 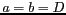 ,
, 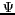 n'étant pas défini pour un
cercle.
n'étant pas défini pour un
cercle.
Bien entendu, la résolution 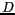 imposée ne peut être atteinte dans l'ensemble du champ
de vue reconstruit. La figure 6.15 montre comment le
multi-fenêtrage a été appliqué à la scène présentée
sur la figure 6.14 pour une résolution
imposée ne peut être atteinte dans l'ensemble du champ
de vue reconstruit. La figure 6.15 montre comment le
multi-fenêtrage a été appliqué à la scène présentée
sur la figure 6.14 pour une résolution
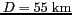 . L'effet est particulièrement probant le long
des côtes britanniques, la zone de transition entre les terres et la mer
s'élargissant nettement lorsque l'on s'éloigne du point sub-satellite
avec une apodisation classique, alors qu'elle est constante avec le multi-fenêtrage.
La contrepartie est double : la résolution est dégradée au centre
du champ de vue reconstruit et la fauchée ainsi que la gamme des angles
d'incidence disponible sont réduites. Plus
. L'effet est particulièrement probant le long
des côtes britanniques, la zone de transition entre les terres et la mer
s'élargissant nettement lorsque l'on s'éloigne du point sub-satellite
avec une apodisation classique, alors qu'elle est constante avec le multi-fenêtrage.
La contrepartie est double : la résolution est dégradée au centre
du champ de vue reconstruit et la fauchée ainsi que la gamme des angles
d'incidence disponible sont réduites. Plus 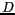 est petit, plus le champ reconstruit se réduit, comme l'illustre
le tableau 6.1 résumant les caractéristique
du champ reconstruit pour les différentes résolutions testées.
est petit, plus le champ reconstruit se réduit, comme l'illustre
le tableau 6.1 résumant les caractéristique
du champ reconstruit pour les différentes résolutions testées.
Table 1: Fauchée et gamme des angles d'incidences.
|
résolution isotrope au sol
|
fauchée
|
gamme d'angle d'incidences
|
|
55 km
|
1300 km
|
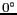 /
/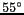
|
|
44 km
|
1100 km
|
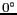 /
/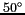
|
|
33 km
|
850 km
|
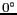 /
/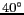
|
Les valeurs optimisées des paramètres
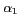 ,
, 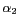 et
et 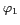 sont montrées sur la
figure
sont montrées sur la
figure ![[*]](file:///C|/texutils/l2h/icons/crossref.gif) . Les faibles valeurs atteintes par
. Les faibles valeurs atteintes par
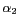 dans certaines zones conduisent à des amplitudes
des oscillations de GIBBS importantes. La hauteur des lobes
secondaires est alors proche de celle d'une fenêtre
rectangle. Les valeurs des deux facteurs de mérite (HSLL et
BEHM) de la figure
dans certaines zones conduisent à des amplitudes
des oscillations de GIBBS importantes. La hauteur des lobes
secondaires est alors proche de celle d'une fenêtre
rectangle. Les valeurs des deux facteurs de mérite (HSLL et
BEHM) de la figure ![[*]](file:///C|/texutils/l2h/icons/crossref.gif) sont à comparer avec celles de
la fenêtre de BLACKMAN : HSLL = -13.6 dB et BEHM =
98.7%.
sont à comparer avec celles de
la fenêtre de BLACKMAN : HSLL = -13.6 dB et BEHM =
98.7%.
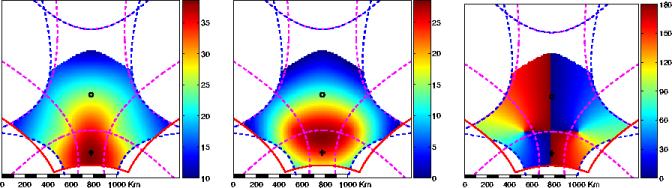
Figure 6.13: (De gauche à droite), paramètres
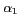 ,
, 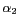 et
et 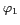 optimisés pour une résolution isotrope D=55km dans
le repère terrestre.
optimisés pour une résolution isotrope D=55km dans
le repère terrestre.
|
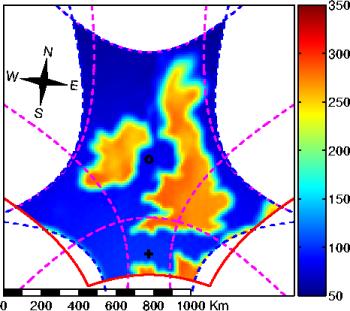
Figure 6.14: Projection de la carte de température reconstruite
et apodisée par la fenêtre de KAISER(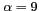 ) dans le repère terrestre. L'utilisation d'une seule
fenêtre pour l'ensemble des pixels conduit à une dégradation
de la résolution spatiale au fur et à mesure que l'on se rapproche
du bord du champ de vue : de 25 km sur la côte sud de l'Angleterre,
elle passe à 100 km au nord de l'Ecosse.
) dans le repère terrestre. L'utilisation d'une seule
fenêtre pour l'ensemble des pixels conduit à une dégradation
de la résolution spatiale au fur et à mesure que l'on se rapproche
du bord du champ de vue : de 25 km sur la côte sud de l'Angleterre,
elle passe à 100 km au nord de l'Ecosse.
|
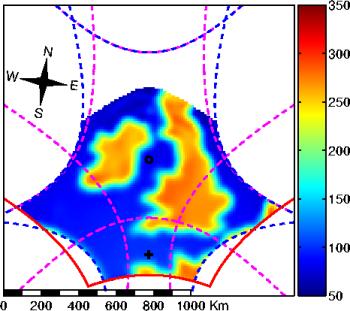
Figure 6.15: Application du multi-fenêtrage sur la scène
reconstruite : chaque pixel est apodisé par une fenêtre de KAISER
dont les paramètres ont été ajustés de façon à
obtenir une résolution spatiale isotrope de 55 km. Notons que cette
technique à pour conséquence de réduire le champ de vue exploitable.
|
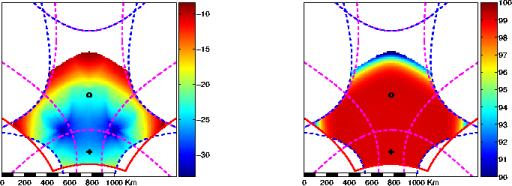
Figure 6.16: A Gauche, hauteur des lobes secondaires
en dB et, à droite, efficacité du lobe principal en % dans
le repère terrestre pour une résolution isotrope D=55km.
|
Les effets de ces lobes secondaires sur la qualité de l'estimation des
paramètres géophysiques ont été étudiés à travers l'étude du
comportement de la variable centrée
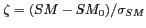 ,
, 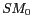 étant la valeur réelle de
l'humidité du sol, SM la valeur estimée et
étant la valeur réelle de
l'humidité du sol, SM la valeur estimée et
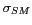 l'incertitude sur cette estimation.
l'incertitude sur cette estimation. 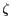 doit suivre une
loi gaussienne, avec une valeur moyenne
doit suivre une
loi gaussienne, avec une valeur moyenne
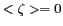 et une
déviation standard
et une
déviation standard
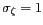 . Une valeur non nulle
pour
. Une valeur non nulle
pour 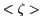 traduit un biais sur l'estimation de
l'humidité tandis qu'une déviation standard plus grande que 1
conduit à des valeurs estimées peu fiables, ce qui
traduit sans doute une sous-estimation.
traduit un biais sur l'estimation de
l'humidité tandis qu'une déviation standard plus grande que 1
conduit à des valeurs estimées peu fiables, ce qui
traduit sans doute une sous-estimation.
Les statistiques reportées dans le tableau 6.2 sont
celles de la variable centrée 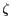 pour l'Europe de l'Ouest calculée lorsque sont appliqués
une fenêtre de BLACKMAN ou le multi-fenêtrage, en choisissant
la fonction de pondération exacte, dépendant de l'angle d'incidence,
ou au contraire une fonction de pondération moyenne. Chaque pixel contenant
une fraction pondérée de couvert végétal supérieure
à 20% est retenu.
pour l'Europe de l'Ouest calculée lorsque sont appliqués
une fenêtre de BLACKMAN ou le multi-fenêtrage, en choisissant
la fonction de pondération exacte, dépendant de l'angle d'incidence,
ou au contraire une fonction de pondération moyenne. Chaque pixel contenant
une fraction pondérée de couvert végétal supérieure
à 20% est retenu.
Alors qu'il est normalement possible de choisir la fonction
de pondération exacte pour chaque pixel lors de l'estimation
de l'humidité, il est plus simple
de supposer cette fonction identique dans tout le champ
reconstruit. Cependant, dans ce cas, les lobes secondaires
viennent dégrader les résultats lorsque le multi-fenêtrage
est utilisé. Les performances restent toutefois meilleures
pour le multi-fenêtrage que pour une apodisation classique
lorsque une fonction de pondération moyenne est appliquée.
Table 6.2: Statistiques sur la variable centrée 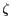 .
.
|
Fenêtre appliquée
|
Fonction de pondération
|
|
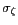
|
|
|
|
|
|
|
BLACKMAN
|
moyenne
|
+0.66
|
1.84
|
|
|
|
|
|
|
BLACKMAN
|
réelle
|
-0.04
|
0.99
|
|
|
|
|
|
|
Multi-fenêtrage
|
moyenne
|
+0.17
|
1.45
|
|
|
|
|
|
|
Multi-fenêtrage
|
réelle
|
-0.09
|
1.05
|
Biographie(s)
BESSEL, Friedrich Wilhelm
(22 Juillet 1784,
Minden, Westphalie - 17 Mars 1846, Konigsberg, Prusse)
Bessel ne s'est tourné vers les sciences que relativement
tard. Agé de 14 ans, il quitte l'école pour devenir apprenti
dans une société commerciale d'import-export à Bremen.
Alors qu'il ne touche aucun salaire, les activités et les
partenariat de cette société le pousse à étudier en parallèle
la géographie, l'espagnol et l'anglais. Il s'oriente alors
vers les problèmes de navigation liés au positionnement des
navires en pleine mer. Finalement, cette démarche le pousse
vers les mathématiques et l'astronomie.
En 1804, il écrit un mémoire sur ses calculs de l'orbite de
la comète de Halley effectués à partir de mesures réalisées
par Harriot en 1607. Heinrich Olbers, à qui il envoie ce
papier, reconnaît là un talent particulier et le pousse à
continuer dans cette voie. En 1806, il abandonne une vie
financièrement stable pour devenir assistant à
l'observatoire de Lilienthal. Continuant ses recherches sur
la position des étoiles, il devient directeur du nouvel
observatoire de Konigsberf, encore en construction, en 1810. Sous la
recommandation de Gauss, il reçoit le titre de docteur de
l'université de Gottingen, ce qui lui permet de devenir
officiellement professeur en astronomie et d'enseigner.
Bessel a été l'un des premiers astronome à reconnaître
l'importance de l'estimation des erreurs de mesures dans la
détermination de la position des astres. Il réduit les
données de Bradley sur la position de quelques milliers
d'étoile, déduisant les erreurs instrumentales causées par
la réfraction, éliminant les effets du déplacement de la
Terre.
Il introduit la fonction de Bessel dès 1817 lors d'une étude
du problème à 3 corps de Kepler. En 1824, Il publie un traité sur la
perturbation des orbites des planètes dans lequel il
complète l'analyse de ces fonctions.
En 1830, il publie la position moyenne et apparente
de 38 étoiles sur la période 1750-1850. En 1841, il déduit de la
variation périodique des trajectoires de Sirius et Procyon
la présence de système doubles, 21 ans avant leur
observation.




Next: Partie III
Up: 6. Passage au repère
Previous: 6.2 Rééchantillonnage des champs
nous
2005-03-31
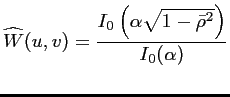
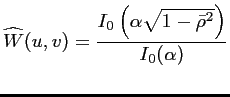
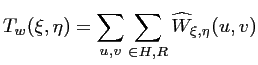 e
e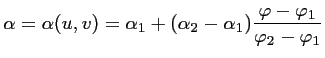
![]() imposée ne peut être atteinte dans l'ensemble du champ
de vue reconstruit. La figure 6.15 montre comment le
multi-fenêtrage a été appliqué à la scène présentée
sur la figure 6.14 pour une résolution
imposée ne peut être atteinte dans l'ensemble du champ
de vue reconstruit. La figure 6.15 montre comment le
multi-fenêtrage a été appliqué à la scène présentée
sur la figure 6.14 pour une résolution
![]() . L'effet est particulièrement probant le long
des côtes britanniques, la zone de transition entre les terres et la mer
s'élargissant nettement lorsque l'on s'éloigne du point sub-satellite
avec une apodisation classique, alors qu'elle est constante avec le multi-fenêtrage.
La contrepartie est double : la résolution est dégradée au centre
du champ de vue reconstruit et la fauchée ainsi que la gamme des angles
d'incidence disponible sont réduites. Plus
. L'effet est particulièrement probant le long
des côtes britanniques, la zone de transition entre les terres et la mer
s'élargissant nettement lorsque l'on s'éloigne du point sub-satellite
avec une apodisation classique, alors qu'elle est constante avec le multi-fenêtrage.
La contrepartie est double : la résolution est dégradée au centre
du champ de vue reconstruit et la fauchée ainsi que la gamme des angles
d'incidence disponible sont réduites. Plus ![]() est petit, plus le champ reconstruit se réduit, comme l'illustre
le tableau 6.1 résumant les caractéristique
du champ reconstruit pour les différentes résolutions testées.
est petit, plus le champ reconstruit se réduit, comme l'illustre
le tableau 6.1 résumant les caractéristique
du champ reconstruit pour les différentes résolutions testées.
![]() pour l'Europe de l'Ouest calculée lorsque sont appliqués
une fenêtre de BLACKMAN ou le multi-fenêtrage, en choisissant
la fonction de pondération exacte, dépendant de l'angle d'incidence,
ou au contraire une fonction de pondération moyenne. Chaque pixel contenant
une fraction pondérée de couvert végétal supérieure
à 20% est retenu.
pour l'Europe de l'Ouest calculée lorsque sont appliqués
une fenêtre de BLACKMAN ou le multi-fenêtrage, en choisissant
la fonction de pondération exacte, dépendant de l'angle d'incidence,
ou au contraire une fonction de pondération moyenne. Chaque pixel contenant
une fraction pondérée de couvert végétal supérieure
à 20% est retenu.
