Comme il est démontré dans le paragraphe précédent, la grille
d'échantillonnage des cartes de températures de brillances
n'est pas régulière dans le repère terrestre. Il est
toutefois possible, sous certaines conditions, d'obtenir la
valeur de la température de
brillance en tout point
![]() ne coïncidant pas avec
les noeuds de la grille d'échantillonnage
ne coïncidant pas avec
les noeuds de la grille d'échantillonnage
![]() et donc de ré-échantillonner la carte de température de
brillance dans le repère terrestre sur une grille
régulière, et ce, sans perte d'information ni
déformation.
et donc de ré-échantillonner la carte de température de
brillance dans le repère terrestre sur une grille
régulière, et ce, sans perte d'information ni
déformation.
Pour cela, seront considérées dans ce paragraphe des cartes de températures à bande passante limitée, soit que la méthode de reconstruction conduise directement à ce cas particulier, soit que ces cartes aient été apodisées.
Nous allons rappeler ici les expressions des fonctions de ré-échantillonnage, dites aussi d'interpolation, selon que les données sont initialement échantillonnées sur une grille cartésienne ou hexagonale.
Considérons l'image
![]() , échantillonnée sur une grille
cartésienne régulière à maille carrée avec
, échantillonnée sur une grille
cartésienne régulière à maille carrée avec
![]() ,
,
![]() et
et ![]() le pas d'échantillonnage.
La valeur de
le pas d'échantillonnage.
La valeur de ![]() au point
au point
![]() est liée à la transformée de FOURIER continue
est liée à la transformée de FOURIER continue
![]() de
de ![]() :
:
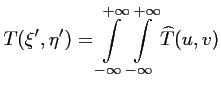 e e |
(6.22) |
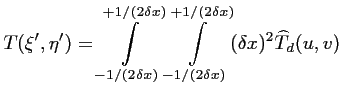 e e |
(6.23) |
 |
(6.24) | ||
 |
(6.25) | ||
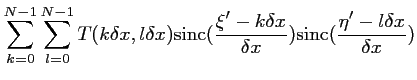 |
(6.26) |
| (6.27) |
La relation est considérablement
compliquée dans le cas d'un maillage hexagonal. Anterrieu et al.EricApod ont établi la
fonction d'interpolation dans ce cas :
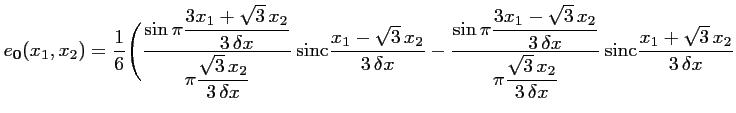 |
|||
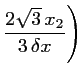 |
(6.28) |
Dans le cas de cartes de températures de brillance à bande
passante limitée, l'interpolation en point donnée
![]() peut être
effectuée à l'aide d'une simple transformée de
FOURIER discrète inverse du spectre
peut être
effectuée à l'aide d'une simple transformée de
FOURIER discrète inverse du spectre
![]() (obtenu
par exemple par une FFT de l'image initiale) :
(obtenu
par exemple par une FFT de l'image initiale) :
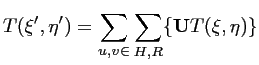 e e |
(6.29) |
De plus, d'après la propriété de translation de la transformée
de FOURIER, les composantes de FOURIER de
![]() sont égales à
sont égales à
![]() . La méthode
d'interpolation ou de rééchantillonnage employée devrait alors
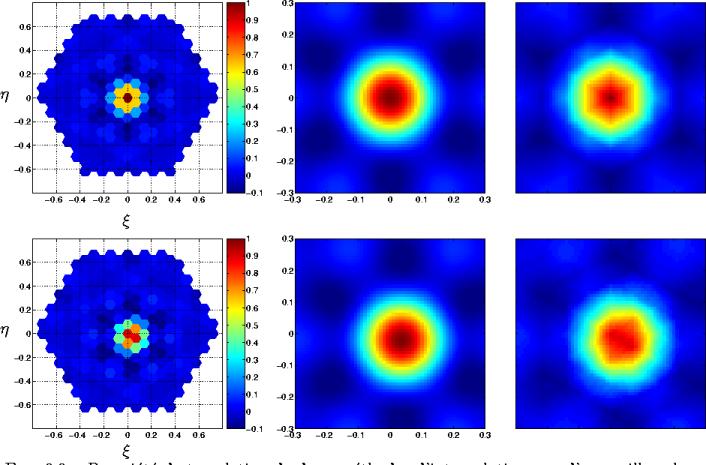
être indépendante de toute translation. Or, la figure 6.9
montre que, si l'interpolation de SHANNON est bien indépendante
de la translation, une interpolation bilinéaire, telle qu'utilisée
par Camps et al. CampsHexa1 ne l'est clairement pas, l'image
rééchantillonnée faisant apparaître des artefacts dus à
l'échantillonnage hexagonal de l'image initiale.
. La méthode
d'interpolation ou de rééchantillonnage employée devrait alors
être indépendante de toute translation. Or, la figure 6.9
montre que, si l'interpolation de SHANNON est bien indépendante
de la translation, une interpolation bilinéaire, telle qu'utilisée
par Camps et al. CampsHexa1 ne l'est clairement pas, l'image
rééchantillonnée faisant apparaître des artefacts dus à
l'échantillonnage hexagonal de l'image initiale.
|