Next: 6.2 Rééchantillonnage des champs
Up: 6. Passage au repère
Previous: 6. Passage au repère
Contenu
Si les lobes arrières des antennes sont négligés, le radiomètre
imageur à synthèse d'ouverture observe l'intégralité du
demi-espace situé devant lui. Dans le repère des cosinus directeurs
appelé aussi repère instrumental ou repère des antennes, cet
espace est contenu dans le cercle unité (voir Fig. 6.2).
L'étendue du champ de vue observé vaut alors
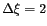 . A l'intérieur de ce cercle, la température
d'antenne dépend de la contribution de la terre et de la portion visible
de la voûte céleste, appelée simplement Ciel par la suite.
. A l'intérieur de ce cercle, la température
d'antenne dépend de la contribution de la terre et de la portion visible
de la voûte céleste, appelée simplement Ciel par la suite.
Or, la position et la forme de la terre à l'intérieur du cercle
unité dépendent notamment de l'inclinaison 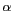 de l'instrument. Ce paramètre peut être ajusté
de façon à augmenter la largeur de fauchée dans le champ de vue
reconstruit PhilFOV. La figure 6.1 décrit les
référentiels qui entrent en jeu lors de la paramétrisation de
la position de la terre et du ciel dans le champ de vue observé. Rappelons
que le déplacement de l'instrument se fait selon l'axe
de l'instrument. Ce paramètre peut être ajusté
de façon à augmenter la largeur de fauchée dans le champ de vue
reconstruit PhilFOV. La figure 6.1 décrit les
référentiels qui entrent en jeu lors de la paramétrisation de
la position de la terre et du ciel dans le champ de vue observé. Rappelons
que le déplacement de l'instrument se fait selon l'axe 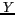 .
.
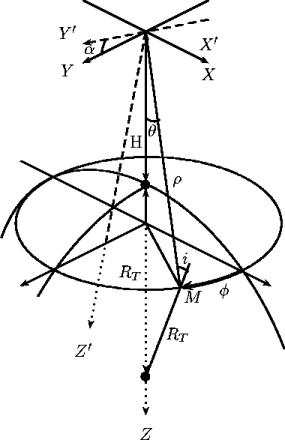
Figure 6.1:
Référentiels utilisés dans la caractérisation du
champ de vue observé d'un RISO. Le déplacement se fait le long
de l'axe Y. Il peut être choisi d'incliner le plan
contenant le réseau interférométrique d'un angle
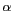 . Les cosinus directeurs
. Les cosinus directeurs 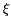 et
et 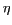 sont directement liés
aux coordonnées polaires (
sont directement liés
aux coordonnées polaires (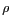 ,
,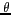 ,
,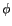 )
désignant respectivement la distance à la source, la
colatitude et l'azimut :
)
désignant respectivement la distance à la source, la
colatitude et l'azimut :
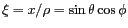 et
et
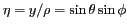 .
.
|
Cas
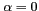
Le repère considéré est alors 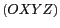 .
L'instrument étant situé à une altitude H, la position du
point
.
L'instrument étant situé à une altitude H, la position du
point 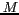 observé est définie par ses coordonnées
cartésiennes
observé est définie par ses coordonnées
cartésiennes 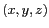 ou par ses coordonnées
polaires
ou par ses coordonnées
polaires
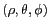 où
où 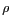 est la distance
mesurée depuis
est la distance
mesurée depuis 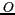 ,
, 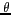 la colatitude et
la colatitude et 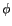 l'azimut. L'incidence en ce point est donnée par l'angle
l'azimut. L'incidence en ce point est donnée par l'angle
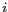 . Les cosinus directeurs sont alors :
. Les cosinus directeurs sont alors :
L'horizon terrestre qui détermine la limite entre la terre
et le ciel est caractérisé par une incidence
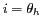 . La
colatitude pour les points de l'horizon est :
. La
colatitude pour les points de l'horizon est :
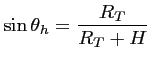 |
(6.3) |
où 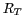 est le rayon de la terre supposée sphérique. Dans le repère des cosinus
directeurs
est le rayon de la terre supposée sphérique. Dans le repère des cosinus
directeurs
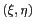 , la terre est alors un disque de rayon
, la terre est alors un disque de rayon
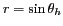 centré en
centré en 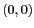 , dont le périmètre est caractérisé par l'équation de l'horizon terrestre :
, dont le périmètre est caractérisé par l'équation de l'horizon terrestre :
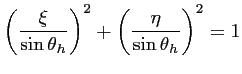 |
(6.4) |
Cas
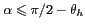
Pour 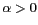 , le repère considéré est
, le repère considéré est 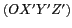 et les
cosinus directeurs sont
et les
cosinus directeurs sont 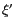 et
et 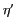 . Le passage du
référentiel
. Le passage du
référentiel 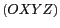 à ce référentiel se fait
simplement à l'aide de la matrice de rotation d'angle
à ce référentiel se fait
simplement à l'aide de la matrice de rotation d'angle 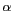 :
:
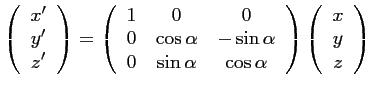 |
(6.5) |
ce qui, pour les cosinus directeurs, revient à :
Le passage de 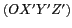 à
à 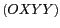 se fait
simplement à l'aide de la matrice de rotation d'angle
se fait
simplement à l'aide de la matrice de rotation d'angle 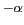 :
:
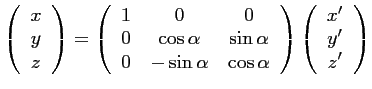 |
(6.8) |
Dans le repère des cosinus directeurs, le passage d'un repère à
l'autre se fait alors ainsi :
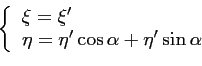 |
|
|
(6.9) |
Dans le repère
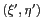 , la terre est alors délimitée par une ellipse de
grand axe
, la terre est alors délimitée par une ellipse de
grand axe
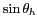 et de petit axe
et de petit axe
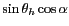 centrée en
centrée en
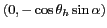 :
:
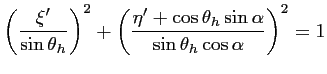 |
(6.10) |
Cas
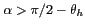
La relation (6.10) n'est valable que pour des inclinaisons
telles que
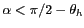 . Au delà de cette limite, une partie
de la terre est située dans le demi-espace arrière de l'instrument.
Dans le repère des cosinus directeurs, l'ellipse vient couper le cercle
unité aux points d'intersections :
. Au delà de cette limite, une partie
de la terre est située dans le demi-espace arrière de l'instrument.
Dans le repère des cosinus directeurs, l'ellipse vient couper le cercle
unité aux points d'intersections :
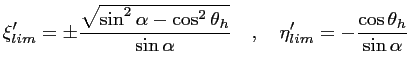 |
(6.11) |
La terre est délimitée par l'ellipse décrite par la relation (6.11)
au dessus de ces points et par le cercle unité en dessous.
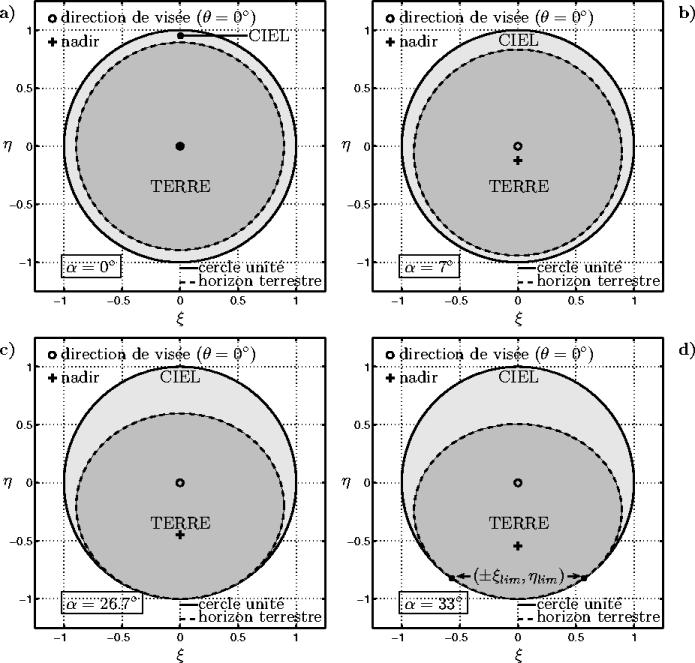
Figure 6.2: Modification de la forme de la terre dans le
repère des cosinus directeurs avec l'inclinaison de l'instrument (H=775
km et
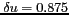 ). a) L'horizon terrestre est un cercle
pour une inclinaison nulle et b) une ellipse pour une inclinaison
faible. c) L'inclinaison
). a) L'horizon terrestre est un cercle
pour une inclinaison nulle et b) une ellipse pour une inclinaison
faible. c) L'inclinaison
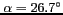 est l'inclinaison critique
est l'inclinaison critique
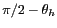 . d) L'inclinaison
. d) L'inclinaison
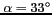 est proche de l'inclinaison prévue pour MIRAS.
Dans ce cas, l'horizon terrestre décrit une ellipse dans sa partie supérieure
et le cercle unité dans sa partie inférieure.
est proche de l'inclinaison prévue pour MIRAS.
Dans ce cas, l'horizon terrestre décrit une ellipse dans sa partie supérieure
et le cercle unité dans sa partie inférieure.
|
La figure 6.2 illustre la position de la terre dans le
cercle unité pour quatre inclinaisons de l'instrument :
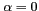 ,
,
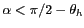 ,
,
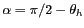 ,
,
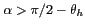 , avec H = 755 km. Dans le dernier
cas, l'inclinaison
, avec H = 755 km. Dans le dernier
cas, l'inclinaison
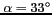 est proche de l'inclinaison qu'aura l'instrument
MIRAS.
est proche de l'inclinaison qu'aura l'instrument
MIRAS.
Les relations entre le champ de vue et l'intervalle
d'échantillonnage du domaine de FOURIER exprimées
plus haut permettent de trouver la valeur de 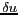 remplissant le critère de SHANNON-NYQUIST. La largeur du
champ de vue observé étant
remplissant le critère de SHANNON-NYQUIST. La largeur du
champ de vue observé étant
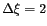 (diamètre du
cercle unité), l'intervalle d'échantillonnage doit être tel
que :
(diamètre du
cercle unité), l'intervalle d'échantillonnage doit être tel
que :
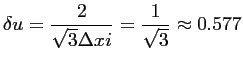 |
(6.12) |
pour un maillage hexagonal, et :
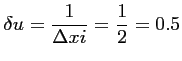 |
(6.13) |
pour un maillage cartésien. Or, que ce soit dans le cas de
MIRAS ou du HUT2D, il a été choisi une distance entre les
antennes conduisant à un sous-échantillonnage du domaine de
FOURIER (
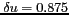 pour MIRAS et
pour MIRAS et
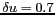 pour HUT2D) et donc à un repliement du cercle unité à
l'intérieur du champ de vue
reconstruit. Ce choix se justifie en remarquant qu'en
augmentant la distance entre les antennes, la plus grande
distance entre deux antennes du réseau interférométrique
augmente elle aussi, améliorant ainsi la résolution spatiale
pour HUT2D) et donc à un repliement du cercle unité à
l'intérieur du champ de vue
reconstruit. Ce choix se justifie en remarquant qu'en
augmentant la distance entre les antennes, la plus grande
distance entre deux antennes du réseau interférométrique
augmente elle aussi, améliorant ainsi la résolution spatiale
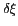 . On remarquera que les repliements
(aussi nommés alias) peuvent tout
aussi bien être vus comme les chevauchements de répliques
situées dans les mailles contiguës.
. On remarquera que les repliements
(aussi nommés alias) peuvent tout
aussi bien être vus comme les chevauchements de répliques
situées dans les mailles contiguës.
Pour le HUT2D, on distingue à l'intérieur du champ de vue reconstruit (FOV pour
Field Of View, ici un carré de
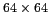 pixels) le champ de vue exempt
de repliement (AFFOV pour Alias Free Field Of
View). Etant donnée l'altitude standard de vol pour le
HUT2D, ces zones aliasées correspondent uniquement au
repliement de la terre dans le FOV (voir Fig.
pixels) le champ de vue exempt
de repliement (AFFOV pour Alias Free Field Of
View). Etant donnée l'altitude standard de vol pour le
HUT2D, ces zones aliasées correspondent uniquement au
repliement de la terre dans le FOV (voir Fig. ![[*]](file:///C|/texutils/l2h/icons/crossref.gif) ).
).
Pour MIRAS, le
champ de vue observé est composée de la Terre et du
Ciel. Dans un deuxième temps, on distingue donc différentes
zones à l'intérieur du champ de vue reconstruit (un hexagone
de
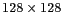 pixels) :
pixels) :
- la zone exempte d'aliasing. Elle est elle-même composée
de deux zones :
- une zone ne comportant aucun repliement (un hexagone déformé au centre
du champ de vue, en rouge sur la figure 6.4-c)
- une zone dans laquelle vient s'étendre une réplique du Ciel (en orange
Fig. 6.4-c). Il est possible de retrouver la valeur de
la température de brillance 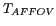 dans une zone élargie en retranchant aux visibilités
mesurées par l'instrument les visibilités correspondant à la contribution
du Ciel, à condition de connaître la distribution des températures
de brillances
dans une zone élargie en retranchant aux visibilités
mesurées par l'instrument les visibilités correspondant à la contribution
du Ciel, à condition de connaître la distribution des températures
de brillances 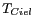 dans cette zone. Il suffit de remarquer que la relation entre
les visibilités et la température de brillance (3.38)
est linéaire.
dans cette zone. Il suffit de remarquer que la relation entre
les visibilités et la température de brillance (3.38)
est linéaire.
La carte de température de brillance dans cette zone
élargie exempte d'aliasing sera donc reconstruite à
partir des visibilités 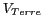 , corrigées de la
contribution du Ciel. Par la suite, les cartes de
, corrigées de la
contribution du Ciel. Par la suite, les cartes de  seront
reconstruites dans toute cette zone (appelée abusivement
zone exempte d'aliasing ou AFFOV) et les visibilités
seront
reconstruites dans toute cette zone (appelée abusivement
zone exempte d'aliasing ou AFFOV) et les visibilités 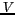 désigneront les visibilités corrigées.
désigneront les visibilités corrigées.
- la zone aliasée. Cette zone ne pourra pas être
exploitée lors de la reconstruction. On distingue quatre
catégories dans cette zone :
- le ciel. Cette zone étant située au-delà de
l'horizon terrestre, elle n'est pas exploitée (en bleu nuit dans
Fig. ![[*]](file:///C|/texutils/l2h/icons/crossref.gif) -c).
-c).
- les repliements dus à :
- une réplique la Terre (cyan, Fig. 6.4)
- une réplique de la Terre et à une réplique du Ciel (azur, Fig.
6.4)
- deux répliques de Terre (bleu foncé, Fig. 6.4)
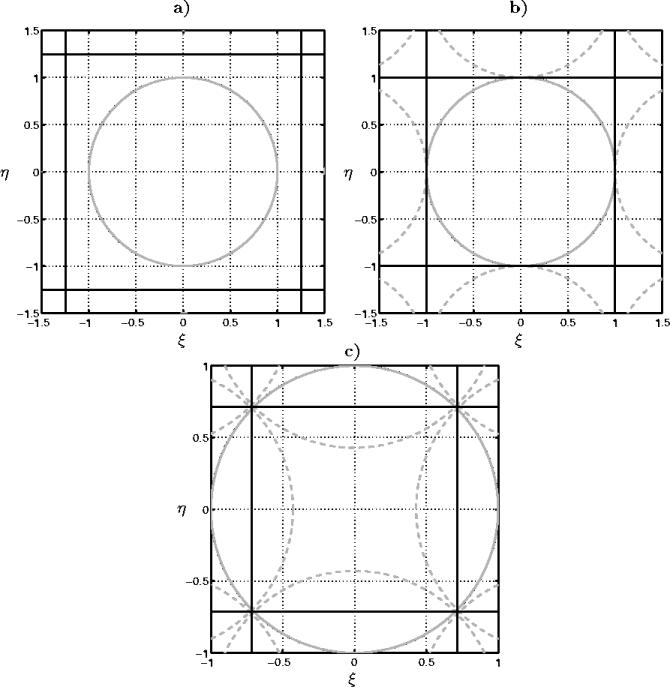
Figure 6.3: Composition du champ de vue reconstruit du HUT2D
pour plusieurs distances entre deux antennes du réseau interférométrique.
A l'intérieur de la maille carrée (
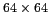 pixels), on retrouve le cercle unité (traits pleins)
qui représente le demi-espace qu'observe l'instrument. a) L'espace
pixels), on retrouve le cercle unité (traits pleins)
qui représente le demi-espace qu'observe l'instrument. a) L'espace
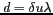 entre les antennes conduit à un sur-échantillonnage
du domaine de FOURIER (
entre les antennes conduit à un sur-échantillonnage
du domaine de FOURIER (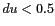 ) et le cercle unité est largement compris dans le champ
de vue reconstruit. b) L'espace entre les antennes est choisi
de façon à parfaitement répondre au critère de SHANNON-NYQUIST,
) et le cercle unité est largement compris dans le champ
de vue reconstruit. b) L'espace entre les antennes est choisi
de façon à parfaitement répondre au critère de SHANNON-NYQUIST,
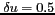 et le cercle unité est tangent au bord de la maille.
c) La valeur retenue
et le cercle unité est tangent au bord de la maille.
c) La valeur retenue
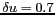 pour l'instrument réel, conduit à un sous-échantillonnage
du domaine de FOURIER et au repliement du cercle unité
à l'intérieur du champ de vue reconstruit (traits pointillés).
La zone exempte de repliement (AFFOV), contenue à l'intérieur des
pointillés, est la seule zone exploitable après la reconstruction.
pour l'instrument réel, conduit à un sous-échantillonnage
du domaine de FOURIER et au repliement du cercle unité
à l'intérieur du champ de vue reconstruit (traits pointillés).
La zone exempte de repliement (AFFOV), contenue à l'intérieur des
pointillés, est la seule zone exploitable après la reconstruction.
|
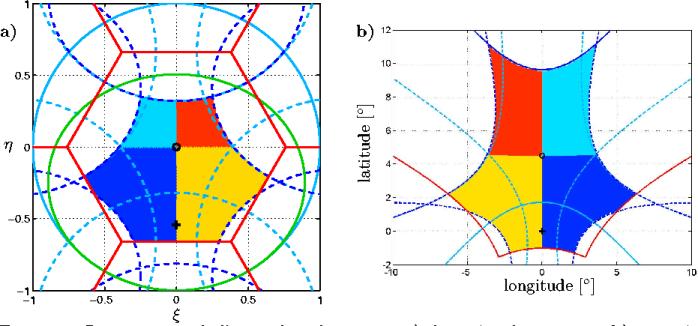
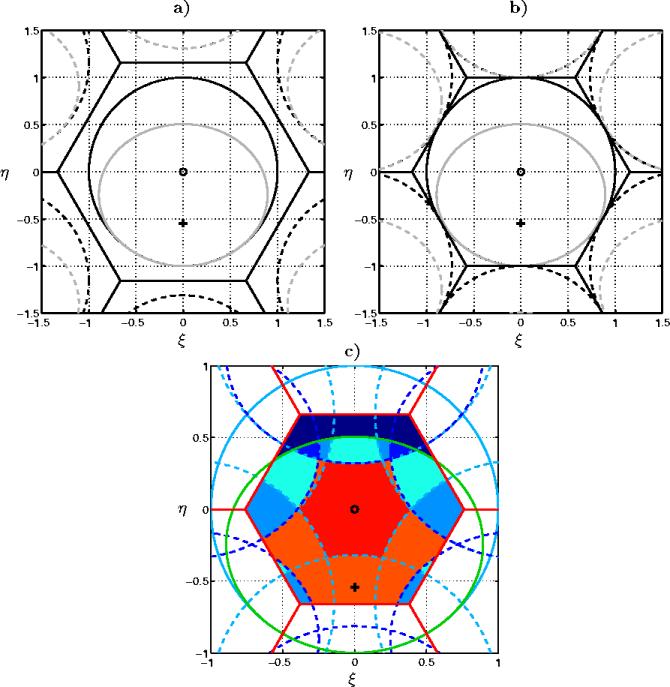
Figure 6.4: Composition du champ de vue reconstruit de MIRAS
pour plusieurs distances entre deux antennes du réseau interférométrique.
A l'intérieur de la maille hexagonale (
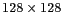 pixels), on retrouve le cercle unité (traits pleins
en noir) dans lequel on distingue l'ellipse représentant la Terre (traits
plein en gris), et le Ciel (entre l'ellipse et le cercle unité). a) L'espace
pixels), on retrouve le cercle unité (traits pleins
en noir) dans lequel on distingue l'ellipse représentant la Terre (traits
plein en gris), et le Ciel (entre l'ellipse et le cercle unité). a) L'espace
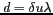 entre les antennes conduit à un sur-échantillonnage
du domaine de FOURIER (
entre les antennes conduit à un sur-échantillonnage
du domaine de FOURIER (
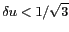 ) et le cercle unité est largement compris
dans le champ de vue reconstruit. b) L'espace entre les antennes
est choisi de façon à parfaitement répondre au critère
de SHANNON-NYQUIST,
) et le cercle unité est largement compris
dans le champ de vue reconstruit. b) L'espace entre les antennes
est choisi de façon à parfaitement répondre au critère
de SHANNON-NYQUIST,
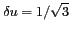 et le cercle unité est tangent au bord de
la maille. c) La valeur retenue
et le cercle unité est tangent au bord de
la maille. c) La valeur retenue
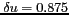 pour l'instrument réel, conduit à un sous-échantillonnage
du domaine de FOURIER et au repliement du cercle unité
à l'intérieur du champ de vue reconstruit (traits pointillés).
Une zone élargie, abusivement dite exempte de repliement, représentée
par les zones remplies des deux gris les plus clairs, est la seule zone exploitable
après la reconstruction.
pour l'instrument réel, conduit à un sous-échantillonnage
du domaine de FOURIER et au repliement du cercle unité
à l'intérieur du champ de vue reconstruit (traits pointillés).
Une zone élargie, abusivement dite exempte de repliement, représentée
par les zones remplies des deux gris les plus clairs, est la seule zone exploitable
après la reconstruction.
|
Le passage du repère des antennes dont les coordonnées sont
les cosinus directeurs au repère terrestre dont les
coordonnées sont les couples (latitude,longitude) est décrit
ci-dessous.
La première étape consiste à passer, le cas échéant,
des coordonnées
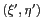 correspondant à un instrument incliné, aux coordonnées
correspondant à un instrument incliné, aux coordonnées
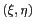 ainsi que décrit dans la section précédente
par la relation 6.9.
ainsi que décrit dans la section précédente
par la relation 6.9.
Dans un deuxième temps, il s'agit de passer du repère des
antennes au repère terrestre (OXYZ), en
considérant l'altitude 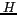 de l'instrument et
de l'instrument et 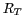 le rayon
terrestre :
le rayon
terrestre :
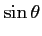 |
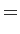 |
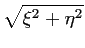 |
(6.14) |
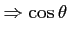 |
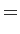 |
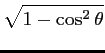 |
(6.15) |
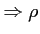 |
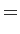 |
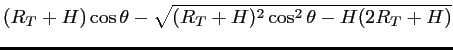 |
(6.16) |
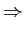 |
|
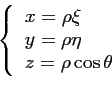 |
(6.17) |
Dans un troisième temps, si 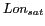 et
et 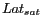 sont respectivement la
longitude et latitude du point sub-satellite (en radian), le passage au
repère terrestre se fait alors à l'aide de deux matrices de
rotation
sont respectivement la
longitude et latitude du point sub-satellite (en radian), le passage au
repère terrestre se fait alors à l'aide de deux matrices de
rotation 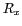 et
et 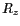 , respectivement d'un angle
, respectivement d'un angle
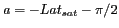 autour de l'axe
autour de l'axe 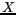 et d'un angle
et d'un angle
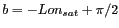 autour de l'axe
autour de l'axe 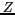 :
:
Les coordonnées cartésiennes
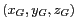 dans le repère de
Greenwich sont alors :
dans le repère de
Greenwich sont alors :
![$\displaystyle [x_G~y_G~z_G] = R_Z R_X \left[ \begin{array}{c} x\\ y\\ z-(R_T+H) \end{array} \right]$](img939.gif) |
(6.20) |
Finalement, la longitude 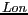 et la latitude
et la latitude 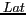 du point courant
sont :
du point courant
sont :
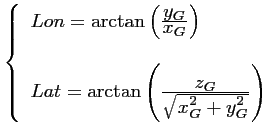 |
(6.21) |
Les figures 6.5, 6.6 et 6.7
illustrent les caractéristiques du passage du repère des antennes au
repère terrestre pour l'instrument MIRAS (H=755 km,
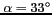 ).
).
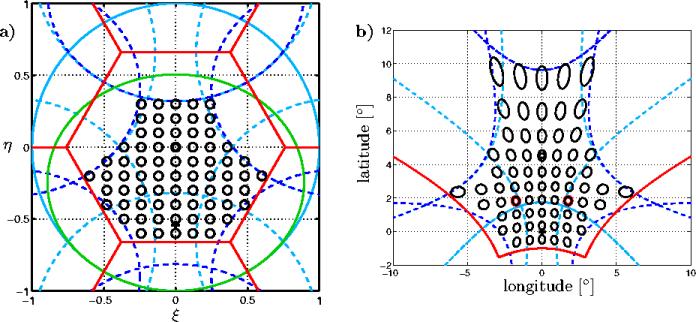
La figure 6.5 montrent comment la résolution
spatiale varie dans le champ de vue reconstruit projeté dans le repère
terrestre. Alors que la résolution spatiale est isotrope dans tout le plan
des cosinus directeurs (symbolisé par des cercles de rayons
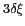 dans la figure 6.5-a), elle varie
selon les directions et la position du pixel considéré dans le champ
de vue reconstruit dans le repère terrestre. La résolution spatiale
en ce pixel est déterminée par le grand axe d'une ellipse (résolution
radiale) et, dans une direction orthogonale, par son petit axe (résolution
transverse).
dans la figure 6.5-a), elle varie
selon les directions et la position du pixel considéré dans le champ
de vue reconstruit dans le repère terrestre. La résolution spatiale
en ce pixel est déterminée par le grand axe d'une ellipse (résolution
radiale) et, dans une direction orthogonale, par son petit axe (résolution
transverse).
Cette déformation se comprend
simplement en faisant l'hypothèse d'une terre plate et
en se rappelant que la résolution spatiale d'un RISO est
celle d'une antenne dont le diamètre est égale à la plus
grand distance entre deux antennes. Dans le cas d'un
instrument non incliné, l'intersection du gain
de cette antenne synthétisée avec une surface
plane est un cercle centré sur le point sub-satellite (la
résolution spatiale est isotrope) et va
naturellement s'allonger en une ellipse au fur et à mesure
que l'on s'éloigne du centre du champ de vue.
A ce phénomène s'additionne l'effet de la rotondité de la Terre
qui va conduire à une modification de l'orientation de l'ellipse au fur
et à mesure que l'on s'éloigne de l'axe 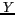 , le long du déplacement du satellite, ainsi que l'on peut le
remarquer sur la figure 6.5-d. Ainsi, la résolution
n'est isotrope que pour deux pixels situés de part et d'autre de l'axe
, le long du déplacement du satellite, ainsi que l'on peut le
remarquer sur la figure 6.5-d. Ainsi, la résolution
n'est isotrope que pour deux pixels situés de part et d'autre de l'axe
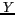 , proches du centre des deux cercles marqués de rouge sur cette
même figure.
, proches du centre des deux cercles marqués de rouge sur cette
même figure.
D'autre part, comme le montre la figure (6.5), une grille
régulière dans le repère terrestre ne l'est pas dans le repère
des cosinus directeurs. Le paragraphe suivant est consacré aux rééchantillonnages
nécessaires à l'obtention d'une grille régulière dans le
repère terrestre.
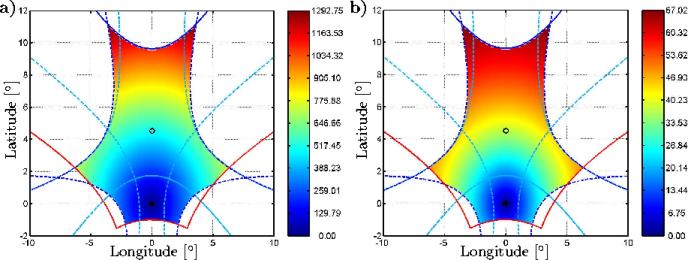
Les figures 6.8-a et 6.8-b permettent
d'établir respectivement, d'une part la variation de la distance mesurée
par rapport au point sub-satellite et les dimensions du champ de vue reconstruit
et d'autre part la variation de l'angle d'incidence sous lequel est effectuée
la mesure, rappelant dans le même temps la capacité multi-angulaire
des radiomètres imageurs à synthèse d'ouverture.
Figure 6.5: Déformation de la fonction de transfert
instrumentale lors du passage du repère des antennes au repère terrestre
: a), la résolution spatiale est isotrope pour tout les pixels
du plan des cosinus directeurs alors que b), dans le repère terrestre,
elle varie selon les directions et la position du pixel dans le champ de vue
reconstruit. On observe aussi la déformation de la grille régulière
dans le domaine des antennes à travers la courbure des lignes joignant
le centre des ellipses.
|
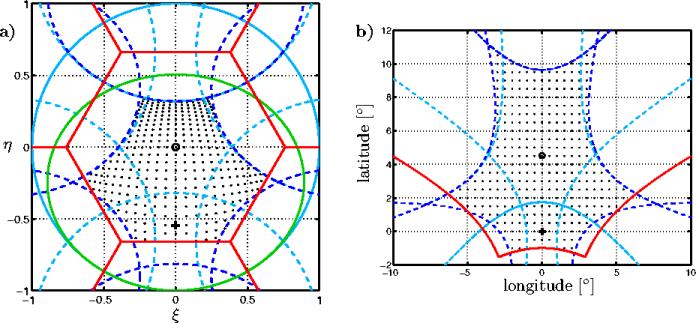
Figure 6.6: Déformation d'une grille régulière
dans le repère terrestre lors du passage dans le repère des antennes.
Le traitement des paramètres géophysiques demande à travailler
sur une grille régulière dans le repère terrestre. Il est donc
nécessaire d'interpoler la carte de température de brillance dans
le domaine des cosinus directeurs, puisque ces points ne correspondent pas
aux noeuds de la grille d'échantillonnage.
|
Figure 6.7: Renversement de l'image lors du passage a)
du repère des antennes b) au repère terrestre : le changement
de repère conduit à un renversement de l'image par rapport à
l'axe 
|
Figure 6.8: a) Distances ([km]) mesurées
par rapport au point sub-satellite et b) variation de l'angle
d'incidence ([ ]) de la mesure (champ de vue reconstruit, repère terrestre).
]) de la mesure (champ de vue reconstruit, repère terrestre).
|




Next: 6.2 Rééchantillonnage des champs
Up: 6. Passage au repère
Previous: 6. Passage au repère
nous
2005-03-31
![]() . A l'intérieur de ce cercle, la température
d'antenne dépend de la contribution de la terre et de la portion visible
de la voûte céleste, appelée simplement Ciel par la suite.
. A l'intérieur de ce cercle, la température
d'antenne dépend de la contribution de la terre et de la portion visible
de la voûte céleste, appelée simplement Ciel par la suite.
![]() de l'instrument. Ce paramètre peut être ajusté
de façon à augmenter la largeur de fauchée dans le champ de vue
reconstruit PhilFOV. La figure 6.1 décrit les
référentiels qui entrent en jeu lors de la paramétrisation de
la position de la terre et du ciel dans le champ de vue observé. Rappelons
que le déplacement de l'instrument se fait selon l'axe
de l'instrument. Ce paramètre peut être ajusté
de façon à augmenter la largeur de fauchée dans le champ de vue
reconstruit PhilFOV. La figure 6.1 décrit les
référentiels qui entrent en jeu lors de la paramétrisation de
la position de la terre et du ciel dans le champ de vue observé. Rappelons
que le déplacement de l'instrument se fait selon l'axe ![]() .
.
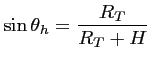
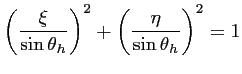
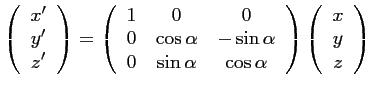
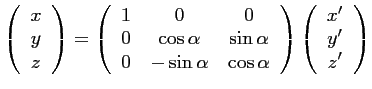
![]()
![]() . Au delà de cette limite, une partie
de la terre est située dans le demi-espace arrière de l'instrument.
Dans le repère des cosinus directeurs, l'ellipse vient couper le cercle
unité aux points d'intersections :
. Au delà de cette limite, une partie
de la terre est située dans le demi-espace arrière de l'instrument.
Dans le repère des cosinus directeurs, l'ellipse vient couper le cercle
unité aux points d'intersections :
![]() remplissant le critère de SHANNON-NYQUIST. La largeur du
champ de vue observé étant
remplissant le critère de SHANNON-NYQUIST. La largeur du
champ de vue observé étant
![]() (diamètre du
cercle unité), l'intervalle d'échantillonnage doit être tel
que :
(diamètre du
cercle unité), l'intervalle d'échantillonnage doit être tel
que :
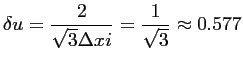
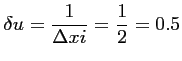
![]() , corrigées de la
contribution du Ciel. Par la suite, les cartes de
, corrigées de la
contribution du Ciel. Par la suite, les cartes de ![]() seront
reconstruites dans toute cette zone (appelée abusivement
zone exempte d'aliasing ou AFFOV) et les visibilités
seront
reconstruites dans toute cette zone (appelée abusivement
zone exempte d'aliasing ou AFFOV) et les visibilités ![]() désigneront les visibilités corrigées.
désigneront les visibilités corrigées.
![]() -c).
-c).
![]() correspondant à un instrument incliné, aux coordonnées
correspondant à un instrument incliné, aux coordonnées
![]() ainsi que décrit dans la section précédente
par la relation 6.9.
ainsi que décrit dans la section précédente
par la relation 6.9.
![]() de l'instrument et
de l'instrument et ![]() le rayon
terrestre :
le rayon
terrestre :

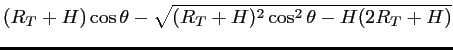
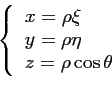
![]() et
et ![]() sont respectivement la
longitude et latitude du point sub-satellite (en radian), le passage au
repère terrestre se fait alors à l'aide de deux matrices de
rotation
sont respectivement la
longitude et latitude du point sub-satellite (en radian), le passage au
repère terrestre se fait alors à l'aide de deux matrices de
rotation ![]() et
et ![]() , respectivement d'un angle
, respectivement d'un angle
![]() autour de l'axe
autour de l'axe ![]() et d'un angle
et d'un angle
![]() autour de l'axe
autour de l'axe ![]() :
:
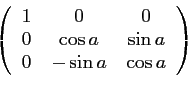
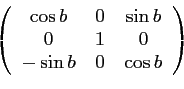
![$\displaystyle [x_G~y_G~z_G] = R_Z R_X \left[ \begin{array}{c} x\\ y\\ z-(R_T+H) \end{array} \right]$](img939.gif)
![]() et la latitude
et la latitude ![]() du point courant
sont :
du point courant
sont :
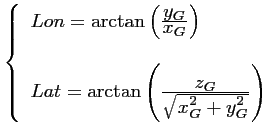
![]() dans la figure 6.5-a), elle varie
selon les directions et la position du pixel considéré dans le champ
de vue reconstruit dans le repère terrestre. La résolution spatiale
en ce pixel est déterminée par le grand axe d'une ellipse (résolution
radiale) et, dans une direction orthogonale, par son petit axe (résolution
transverse).
dans la figure 6.5-a), elle varie
selon les directions et la position du pixel considéré dans le champ
de vue reconstruit dans le repère terrestre. La résolution spatiale
en ce pixel est déterminée par le grand axe d'une ellipse (résolution
radiale) et, dans une direction orthogonale, par son petit axe (résolution
transverse).
![]() , le long du déplacement du satellite, ainsi que l'on peut le
remarquer sur la figure 6.5-d. Ainsi, la résolution
n'est isotrope que pour deux pixels situés de part et d'autre de l'axe
, le long du déplacement du satellite, ainsi que l'on peut le
remarquer sur la figure 6.5-d. Ainsi, la résolution
n'est isotrope que pour deux pixels situés de part et d'autre de l'axe
![]() , proches du centre des deux cercles marqués de rouge sur cette
même figure.
, proches du centre des deux cercles marqués de rouge sur cette
même figure.