Contenu

• 7.2.1 La transformée de FOURIER inverse
• 7.2.2 La méthode CLEAN
• 7.2.3 L'algorithme de calibration par points chauds

7.2 Méthodes de reconstruction non régularisées

Avant d'aborder les méthodes développées par deux autres équipes impliquées dans le projet SMOS, il est nécessaire de bien comprendre pourquoi la transformée de FOURIER ne saurait être un opérateur de reconstruction valable.

7.2.1 La transformée de FOURIER inverse

Même s'il est commode de rapprocher le fonctionnement des radiomètres imageurs à synthèse d'ouverture de celui de la transformée de FOURIER, l'opérateur $\mathbf{G}$ n'en reste pas moins différent de l'opérateur $U$ . Afin de mettre en évidence cette assertion, les composantes de FOURIER et les visibilités sont calculées pour différents niveaux de résolution d'une même scène. La figure 7.1 montre la scène $T_o$ à son plus haut niveau de résolution (Fig. 7.1-a), ses composantes de FOURIER (Fig. 7.1-b) et les visibilités telles que mesurées par un RISO (Fig. -c).

Notons qu'une échelle logarithmique a été utilisée afin d'améliorer la lisibilité des figures, la figure 7.1-b montrant  $\log_{10}\frac{\vert\vert \mathbf{U}T_o \vert\vert _F}{\left\{\mathbf{U}T_o \right\}(0,0)}$ et la figure 7.1-c montrant  $\log_{10}\frac{\vert\vert \mathbf{G}T_o \vert\vert _F}{V(0,0)}$ .

Si maintenant la scène observée est une version à basse résolution de $T_o$ (Fig. 7.2-a) ne comportant de composantes de FOURIER non nulles qu'à l'intérieur de la bande passante (Fig. 7.2-b), peu de différences existent entre ces composantes de FOURIER et les visibilités mesurées (Fig. 7.2-c).

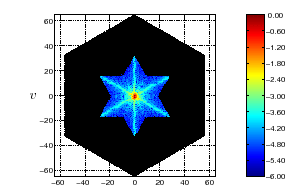
Cependant, lorsque la scène observée est une distribution uniforme de température égale à la température moyenne de la scène $T_o$ , l'instrument fournit des visibilités non nulles pour l'ensemble des fréquences de la bande passante (Fig. 7.3), alors une scène uniforme n'a de composante de Fourier qu'à la fréquence nulle.

Et même lorsque la scène observée est une version hautes fréquences de $T_o$ (Fig. 7.4-a) ne comportant de composantes de FOURIER non nulles qu'en dehors de l'étoile (Fig. 7.4-b), l'instrument fournit tout de même des visibilités non nulles à l'intérieur de la bande passante (Fig. 7.4-c), à des fréquences auxquelles on ne retrouve aucune composante de FOURIER.

En effet, pour un instrument idéal (gains d'antennes tous identiques, pas de phénomène de décorrélation spatiale), l'action de la matrice de modélisation sur $T_o$ n'est pas celle de $\mathbf{U}$ sur $T_o$ mais plutôt celle de $\mathbf{Z}^*\mathbf{U}$ sur $\widetilde {T} = \vert F(\mathbf{\xi})\vert^2T_o(\mathbf{\xi})/\sqrt{1-\vert\vert\mathbf{\xi}\vert\vert^2}$ appelée température modifiée. Or, cette température modifiée, à cause de la multiplication par le module du gain d'antenne et de la division par le facteur d'obliquité, n'est pas une distribution uniforme, même si la scène observée l'est (Fig. 7.3), et possède des composantes de FOURIER dans l'étoile, même si la scène observée n'en possède pas (Fig. 7.4).

De plus, il est illusoire de vouloir reconstruire $\widetilde {T}$ (et donc $T_o$ ) a son plus haut niveau de résolution, ses composantes de FOURIER aux hautes fréquences étant inaccessibles, de par la propriété de bande passante limitée des RISO, exprimée ici par l'action de l'opérateur $\mathbf{Z}^*$ . La température $T_r$ reconstruite par une simple transformée de FOURIER inverse :

$$T_r = \left\{\mathbf{U}^* \mathbf{Z}V \right\}\times \sqrt{1-\vert\vert\mathbf{\xi}\vert\vert^2} / \vert F(\mathbf{\xi})\vert^2$$ (7.5)

ne représente donc qu'une version basse résolution de $T_o$ , l'opérateur de reconstruction $\mathbf{U}^*\mathbf{Z}$ (bourrage de zéros + $\mathcal{TF}$  inverse) n'étant pas l'opérateur inverse de $\mathbf{Z}^*\mathbf{U}$ .

De plus, la division par le module du gain $F$ dans la relation (7.5) n'a de sens que pour un instrument idéal, c.-à-d.  si tous les gains sont identiques et si l'on observe aucun phénomène de décorrélation spatiale. L'utilisation de la transformée de FOURIER inverse comme opérateur de reconstruction pour un instrument réaliste possédant des antennes aux caractéristiques dispersées et subissant la décorrélation spatiale est par conséquent dépourvue de sens.

Figure 7.1: a), scène $T_o$ observée à son plus haut niveau de résolution, b), composantes de FOURIER et c), visibilités correspondantes.

Figure 7.2: a), version scène basses fréquences de la scène $T_o$ , b), composantes de FOURIERet c), visibilités correspondantes.

Figure 7.3: Visibilités mesurées pour une scène composée d'une distribution uniforme, de température égale à la température moyenne de $T_o$ .

Figure 7.4: a), version scène hautes fréquences de la scène $T_o$ , b), composantes de FOURIERet c), visibilités correspondantes.

7.2.2 La méthode CLEAN

La méthode CLEAN est utilisée en radio-astronomie pour traiter les données interférométriques issues, par exemple des réseaux du type ALMA. Elle a été développée en 1974 par HÖGBOM Hogbom. Il s'agit d'une méthode itérative de déconvolution adaptée à l'observation de champs comportant des sources ponctuelles (étoiles, galaxies ...) sur un fond plus ou moins bruité.

La première étape consiste à décomposer l'ensemble de l'image en un ensemble de composante ayant la forme d'une impulsion de DIRAC. Pour cela, on recherche le pixel d'intensité maximale dans le champ reconstruit et on soustrait à l'ensemble de la carte une fraction de la réponse impulsionnelle de l'instrument centrée sur ce maximum. Cette opération est renouvelée jusqu'à ce que le maximum dans le champ soit nul ou ramené au niveau du bruit de fond.

La seconde étape consiste à convoluer la carte des impulsions de DIRAC construite lors de l'étape précédente par une réponse impulsionnelle instrumentale synthétique ne comportant pas de lobes secondaires, par exemple une gaussienne dont la largeur est proche de celle du lobe principale de la véritable fonction de transfert de l'instrument. Finalement, il convient d'ajouter le résidu obtenu à la fin de la première étape. L'image ainsi reconstruite est nettoyée  de tout artefact indésirable.

L'équipe de traitement du signal de l'UPC a développé une méthode de reconstruction inspirée de cet algorithme Campsclean. L'avantage de cette technique est de ne pas exiger le stockage de grandes matrices, comme la matrice de modélisation, la taille du vecteur de plus grande dimension et celle des matrices sur lesquelles une FFT est appliquée étant fixées par le nombre de pixels dans l'image reconstruite. Le nombre d'itérations nécessaire à la convergence est faible, inférieur à 10, ce qui autorise la reconstruction en temps réel, au rythme de mesures des visibilités.

Toutefois, le stockage et la manipulation des matrices, compte tenue des avancées technologiques, n'est plus véritablement un problème, des ordinateurs équipés de la puissance et de la mémoire suffisante à ces opérations étant disponibles même auprès des particuliers. De plus, l'approche est en elle-même discutable. A aucun moment, le problème n'est régularisé : la solution obtenue par cette méthode dépend à la fois de l'initialisation et du nombre d'itérations. La carte des températures ainsi reconstruite correspond certainement à un minimum local et l'on pourrait atteindre une solution différente en augmentant le nombre d'itérations. Compte tenu des contraintes de temps, seul le premier minimum est atteint et donc la solution ne peut être que proche de l'initialisation.

Les aspects les plus problématiques résident sans doute dans le moyennage des gains d'antennes qu'implique l'utilisation de la $\mathcal{TF}$  et le moyennage des visibilités. En effet il a été montré dans le paragraphe précédent qu'il n'existait pas de relation de transformée de FOURIER entre les visibilités et la température de brillance, même modifiée. En outre, si le moyennage des gains d'antennes a un sens lorsque la dispersion des caractéristiques instrumentales est faible, on peut se poser la question dès lors que l'instrument est réaliste. De même, le moyennage des visibilités ne permet sans doute pas de tirer parti de toute l'information disponible lorsque les couples d'antennes définissant la même ligne de base ont des caractéristiques différentes.

Bien entendu, il aurait été important de pouvoir comparer cette méthodes avec les méthodes régularisées. Ce besoin a été exprimé par l'ESA qui a réuni au sein d'un groupe d'étude sur des méthodes de reconstruction alternatives, les équipes du DLR et la notre. Le but était de faire le point sur les caractéristiques des méthodes développées et de les comparer à la méthode CLEAN implémentée dans le SEPS SMOS End-to-end Performance Simulator. Cependant, il n'a pour l'instant pas été possible de réunir un consensus sur la modélisation de l'instrument et la simulation des visibilités. Privé d'un socle commun indispensable pour une comparaison sérieuse, il n'a pas été possible de comparer les performances des méthodes régularisées avec celles développées par l'UPC et le DLR. J'ai participé activement à la réécriture des routines du SEPS en charge de la simulation des visibilités et de la modélisation de l'instrument ainsi qu'à l'adaptation des méthodes de régularisation dans le but d'une intégration dans le SEPS. Des travaux sont actuellement en cours pour parvenir a une solution.

7.2.3 L'algorithme de calibration par points chauds

Le DLR a développé plusieurs méthodes de reconstruction, certaines basées sur la méthode CLEAN DLR. La méthode succinctement présentée ici à l'avantage de ne pas nécessiter une caractérisation précise de l'instrument. Le but est de construire point par point une matrice $\widehat {\mathcal{W}}$ , dont l'inversion fournit un opérateur permettant directement la reconstruction d'une carte de température de brillance :

$$T = \widehat {\mathcal{W}}^{-1} V$$ (7.6)

La matrice $\widehat {\mathcal{W}}$ est construite à partir de l'observation d'un point chaud, tel le soleil ou la lune, dont la température de brillance est parfaitement connue et dont la résolution angulaire est inférieure ou égale à la résolution angulaire de l'instrument. Pour une position donnée de ce point chaud dans le champ de vue de l'instrument, la mesure des visibilités fournit directement la réponse impulsionnelle instrumentale, toute imperfection comprise, pour le pixel du champ reconstruit correspondant, soit une colonne de la matrice $\widehat {\mathcal{W}}$ . Différentes orientations du réseau d'antennes vont permettre de faire parcourir au point chaud l'ensemble du champ de vue et donc de construire $\widehat {\mathcal{W}}$ colonne par colonne.

L'avantage de cette méthode réside dans la prise en compte directe des possibles imperfections instrumentales et dans l'absence de processus itératif. Même si l'inversion de la matrice est chronophage, elle n'est effectuée que lors des étapes de calibration, lorsque la dérive des caractéristiques instrumentales est devenue critique.

Cependant, la phase de construction par un unique point chaud est technologiquement difficile à envisager dans le cadre d'une mission spatiale, la succession de réorientations et de stabilisations de l'instrument étant difficilement réalisable et surtout très coûteuse en énergie. Des études sont donc en cours pour appliquer cette méthode à des scènes test étendues pour lesquelles la distribution des températures de brillance est parfaitement connue.

Biographie(s) HADAMARD, Jacques Salomon
(8 décembre 1865, Versailles, France - 17 Octobre 1963, Paris, France)hadamard.eps

Agé de trois ans, il suit ses parents, tous deux enseignants, à Paris, son père prenant un poste au lycée Charlemagne. Hadamard commence ici sa scolarité, pour la finir au lycée Louis-le-Grand où son père est muté. En 1883, il obtient un baccalauréat ès lettres et ès sciences. Il est premier prix du Concours Général en algèbre et en mécanique.
En 1884, il termine premier des concours d'entrée de l'Ecole Polytechnique et de l'Ecole Normale Supérieure, optant pour cette dernière. Il y débute ses recherches sur l'estimation du déterminant généré par les coefficients d'une série en puissance. En 1892, il soutient une thèse sur les fonctions de Taylor. Son travail sur les fonctions complexes est un des premiers à aborder une théorie générale des fonctions analytiques.
Il passe quatre ans à Bordeaux à partir de 1892. Il publie durant cette période 29 articles, ce nombre impressionnant étant dépassé par la qualité de ces travaux et l'étendue des sujets abordés. Au cours de sa carrière, il sera successivement et parfois dans le même temps, professeur de la faculté des sciences de la Sorbonne, du Collège de France, de l'Ecole Polytechnique et de l'Ecole Centrale.
Outre ses travaux sur les nombres premiers, les propriétés des trajectoires dynamiques, les équations aux dérivées partielles, l'élasticité, l'optique géométrique, l'hydrodynamique, il publie des traités fondateurs pour l'enseignement des mathématiques en France, comme Leçons de géométrie élémentaire.
Engagé politiquement, il prend une part active dans la défense d'Alfred Dreyfus et participe à sa réhabilitation. Ayant perdu trois fils durant les deux guerres mondiales, il milita activement pour la paix. [bibli]