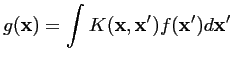7.1 Problème direct - Problème inverse

Le problème direct a clairement été exposé au cours des parties précédentes. La distribution de températures de brillance sur Terre est observée par les antennes du réseau interférométrique. Le champ électromagnétique incident se propageant dans un espace libre est transformé en un signal se propageant dans la ligne de transmission. A la sortie de la chaîne de réception, la corrélation des signaux permet d'accéder à un échantillonnage de la fonction de cohérence spatiale de la scène observée.

Le problème inverse consiste alors à estimer une carte de distribution de températures de brillance expliquant au mieux, selon des critères qui restent à préciser, les mesures instrumentales et ce, à partir de la modélisation fournie par la relation de VAN CITTERT-ZERNIKE (relation 3.38).

Cette relation intégrale est dite de FREDHOLM de première espèce, une formulation classique dans le traitement de l'image :

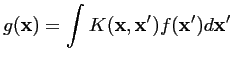$$g(\mathbf{x}) = \int K(\mathbf{x},\mathbf{x}') f(\mathbf{x}') d\mathbf{x}'$$ (7.1)

En imagerie par synthèse d'ouverture, le noyau $K$ la fonction de modélisation de l'instrument et conduit à une relation linéaire entre les données $g$ , les visibilités, et les inconnues $f$ , la distribution de températures de brillance.

Dans sa version discrète, le système linéaire à résoudre est (voir relation (4.41)) formulé ainsi :

$$\mathbf{G}T = V$$ (7.2)

La solution de ce système minimise aussi le critère de moindres carrés :

$$\min_{T \in E} \vert\vert V - \mathbf{G}T \vert\vert ^2_F,$$ (7.3)

et est aussi solution de l'équation normale :

$$\mathbf{G}^* \mathbf{G}T = \mathbf{G}^* V$$ (7.4)

Ce type de problème est en général mal posé. Selon la définition d'HADAMARD Hadamard, un problème est bien posé lorsque ces trois conditions sont remplies :

1. il existe une solution

2. la solution est unique

3. la solution est une fonction continue des données, c.-à-d. une faible perturbation des données conduit à une faible perturbation de la solution.

Or, ici, le problème est sous-contraint, le nombre d'inconnues, les $N^2$ pixels de la scène échantillonnée, étant inférieur au nombre $N_b$ de mesures instrumentales. Le problème 7.4, et par conséquent les problèmes 7.3 et 7.2, possèdent alors une infinité de solutions, la matrice carrée $(\mathbf{G}^* \mathbf{G})$ étant singulière. Ce problème est donc bien mal posé.

La cause physique de cette perte d'information entre le domaine spatial et le domaine de FOURIER trouve sa source dans une caractéristique importante des radiomètres imageurs à synthèse d'ouverture : ce sont des instruments à bande passante limitée. Leurs dimensions limitées ne permettent d'avoir accès qu'aux fréquences confinées dans $H$ et non pas à l'ensemble des fréquences formant la grille d'échantillonnage dans le domaine de FOURIER.

On peut alors opposer deux approches de la résolution d'un tel problème.

D'une part, les méthodes présentées brièvement dans la section suivante, la première développée par l'équipe traitement du signal de l'Université Polytechnique de Catalogne (UPC), la seconde par le Deutsches Zentrum für Luft- und Raumfahrt (DLR), isolent une solution parmi l'infinité possible sans modifier le problème à résoudre.

D'autre part, la démarche adoptée dans cette situation, courante dans le cadre général de la reconstruction d'image Bertero, consiste à régulariser le problème à résoudre, c.-à-d. à apporter une information supplémentaire, sous quelques formes que ce soit, permettant de choisir une solution particulière parmi l'infinité possible : avant toute chose, on s'assure donc de l'existence et de l'unicité de la solution.

Dans le chapitre suivant, je décrirai précisément trois régularisations distinctes conduisant à trois différentes méthodes de reconstruction d'image pour les radiomètres à synthèse d'ouverture, ayant participé activement au développement et à la mise en oeuvre de deux d'entre elles.