8.3 Régularisation physique dite méthode à bande passante limitée

Jusqu'à présent, nous nous sommes contraints à estimer directement les valeurs des $N^2$ pixels composant la carte des températures de brillance à partir des seules $N_b$ visibilités mesurées.

E. Anterrieu [#!EricMatres!#] a proposé d'introduire, dès la formulation du problème inverse à résoudre, une information a priori sur le fonctionnement du radiomètre à synthèse d'ouverture. Comme ces derniers sont des instruments à bande passante limitée, il est illusoire de vouloir estimer des cartes à une résolution supérieure à celle imposée par les limites de la bande passante.

Or, si l'on impose à la solution du problème d'être à bande passante limitée, il est équivalent de vouloir trouver les valeurs des $N^2$ pixels dans le domaine spatial ou les $N_f$ composantes de FOURIER contenues dans $H$ . Il suffit alors de remarquer que, grâce aux mesures redondantes, on dispose de plus de données interférométriques que de fréquences à l'intérieur de la bande passante, pour comprendre que le problème inverse à résoudre est alors bien posé.

Il s'agit donc de trouver le minimum du critère quadratique :

$$\min_{T \in E} \vert\vert V-\mathbf{G}T \vert\vert _F^2$$ (8.15)

sous la contrainte

$$(\mathbf{I}- \mathbf{P}_H)T=0$$ (8.16)

où $\mathbf{P}_H$ est l'opérateur de projection dans le sous-espace $\mathcal{E}$ des fonctions à bande passante limitée à $H$ . En remarquant que les composantes de FOURIER  $\mathcal{T}$ contenues dans la bande passante sont liées à la carte des température de brillance par

$$T = \mathbf{U}^* \mathbf{Z}\mathcal{T},$$ (8.17)

les relations (8.15) et (8.16) sont résumées par le critère de moindres carrés :

$$\min_{\mathcal{T} \in \mathcal{E}} \vert\vert V-\mathbf{A}\mathcal{T} \vert\vert _F^2$$ (8.18)

où $\mathbf{A}= \mathbf{G}\mathbf{U}^* \mathbf{Z}$ est appelée matrice résolvante. La solution du système sur-contraint (8.18) est aussi solution de l'équation normale

$$\mathbf{A}^* \mathbf{A}\mathcal{T}= \mathbf{A}^* V$$ (8.19)

Les composantes de FOURIER  $\mathcal{T}_r$ sont reconstruites à l'aide de $\mathbf{A}^+$ , l'inverse généralisé dit de MOORE-PENROSE de la matrice $\mathbf{A}$ :

$$\mathcal{T}_r = {\mathbf{A}}^+ V$$ (8.20)

$$\textrm{avec}~{\mathbf{A}}^+ = \mathbf{A}^*(\mathbf{A}\mathbf{A}^*)^{-1}$$ (8.21)

La carte des températures à bande passante limitée $T_r$ est directement déduite de $\mathcal{T}_r$ grâce à la relation (8.17) :

$$T_r = \mathbf{U}^* \mathbf{Z}\mathbf{A}^+ V$$ (8.22)

Contrairement aux solutions précédentes, qui ont une interprétation mathématique, cette solution a un sens physique clair : il s'agit de la carte des température de brillance qui aurait été reconstruite si les visibilités avaient été fournies par un instrument idéal à la résolution imposée par la bande passante.

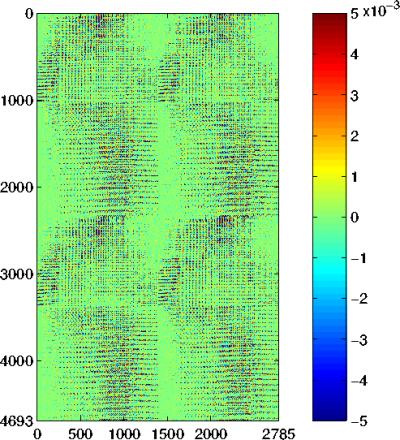
La figure 8.1 montre la matrice $\mathbf{A}$ correspondant à un instrument réaliste de type MIRAS. Elle est réelle, puisque construite d'après la matrice $\mathbf{G}$ réelle. Les $N_b$ premières lignes sont la partie réelle de la contribution aux visibilités mesurées d'un dirac en un point de la bande passante limitée, les $Nb-1$ suivante, la partie imaginaire de cette contribution. Pour construire les $N_f$ premières colonnes, on considère un dirac réel, puis imaginaire pour les $N_f+1$ suivantes.

Figure 8.1: La matrice résolvante  $\mathbf{A}$ pour un instrument réaliste de type MIRAS. Notons que des éléments de cette matrice ont une valeur de quelques unités (l'échelle de couleur a été choisie ici pour un meilleure contraste).