



Next: 8.3 Régularisation physique dite
Up: 8. Méthodes de reconstruction
Previous: 8.1 Régularisation mathématique
Une autre approche standard en reconstruction d'image
consiste à minimiser dans un même temps l'écart aux données
et la norme de la solution Tik :
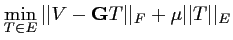 |
(8.12) |
où 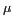 est un paramètre de LAGRANGE pondérant
l'importance accordée à la minimisation de la norme de la solution.
Pour
est un paramètre de LAGRANGE pondérant
l'importance accordée à la minimisation de la norme de la solution.
Pour 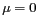 , on retrouve le critère de moindres carrés (7.3).
Le minimum de la fonctionnelle quadratique (8.12) est aussi
solution de l'équation d'Euler :
, on retrouve le critère de moindres carrés (7.3).
Le minimum de la fonctionnelle quadratique (8.12) est aussi
solution de l'équation d'Euler :
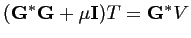 |
(8.13) |
La perturbation de l'opérateur
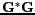 par la matrice diagonale
par la matrice diagonale 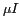 permet de calculer l'opérateur
permet de calculer l'opérateur
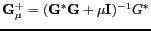 dont propriétés d'amplification du bruit sur les données sont contrôlées
par
dont propriétés d'amplification du bruit sur les données sont contrôlées
par 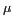 . Il existe alors une valeur optimale de
. Il existe alors une valeur optimale de 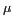 pour laquelle un compromis optimal est atteint entre l'erreur de
reconstruction et l'amplification des bruits sur les données. La solution
de 8.12 est :
pour laquelle un compromis optimal est atteint entre l'erreur de
reconstruction et l'amplification des bruits sur les données. La solution
de 8.12 est :
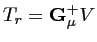 |
(8.14) |
où 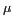 est un paramètre de régularisation.
est un paramètre de régularisation.




Next: 8.3 Régularisation physique dite
Up: 8. Méthodes de reconstruction
Previous: 8.1 Régularisation mathématique
nous
2005-03-31