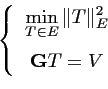 |
(8.1) |
Une approche Tanner consiste à trouver la solution de norme minimale parmi les solutions de (7.2), en résolvant le problème d'optimisation avec contrainte :
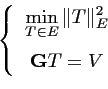 |
(8.1) |
| (8.2) |
| (8.3) |
Or, certaines lignes de
![]() sont au mieux numériquement très proches
voire identiques puisque deux couples d'antennes différents
peuvent définir la même
ligne de base et ainsi fournir deux mesures différentes de
la fonction de cohérence spatiale à la même fréquence.
sont au mieux numériquement très proches
voire identiques puisque deux couples d'antennes différents
peuvent définir la même
ligne de base et ainsi fournir deux mesures différentes de
la fonction de cohérence spatiale à la même fréquence.
Ainsi, à un instrument idéal correspond une matrice
![]() dont
certaines lignes sont identiques et dont le rang est alors
égal à
dont
certaines lignes sont identiques et dont le rang est alors
égal à ![]() , où
, où ![]() est le nombre de fréquences dans
la bande passante. Pour un instrument réaliste, même si la
matrice est rigoureusement de rang plein, les lignes
correspondant aux visibilités redondantes sont numériquement
très proches.
est le nombre de fréquences dans
la bande passante. Pour un instrument réaliste, même si la
matrice est rigoureusement de rang plein, les lignes
correspondant aux visibilités redondantes sont numériquement
très proches.
Rang, SVD et conditionnement d'une matrice
Le rang ![]() d'une matrice
d'une matrice ![]() (
(![]() ) avec
) avec ![]() est le nombre
de lignes linéairement indépendantes. Si
est le nombre
de lignes linéairement indépendantes. Si ![]() , la matrice
est dite de rang plein. Si
, la matrice
est dite de rang plein. Si ![]() , la matrice est dite de
rang déficient.
, la matrice est dite de
rang déficient.
La décomposition en valeurs singulières d'une matrice ![]() (
(![]() ,
,![]() ) consiste à décomposer la matrice en un produit de trois matrices
) consiste à décomposer la matrice en un produit de trois matrices
![]() (
(![]() ),
), ![]() (
(![]() ) et
) et ![]() (
(![]() ) :
) :
| (8.4) |
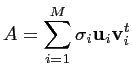 |
(8.5) |
Le rang d'un matrice est aussi donné par le nombre de valeurs singulières non nulles.
Le conditionnement d'une matrice est donné par le rapport
entre la plus petite et la plus grande de ses valeurs
singulières :
| (8.6) |
Pour un instrument réaliste, le facteur d'amplification du
bruit sur les données par l'opérateur
![]() est
alors très grand, un majorant de ce facteur étant
donné par le conditionnement de la matrice de modélisation :
est
alors très grand, un majorant de ce facteur étant
donné par le conditionnement de la matrice de modélisation :
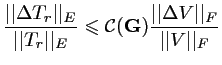 |
(8.7) |
Or, ceci est en contradiction avec l'une des conditions données par HADAMARD et le problème reste mal posé. En effet, un conditionnement de la matrice élevé implique qu'une faible perturbation des données va conduire à une grande perturbation de la solution.
Une solution pour améliorer le conditionnement de
![]() consiste alors à écarter certaines lignes parmi celles qui
sont redondantes ou encore à les moyenner. Le
moyennage est bien sûr préférable mais une conséquence de cette
situation est la diminution du rapport entre la quantité d'information et
le nombre d'inconnues d'un système linéaire qui est déjà
sous-contraint.
consiste alors à écarter certaines lignes parmi celles qui
sont redondantes ou encore à les moyenner. Le
moyennage est bien sûr préférable mais une conséquence de cette
situation est la diminution du rapport entre la quantité d'information et
le nombre d'inconnues d'un système linéaire qui est déjà
sous-contraint.
Une solution plus robuste consiste à étudier la répartition
des valeurs singulières de
![]() EricMatresbrunoComp.
EricMatresbrunoComp.
L'opérateur
![]() peut être calculé grâce à une
décomposition en valeur singulière de
peut être calculé grâce à une
décomposition en valeur singulière de
![]() . Si
. Si
![]() adopte la décomposition suivante,
adopte la décomposition suivante,
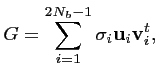 |
(8.8) |
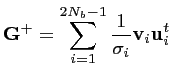 |
(8.9) |
Puisque les valeurs singulières les plus petites sont
responsables de l'amplification du bruit, une régularisation
possible du problème inverse consiste à construire un
opérateur
![]() en ne conservant que les
en ne conservant que les ![]() plus
grandes valeurs propres (chapt. 3 et 5 dans Hansen) :
plus
grandes valeurs propres (chapt. 3 et 5 dans Hansen) :
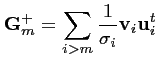 |
(8.10) |
L'information perdue dans les hautes fréquences est ici
comblée par une information de nature mathématique. La
solution de (![]() ) par la régularisation dite
mathématique est alors :
) par la régularisation dite
mathématique est alors :