Contenu

• 8.4.1 Valeurs optimales pour les paramètres de régularisation
• 8.4.2 Point de vue informatique

8.4 Comparaison des méthodes de régularisation

Outre les performances en terme d'erreur de reconstruction qui seront abordées dans les sections suivantes, il est d'ores et déjà possible d'émettre quelques remarques sur les particularités des méthodes présentées ci-dessus.

8.4.1 Valeurs optimales pour les paramètres de régularisation

La détermination de la valeur optimale pour un paramètre de régularisation, notamment pour l'approche de TIKHONOV, peut se faire en étudiant la courbe en L , construite en reportant l'écart aux données $\vert\vert V-\mathbf{G}T_r \vert\vert$ en fonction de la norme de la solution $\vert\vert T_r \vert\vert$ .

Figure 8.2: Variation de $\vert\vert V-\mathbf{G}T_r \vert\vert _F$ avec $\vert\vert T_r \vert\vert _E$ pour la solution de TIKHONOV() avec $10^{-8}\leqslant \mu \leqslant 10^{-1}$ , pour la régularisation mathématique () avec $1700\leqslant m \leqslant 4700$ et pour la solution à bande passante limitée (). En haut à gauche, zoom sur le creux de la courbe en L.

Le paramètre optimal, du point de vue du compromis entre l'écart aux données et la norme de la solution, est alors trouvé au creux de la courbe ainsi obtenue. La figure montre une telle courbe pour un instrument réaliste de type MIRAS et pour la scène reportée sur la figure .

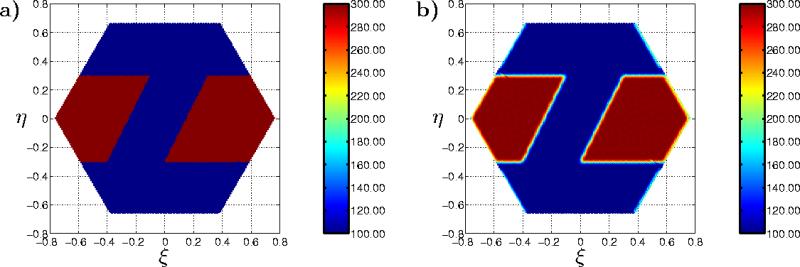
Comme l'illustre la figure , la valeur du paramètre de régularisation joue sur la qualité de reconstruction. Selon le contexte de la reconstruction et notamment le niveau de bruit sur les données, il est alors possible d'imposer une plus ou moins grande résolution spatiale en sur- ou sous- régularisant le problème à résoudre.

Figure 8.3: a) scène observée à son plus haut niveau de résolution et b) au niveau de résolution de l'instrument et apodisée par la fenêtre de HANNING.

L'avantage de l'approche de TIKHONOV est de pouvoir faire varier continûment la valeur de $\mu$ . Cependant, cette dernière est directement liée à la scène observée et doit être recalculée pour chaque jeu de mesures.

Dans le cas de la décomposition en valeurs singulières tronquée, si le nombre de valeurs singulières écartées $m$ joue effectivement le rôle d'un facteur de régularisation (voir Fig. 8.2 et 8.7), sa valeur optimale, du point de vue du compromis entre erreur de reconstruction et facteur d'amplification, est uniquement fixée par les dimensions du problème et ne dépend donc pas de la scène observée.

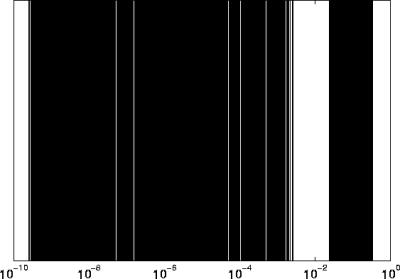
En effet, les valeurs singulières de la matrice de modélisation $\mathbf{G}$ sont clairement réparties en deux groupes (voir Fig. 8.4). Un premier, regroupé autour de 1, compte autant de valeurs singulières que de fréquences dans la bande passante tandis que le second, regroupé autour de valeurs nettement inférieures à 1, compte autant de valeurs singulières que de redondances. Ce sont ces dernières qui sont responsables de l'amplification du bruit et il est donc naturel de les écarter. Ainsi, la valeur $m=(2N_b-1)-(2N_f-1)$ ($m=1908$ pour MIRAS), correspondant aux nombres de redondances, est optimale, comme le confirme l'étude de la courbe en L.

Figure 8.4: Valeurs singulières de la matrice $\mathbf{G}$ : elles sont clairement réparties en deux groupes (en noir).

De l'étude de la courbe en L de la régularisation mathématique, il ressort que le nombre de degrés de liberté du problème à résoudre est plutôt lié au nombre de fréquences dans la bande passante qu'au nombre de visibilité. Cette remarque renforce la pertinence de la reformulation du problème inverse pour la méthode à bande passante limitée. Cette dernière ne dépend d'aucun paramètre de régularisation mais la solution à bande passante limitée est proche des solutions obtenues avec le paramètre optimal des méthodes précédentes (voir Fig. 8.2 et Fig. 8.5).

Sans doute les avantages les plus importants de cette méthode découlent-ils du fait de résoudre le problème dans le domaine de FOURIER et de la nature à bande passante limitée de la solution reconstruite. Ainsi, l'apodisation des solutions obtenues par des méthodes résolvant le problème dans le domaine spatial demande l'application d'une FFT directe, de l'opérateur $\mathbf{Z}^*$ , afin de ne garder que les composantes aux fréquences contenues dans la bande passante, l'application de la fenêtre à l'aide de $\widehat {\mathbf{W}}$ , celle de l'opérateur $\mathbf{Z}$ de bourrage de zéro et enfin celle d'une FFT inverse :

$$\mathcal{T}_{rw} = \mathbf{U}^* \mathbf{Z}\widehat {\mathbf{W}} \mathbf{Z}^* \mathbf{U}T_{r}$$ (8.23)

L'opérateur $\widehat {\mathbf{W}}$ est une matrice diagonale contenant les coefficients de la fenêtre choisie.

On peut s'étonner d'être obligé de diminuer la résolution de la solution initialement obtenue en coupant les hautes fréquences et s'interroger sur la signification physique d'une solution à résolution plus grande que celle de l'instrument.

Dans le cas de la solution de la régularisation physique, l'apodisation se fait directement sur le résultat de l'application de l'opérateur $\mathbf{A}^+$ sur les données, et le retour au domaine direct se fait grâce à $\mathbf{Z}$ et $\mathbf{U}^*$ :

$$\mathcal{T}_{rw} = \mathbf{U}^* \mathbf{Z}\widehat {W} \mathcal{T}_{r}$$ (8.24)

De plus, la solution étant à bande passante limitée, l'interpolation de la solution sur une grille régulière dans le référentiel terrestre est facilitée.

Figure 8.5: Solution à bande passante limitée.

Figure 8.6: Cartes de température reconstruites à l'aide de la régularisation de TIKHONOV: a)  $\mu=3.7\times10^{-7}$  (optimal), b)  $\mu=10^{-3}$  (sur-régularisation), c)  $\mu=10^{-8}$  (sous-régularisation).

Figure 8.7: Cartes de température reconstruites à l'aide de la régularisation mathématique : a) $m=1908$  (optimal), b) $m=2900$  (sur-régularisation), c) $m=1700$  (sous-régularisation).

8.4.2 Point de vue informatique

Une partie de mon travail de thèse à consisté à implémenter, pour des instruments aux dimensions réalistes, la méthode à bande passante limitée déjà existante, ainsi que les autres méthodes nous avons développés, la régularisation mathématique et l'approche de TIKHONOV.

Afin de faciliter le calcul de la matrice de modélisation, notamment pour la simulation de l'instrument MIRAS, les codes de calcul en FORTRAN ont été parallélisées à l'aide de la librairie d'instruction $OpenMP$ pour pouvoir être portés sur deux architectures parallèles différentes : une architecture NUMA-cc (machine SGI O3000) dite à mémoire virtuellement partagée et une architecture à mémoire distribuée (machine COMPAQ MATHEND000#-SERVER SC45). Selon l'architecture, les version parallélisées des librairies scientifiques SCI (SGI O3000) CXML (COMPAQ MATHEND000#-SERVER SC 45) ont été utilisées.

Avant tout, il est utile de remarquer qu'il n'est pas nécessaire de procéder au calcul et au stockage des opérateurs de reconstruction dans le cas des méthodes de TIKHONOV et à bande passante limitée. Il existe de multiples approches permettant de minimiser les critères de moindres carrés (8.12) et (8.15). Une fois le problème régularisé, lorsque l'existence d'une unique solution est assurée, des méthodes itératives de type gradients conjugués peuvent être employées avec la certitude de leur convergence. L'avantage est bien entendu de limiter l'espace mémoire nécessaire à l'estimation de la solution.

Cependant, les méthodes matricielles, si elles sont plus contraignantes du point de vue du matériel informatique, offrent l'avantage de pouvoir procéder à de multiples reconstructions simultanées, au prix d'un produit matrice-matrice, opération facilement parallélisable. Il faut aussi noter que le calcul de ces opérateurs, tous basés sur l'utilisation de la matrice de modélisation, n'est nécessaire qu'à chaque étape de calibration de l'instrument. Les technologies actuellement disponibles, tant matérielles qu'algorithmiques, permettent d'assurer la validité de l'implémentation de ces méthodes compte tenu des contraintes de temps imposées par le rythme de l'acquisition des données (1.5s) et celui de la calibration (1 orbite pour MIRAS, soit environ 1h).

Les opérateurs $\mathbf{G}_m^+$ et $\mathbf{G}_\mu^+$ sont des opérateurs de la dimension de l'opérateur de modélisation. L'implémentation pratique de leur calcul demande donc des ressources importantes. Le tableau 8.1 résume les contraintes informatiques pour la régularisation mathématique et la méthode à bande passante limitée.

L'opérateur $\mathbf{G}_m^+$ est calculé d'après la décomposition en valeurs singulières de $\mathbf{G}$ opérée grâce à la routine DGESVD de la libraire scientifique LAPACK. En plus du stockage de la matrice $\mathbf{G}$ , écrasée par la matrice $V$ à la fin du calcul, elle nécessite le stockage de la matrice $U$ contenant les vecteurs singuliers à gauche.

La méthode à bande passante limitée offre de nombreux avantages du point de vue de l'implémentation pratique. Les dimensions du nouveau problème à résoudre sont plus petites que celles du problème initial : ici, le nombre de colonnes de la matrice est lié au nombre de fréquences dans la bande passante, alors qu'il est lié au nombre de pixels de la grille d'échantillonnage pour la matrice $\mathbf{G}$ , ce qui conduit à diviser la taille de l'opérateur de reconstruction par 6 pour MIRAS et par 7 pour HUT2D. De même, il est possible de ne stocker que les composantes de FOURIER à l'intérieur de la bande passante, et non les $N^2$ pixels de la solution dans le domaine spatial. Pour les simulations réalisées dans ce document, il a été choisi de calculer l'inverse généralisé de $\mathbf{A}$ grâce à une décomposition en valeurs singulières. Le calcul de $\mathbf{A}^+$ prend alors 3 fois moins de temps pour MIRAS, 20 fois moins pour HUT2D, que le calcul de $\mathbf{G}^+$ .

Table 8.1: Tailles des opérateurs et temps de calcul pour la régularisation mathématique et la méthode à bande passante limitée (instrument type MIRAS). Les tailles sont données pour un stockage en double précision et les temps de calcul sont mesurés sur un COMPAQ MATHEND000#-SERVER SC 45 en utilisant une parallélisation OpenMP et la bibliothèque de calcul constructeur CXML parallélisée sur 4 processeurs.

			Temps de calcul
	Dimensions	Taille	Matrice	Opérateur de reconstruction (SVD+inversion)	100 reconstructions
$\mathbf{G}$	$(2N_b-1)\times N^2$ $= 4693\times 16384$	586.6 Mo	15 s	90+3 min	3 min
$\mathbf{A}$	$(2N_b-1)\times(2N_f-1)$ $= 4693\times 2785$	99.7 Mo	10 min	30+0.5 min	< 5 s

En conclusion, la comparaison des méthodes régularisées à l'aide de la courbe en L offre un nouvel éclairage sur leurs caractéristiques respectives. La régularisation de TIKHONOV, pour la première fois appliquée à la reconstruction d'image pour les radiomètres à synthèse d'ouverture, a permis de redéfinir le nombre de valeurs singulières écartées la régularisation mathématique comme un paramètre de régularisation aux même titre que le paramètre de TIKHONOV. Le choix de la valeur optimale pour le paramètre $m$ comme étant le nombre de redondances est confirmée non seulement par l'étude du spectre des valeurs singulières mais aussi par l'étude de la courbe en L. Il est alors possible de faire varier ce paramètre et de sur- ou sous-régulariser le problème à résoudre, changeant du même coup la sensibilité de la solution aux bruits sur les données et la qualité de l'accord aux données.

La méthode à bande passant limitée, si elle ne dépend pas d'un paramètre de régularisation, fournit non seulement une solution proche des solutions obtenues avec la valeur optimale du paramètre de régularisation des autres méthodes, mais possède en outre des avantages liés à la propriété imposée à cette solution. L'apodisation et l'interpolation de la carte de température de brillance estimée peut se faire dans le même temps que le passage du domaine de FOURIERdans lequel se fait la résolution du problème vers le domaine spatial de la solution recherchée. De plus, la reformulation du problème conduit à diminuer les dimensions de l'opérateur de reconstruction (comparé aux autres méthodes), facilitant ainsi la mise en oeuvre informatique et diminuant les temps de calcul, ce qui représente un avantage compte tenu des contraintes sur le traitement en temps réel des données dans le cadre d'une mission spatiale.